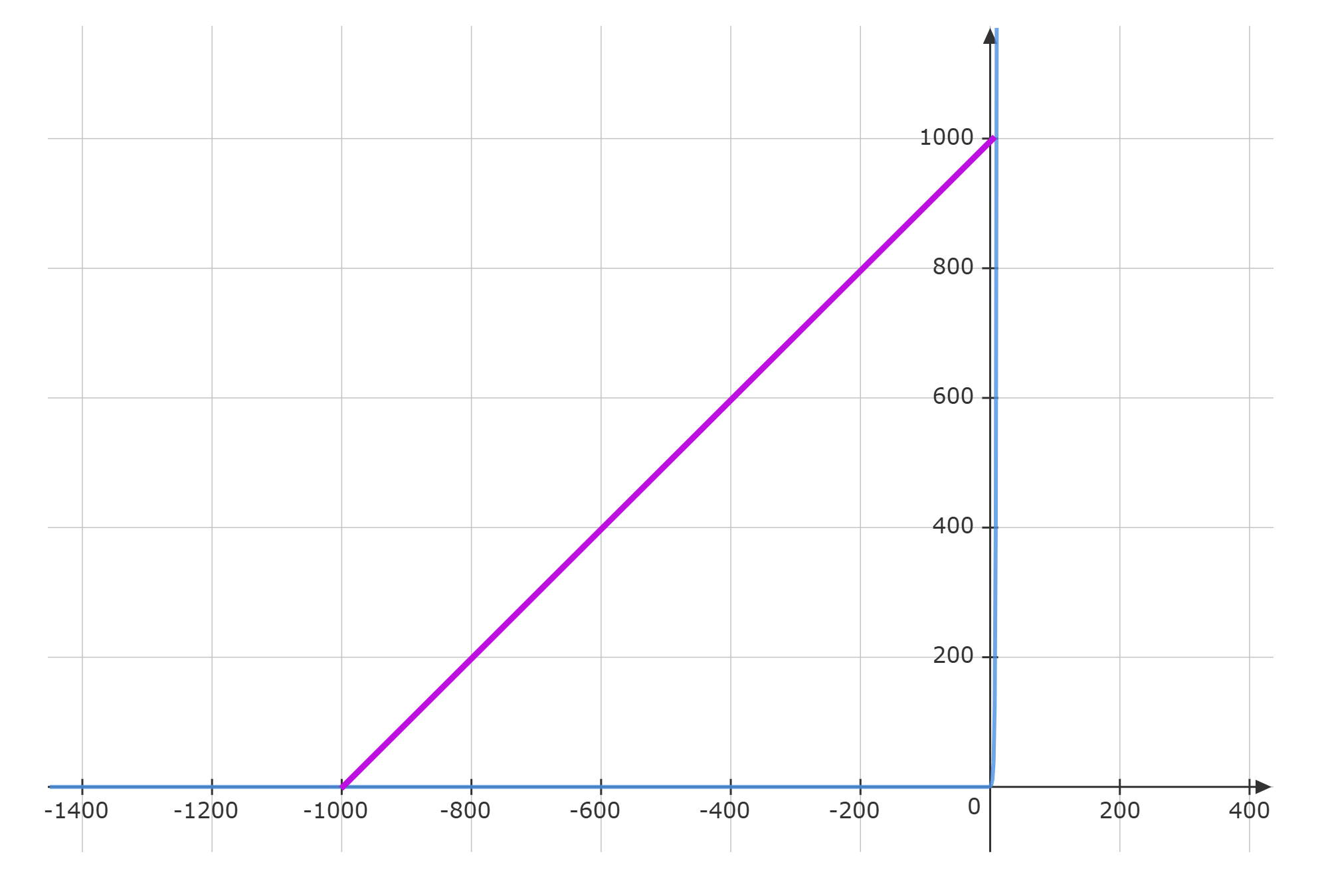
Gegeben ist die Funktion: für die ganzen Zahlen
Diskutiere den Satz: "Der Graph der Exponentialfunktion ergibt einen rechten Winkel".
Bestimme die kleinste Zahl , so dass für alle gilt: .
Wie ändert sich die Antwort in b), wenn die rechte Seite () mit multipliziert wird, also die Ungleichung betrachtet wird?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?