Aufgaben zum Thema Potenzen und Polynome

1
Berechne $2^{n}$ für $n = 0 \dots 20$ .
Für größere Zweierpotenzen ist die Faustregel " $2^{10}$ oder $1000$ - das ist doch praktisch dasselbe" nützlich. Gib damit Näherungen für $2^{32}$ und $2^{64}$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen und Polynome
Hier die Ergebnisse für $2^{n}$ für $n \in {0, \dots, 20}$ :
$\begin{array}{l} 2^{0} = 1 \\ 2^{1} = 2 \\ 2^{2} = 4 \\ 2^{3} = 8 \\ 2^{4} = 16 \\ 2^{5} = 32 \\ 2^{6} = 64 \\ 2^{7} = 128 \\ 2^{8} = 256 \\ 2^{9} = 512 \\ 2^{10} = 1024 \\ 2^{11} = 2048 \\ 2^{12} = 4096 \\ 2^{13} = 8192 \\ 2^{14} = 16384 \\ 2^{15} = 32768 \\ 2^{16} = 65536 \\ 2^{17} = 131072 \\ 2^{18} = 262144 \\ 2^{19} = 524288 \\ 2^{20} = 1048576 \end{array}$
Wenn du nun die Näherung $2^{10} \approx 1000$ für $2^{32}$ und $2^{64}$ anwendest, erhältst du:
$2^{32} = 2^{10} \cdot 2^{10} \cdot 2^{10} \cdot 2^{2} \approx 1000 \cdot 1000 \cdot 1000 \cdot 4 = 4000000000 = 4 \cdot 10^{9}$
Im Vergleich dazu der richtige Wert:
$2^{32} = 4294967296$
Und:
$2^{64} = 2^{32} \cdot 2^{32} \approx 4 \cdot 10^{9} \cdot 4 \cdot 10^{9} = 16 \cdot 10^{18} = 1,6 \cdot 10^{19}$
Der richtige Wert ohne Näherung ist:
$2^{64} = 18446744073709551616 \approx 1,8447 \cdot 10^{19}$
2
Wie viele verschiedene Zustände kannst du mit $n$ Bits darstellen? Speziell: Wenn du ganze Zahlen (bei $0$ beginnend) in $32$ Bit speicherst, wie weit kannst du damit zählen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen und Polynome
Bezeichne mit $z (n)$ die Anzahl von verschiedenen Zuständen bei $n$ Bits. Dann gilt: Ein Bit hat zwei verschiedene Zustände, nämlich $0$ und $1$ . Also gilt $z (1) = 2$ . Wenn du ein weiteres Bit hinzufügst, erhältst du doppelt so viele Zustände wie vorher, da für jeden bisherigen Zustand das neue Bit entweder $0$ oder $1$ kann.
Du erkennst: Der Wert $z (n)$ ergibt sich aus der rekursiven Definition von $2^{n}$ , daher gilt: $z (n) = 2^{n}$
Wenn du nun speziell den Fall von 32 Bits betrachtest, so kannst du $z (32) = 2^{32}$ Zustände darstellen. Die größte Zahl ist allerdings $z (32) - 1 = 4294967295$ , da du mit $0$ anfängst zu zählen.
3
Berechne $(\sum_{i = 0}^{n} x^{i}) \cdot (x - 1)$ und stelle damit eine geschlossene Formel (d.h. ohne Summenzeichen) zur Berechnung von $\sum_{i = 0}^{n} x^{i}$ für $x \neq 1$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen und Polynome
Um den geforderten Term zu berechnen, multiplizierst du erst aus:
$\sum_{i = 0}^{n} x^{i} (x - 1) = \sum_{i = 1}^{n + 1} x^{i} - \sum_{i = 0}^{n} x^{i}$
Du erkennst, dass sich Großteil der Summen überschneidet:
$\sum_{i = 1}^{n + 1} x^{i} - \sum_{i = 0}^{n} x^{i} = x^{n + 1} + (\sum_{i = 1}^{n} x^{i} - \sum_{i = 1}^{n} x^{i}) - x^{0}$
Wenn du diesen entfernst, bleibt:
$x^{n + 1} + (\sum_{i = 1}^{n} x^{i} - \sum_{i = 1}^{n} x^{i}) - x^{0} = x^{n + 1} + 0 - 1 = x^{n + 1} - 1$
Nun formst du um:
$\sum_{i = 0}^{n} x^{i} (x - 1) = x^{n + 1} - 1$
$\sum_{i = 0}^{n} x^{i} = \frac{x^{n + 1} - 1}{x - 1}$
Das ist die Formel für die endliche geometrische Partialsumme.
4
Für welche ganzen Zahlen ist $2^{n} > n^{2}$ ? (Probieren ist hier besser als rechnen!)
5
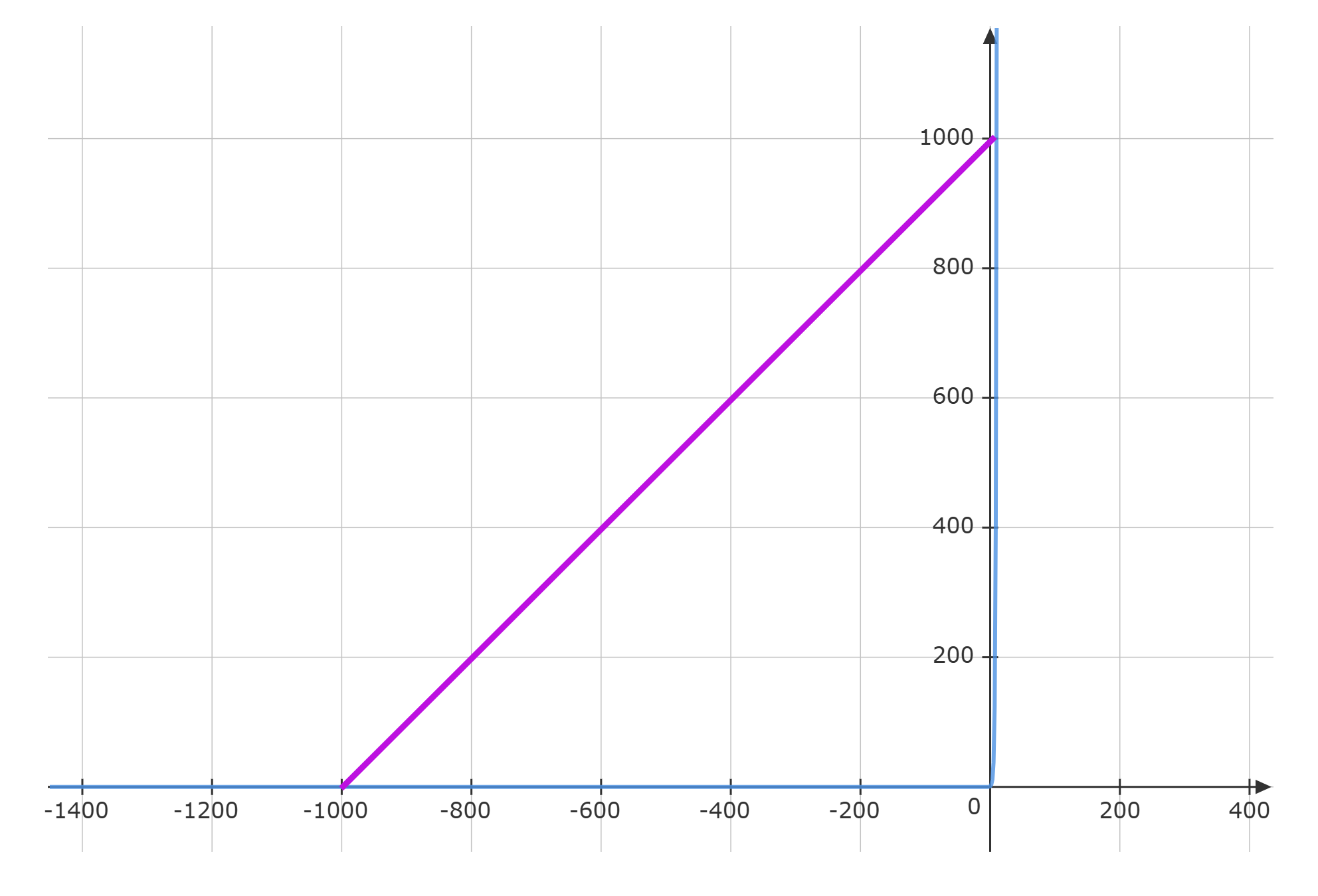
Gegeben ist die Funktion: $f (x) = 2^{x}$ für die ganzen Zahlen $- 1000, . . ., 10$
1. Diskutiere den Satz: "Der Graph der Exponentialfunktion ergibt einen rechten Winkel".
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  Zuerst lohnt es sich, den Graphen der Funktion $f (x)$ in ein passendes Koordinatensystem zu zeichnen:
  Dabei erkennt man, dass der Graph $G_{f}$ in seinem Verlauf dem negativen Teil der x-Achse und dem positiven Teil der y-Achse folgt.
  Berechnet man die gegebenen Endpunkte, ergeben sich folgende Werte:
  $2^{- 1000} \approx 0$
  $2^{10} = 1024$
  Die beiden Punkte liegen also ungefähr bei $(0 | 1000)$ und $(- 1000 | 0)$ und bilden mit dem Ursprung ein rechtwinkliges Dreieck, bei dem die beiden Katheten, an denen der Graph anliegt, einen rechten Winkel bilden.
  Man muss jedoch beachten, dass vor allem der Punkt $(0 | 1000)$ ziemlich stark gerundet ist. Der eigentliche Punkt auf dem Graphen liegt weiter oben und weiter rechts, weshalb der Winkel in Wirklichkeit um ein gutes halbes Grad größer als $90 °$ ist.
  Insgesamt kann man also sagen, dass der Graph der Funktion zwar einem rechten Winkel ähnelt, aber es eben doch kein perfekter $90 °$ -Winkel ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle eine Skizze der Funktion oder benutze einen Funktionsplotter
  Erkläre die Argumente, die für oder gegen die Behauptung sprechen
2. Bestimme die kleinste Zahl $x_{0}$ , so dass für alle $x \geq x_{0}$ gilt: $2^{x} \geq 16 x^{3}$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Logarithmus
  Um $x_{0}$ zu finden, setzt man $2^{x}$ und $16 x^{3}$ gleich und stellt nach $x$ um.
  $2^{x}$ $=$ $16 x^{3}$ $\log_{2}$
  $x$ $=$ $\log_{2} 16 x^{3}$
  ↓
  Logarithmus-Regel: Produkt zu Summe
  $x$ $=$ $\log_{2} 16 + \log_{2} x^{3}$
  ↓
  Logarithmus-Regel: Potenz zu Produkt
  $x$ $=$ $4 + 3 \cdot \log_{2} x$
  Jetzt muss man ausprobieren, bis man den richtigen Wert für $x$ gefunden hat.
  Da man bei $\log_{2} x$ nur positive Werte für $x$ nur positive Werte einsetzen kann, muss $x$ positiv sein. Außerdem muss $x$ eine Zweierpotenz sein.
  $x$
  $1$
  $2$
  $4$
  $8$
  $16$
  $4 + 3 \cdot \log_{2} x$
  $4$
  $7$
  $10$
  $13$
  $16$
  $x_{0}$ hat den Wert $16$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wie ändert sich die Antwort in b), wenn die rechte Seite ( $16 x^{3}$ ) mit $2^{13} = 8192$ multipliziert wird, also die Ungleichung $2^{x} \geq 131072 x^{3}$ betrachtet wird?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Logarithmus
  Hier geht man genau wie in Teilaufgabe b) vor, man ersetzt nur $16 x^{3}$ durch $131072 x^{3}$ .
  $2^{x}$ $=$ $131072 x^{3}$ $\log_{2}$
  $x$ $=$ $\log_{2} 131072 x^{3}$
  ↓
  Logarithmus-Regel: Produkt zu Summe
  $x$ $=$ $\log_{2} 131072 + \log_{2} x^{3}$
  ↓
  Logarithmus-Regel: Potenz zu Produkt
  $x$ $=$ $17 + 3 \cdot \log_{2} x$
  Jetzt muss man ausprobieren, bis man den richtigen Wert für $x$ gefunden hat.
  Da man bei $\log_{2} x$ nur positive Werte für $x$ nur positive Werte einsetzen kann, muss $x$ positiv sein. Außerdem muss $x$ eine Zweierpotenz sein.
  $x$
  $1$
  $2$
  $4$
  $8$
  $16$
  $32$
  $17 + 3 \cdot \log_{2} x$
  $17$
  $20$
  $23$
  $26$
  $29$
  $32$
  Hier hat $x_{0}$ den Wert $32$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
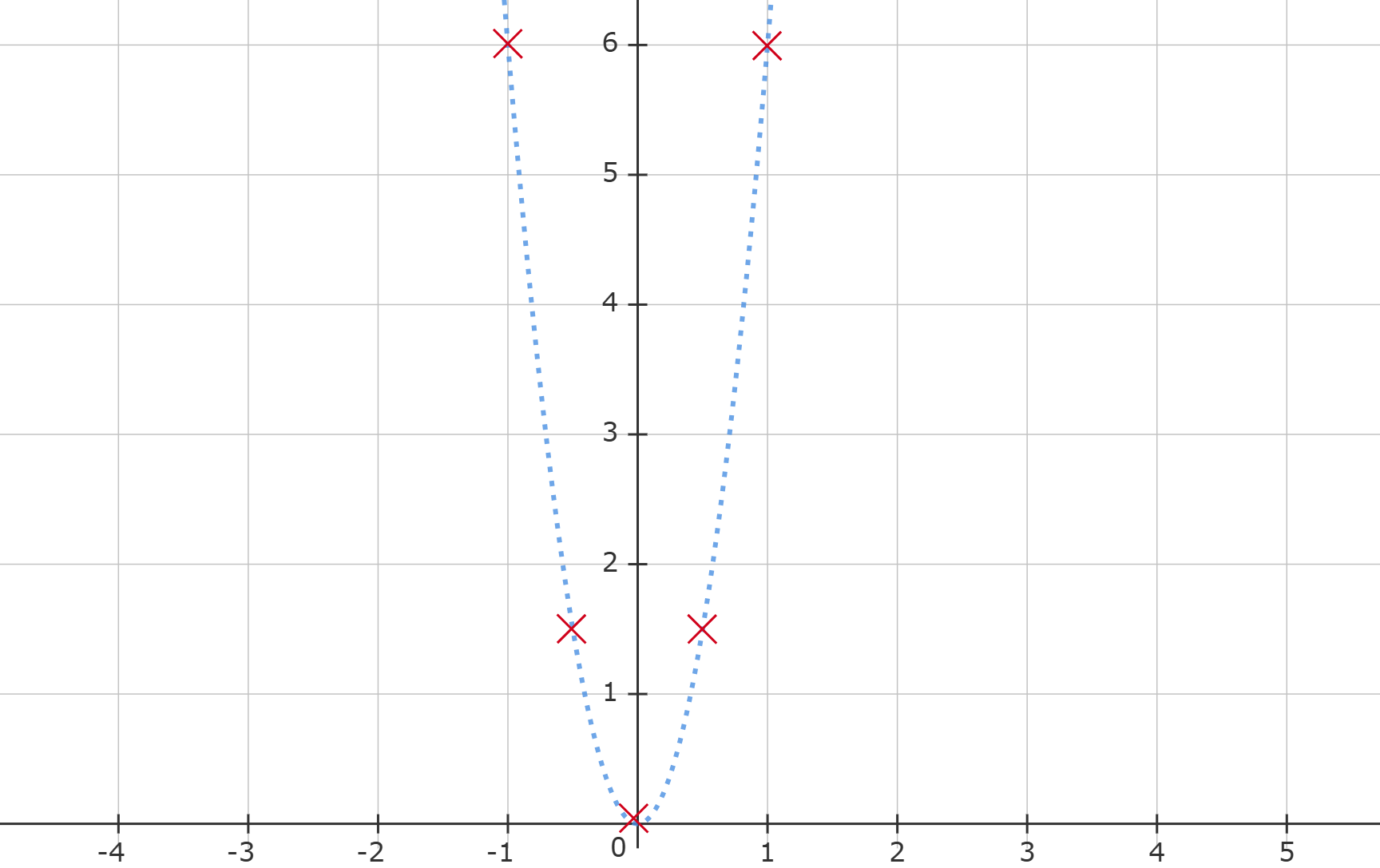
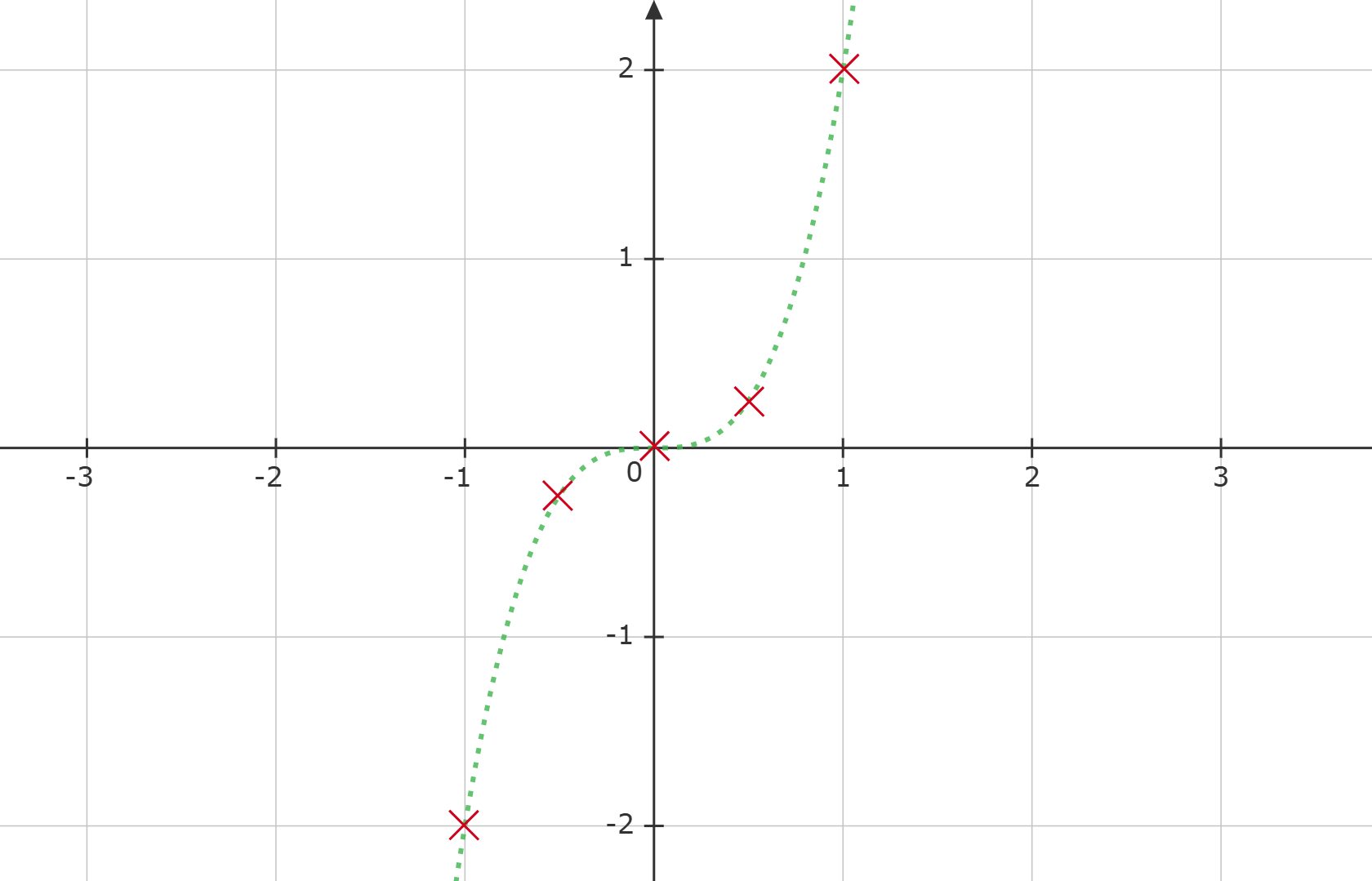
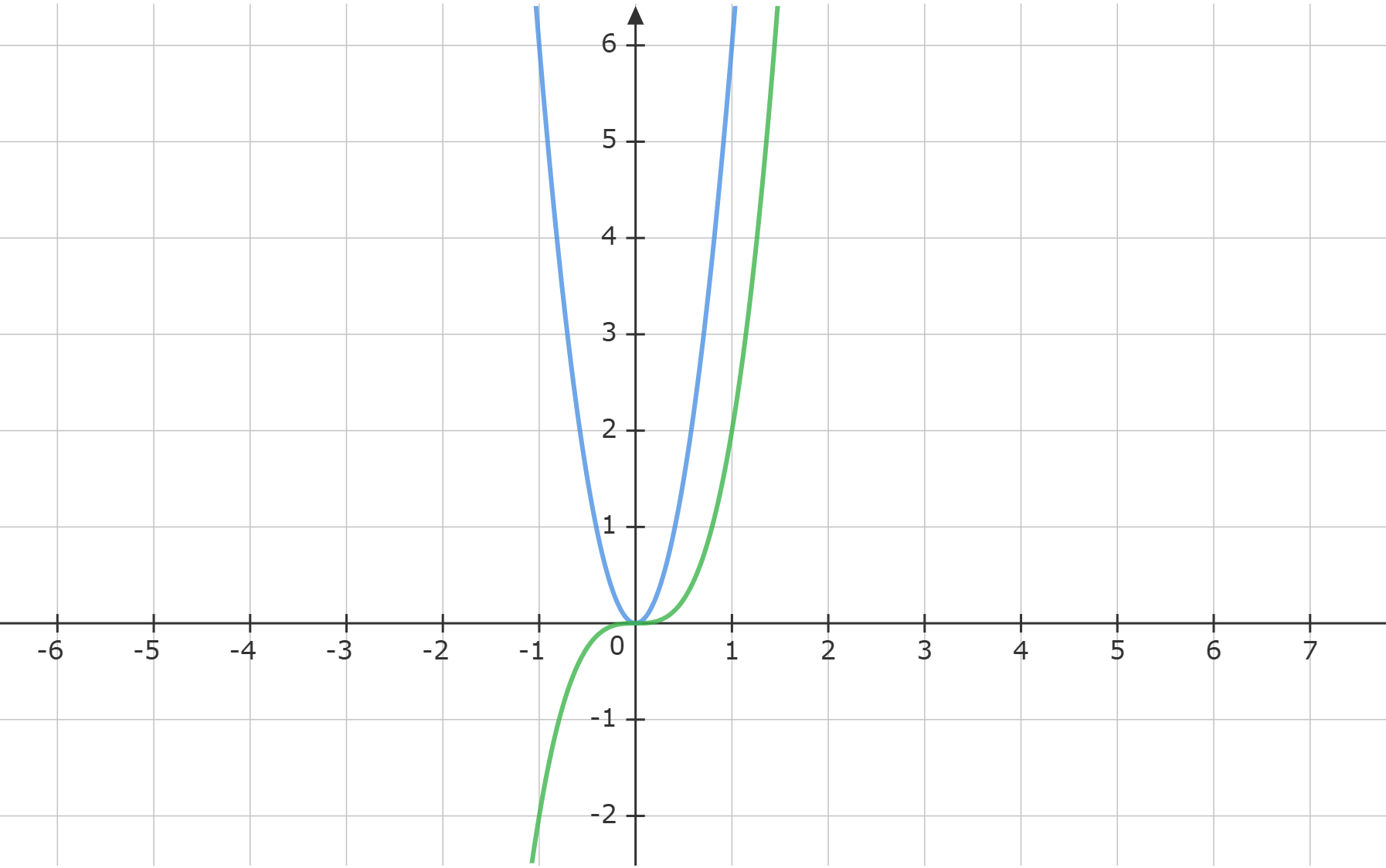
Gegeben sind die beiden Funktionen $f (x) = 6 \cdot x^{2}$ und $g (x) = 2 \cdot x^{3}$ .
1. Skizziere beide Graphen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Erstellen von Wertetabellen
  Zuerst setzt man ein paar Werte in die beiden Funktionen ein und schreibt sie in eine Tabelle:
  $f (x) = 6 \cdot x^{2}$ :
  x
  $- 1$
  $- 0,5$
  $0$
  $0,5$
  $1$
  f(x)
  $6$
  $1,5$
  $0$
  $1,5$
  $6$
  $g (x) = 2 \cdot x^{3}$ :
  x
  $- 1$
  $- 0,5$
  $0$
  $0,5$
  $1$
  f(x)
  $- 2$
  $- 0,25$
  $0$
  $0,25$
  $2$
  Eintragen der Werte in ein Koordinatensystem
  Man markiert die zuvor markierten Werte und verbindet sie:
  Fertigstellen der Skizze
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne einzelne Werte der Funktion
  Markiere sie in einem Koordinatensystem
  Verbinde die Punkte
2. Für welche x ist $f (x) = g (x)$ ? Für welche ist $f (x) > g (x)$ und für welche $f (x) < g (x)$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Funktionen gleichsetzen
  An den Graphen kann man schon einen Wert ablesen, bei dem die beiden Funktionen den gleichen Wert haben, nämlich bei $x = 0$ . Um weitere Werte zu bestimmen setzt man die Funktionen gleich:
  $f (x)$ $=$ $g (x)$
  $6 \cdot x^{2}$ $=$ $2 \cdot x^{3}$ $/ 6 \cdot x^{2}$
  $1$ $=$ $\frac{2 \cdot x^{3}}{6 \cdot x^{2}}$
  $1$ $=$ $\frac{1}{3} \cdot x$ $\cdot 3$
  $3$ $=$ $x$
  Bei den x-Werten $0$ und $3$ schneiden sich die Funktionen $f (x)$ und $g (x)$ .
  Ungleichung aufstellen
  Um herauszufinden, für welche $x$ -Werte die Werte von $f (x)$ größer (bzw. kleiner) als die von $g (x)$ sind, stellt man eine Ungleichung auf:
  $f (x)$ $>$ $g (x)$
  $6 \cdot x^{2}$ $>$ $2 \cdot x^{3}$ $/ 6 \cdot x^{2}$
  $1$ $>$ $\frac{2 \cdot x^{3}}{6 \cdot x^{2}}$
  $1$ $>$ $\frac{1}{3} \cdot x$ $\cdot 3$
  $3$ $>$ $x$
  Für $x < 3$ (außer bei $x = 0$ ) ist $f (x) > g (x)$ . Umgekehrt ist $f (x)$ für $x > 3$ kleiner als $g (x)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

$x$	$1$	$2$	$4$	$8$	$16$
$4 + 3 \cdot \log_{2} x$	$4$	$7$	$10$	$13$	$16$

$x$	$1$	$2$	$4$	$8$	$16$	$32$
$17 + 3 \cdot \log_{2} x$	$17$	$20$	$23$	$26$	$29$	$32$

x	$- 1$	$- 0,5$	$0$	$0,5$	$1$
f(x)	$6$	$1,5$	$0$	$1,5$	$6$

x	$- 1$	$- 0,5$	$0$	$0,5$	$1$
f(x)	$- 2$	$- 0,25$	$0$	$0,25$	$2$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$2^{x}$	$=$	$16 x^{3}$	$\log_{2}$
$x$	$=$	$\log_{2} 16 x^{3}$
	↓	Logarithmus-Regel: Produkt zu Summe
$x$	$=$	$\log_{2} 16 + \log_{2} x^{3}$
	↓	Logarithmus-Regel: Potenz zu Produkt
$x$	$=$	$4 + 3 \cdot \log_{2} x$

$2^{x}$	$=$	$131072 x^{3}$	$\log_{2}$
$x$	$=$	$\log_{2} 131072 x^{3}$
	↓	Logarithmus-Regel: Produkt zu Summe
$x$	$=$	$\log_{2} 131072 + \log_{2} x^{3}$
	↓	Logarithmus-Regel: Potenz zu Produkt
$x$	$=$	$17 + 3 \cdot \log_{2} x$

$f (x)$	$=$	$g (x)$
$6 \cdot x^{2}$	$=$	$2 \cdot x^{3}$	$/ 6 \cdot x^{2}$
$1$	$=$	$\frac{2 \cdot x^{3}}{6 \cdot x^{2}}$
$1$	$=$	$\frac{1}{3} \cdot x$	$\cdot 3$
$3$	$=$	$x$

Aufgaben zum Thema Potenzen und Polynome

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Erstellen von Wertetabellen

Eintragen der Werte in ein Koordinatensystem

Fertigstellen der Skizze

Hast du eine Frage oder Feedback?

Funktionen gleichsetzen

Ungleichung aufstellen

Hast du eine Frage oder Feedback?