Die Abbildung zeigt ein Dreiecksprisma, aus dem ein Halbzylinder ausgespart wurde.
Berechne das Volumen des Körpers.
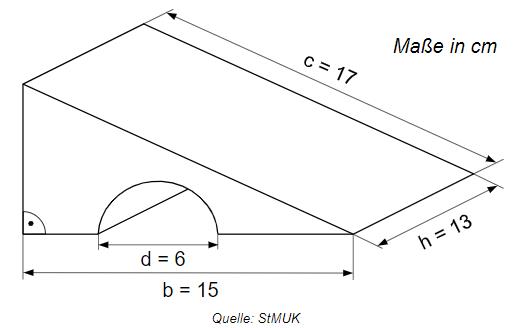
Hinweis: Skizze nicht maßstabsgetreu
cm³Die Kantenlänge wird verdoppelt. Erkläre, wie sich dadurch das Volumen verändert.
Die Abbildung zeigt ein Dreiecksprisma, aus dem ein Halbzylinder ausgespart wurde.
Berechne das Volumen des Körpers.

Hinweis: Skizze nicht maßstabsgetreu
Die Kantenlänge wird verdoppelt. Erkläre, wie sich dadurch das Volumen verändert.