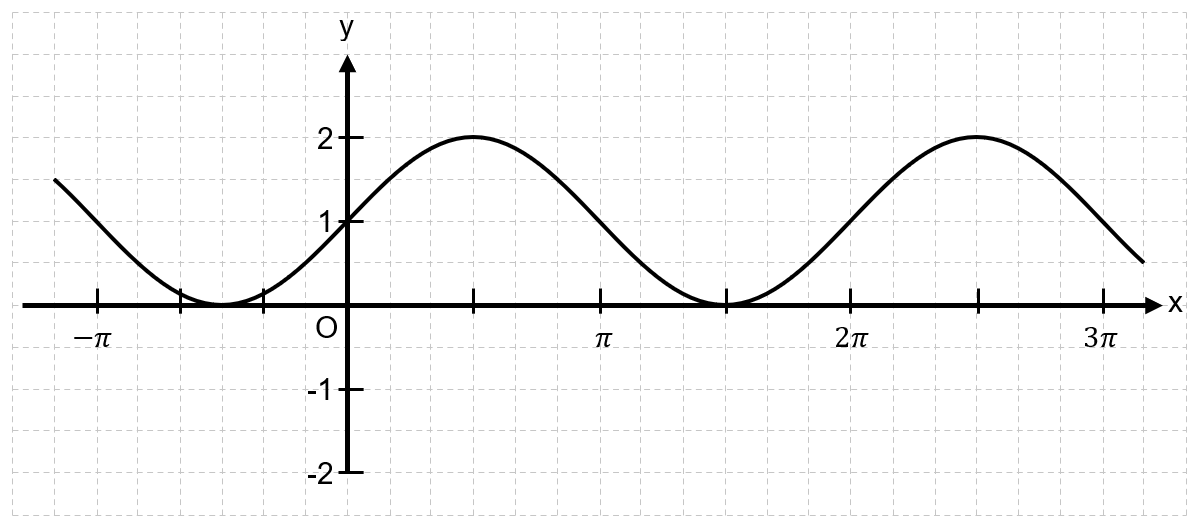
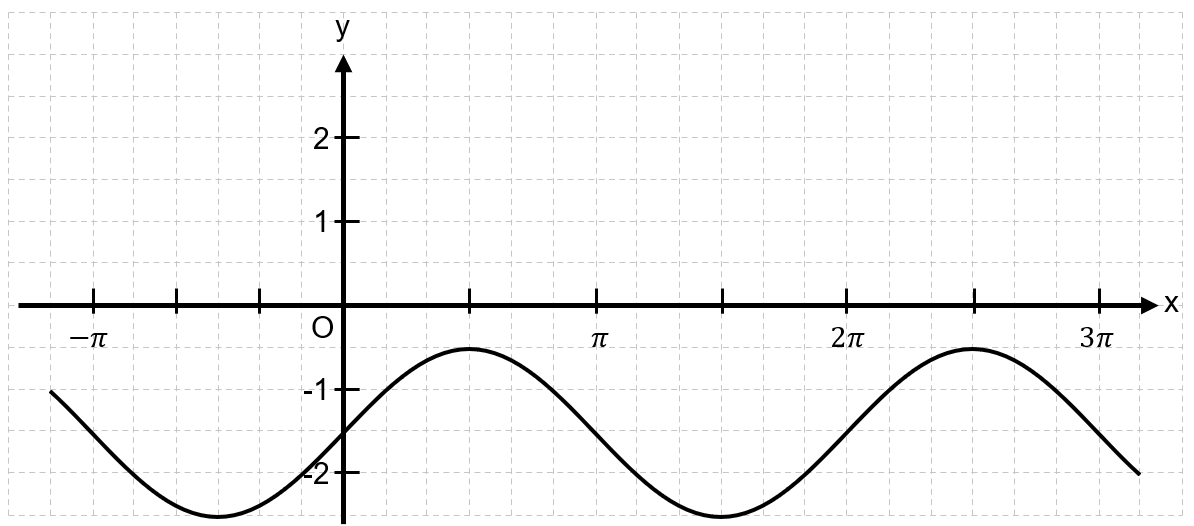
In den folgenden Diagrammen ist jeweils der Graph einer Funktion
mit gezeichnet.
Bestimme jeweils den Parameter
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
In den folgenden Diagrammen ist jeweils der Graph einer Funktion
mit gezeichnet.
Bestimme jeweils den Parameter