geg.: $\overrightarrow {OP_n}(\varphi)= \begin{pmatrix} 5\cdot \sin\varphi \\ 5\cdot \cos\varphi \end{pmatrix}$; $\overrightarrow {OQ_n}(\varphi)= \begin{pmatrix} -2\cdot \mathbf{\sin^2\varphi} \\ \dfrac{4}{\sin\varphi} \end{pmatrix}$; $\varphi=80°$

ges.: Koordinaten $\overrightarrow {OP_1}$ und $\overrightarrow {OQ_1}$ für $\varphi=80°$; Zeichnung Dreieck $OP_1Q_1$

Berechnung der Koordinaten für $\overrightarrow {OP_1}(\varphi=80°)$:

$\overrightarrow {OP_1}(\varphi=80°)= \begin{pmatrix} 5\cdot {\sin80°} \\ 5\cdot {\cos 80°} \end{pmatrix}=\begin{pmatrix} 5\cdot {0{,}98481} \\ 5\cdot {0{,}17365} \end{pmatrix}=\mathbf{\begin{pmatrix} 4{,}92 \\ 0{,}87 \end{pmatrix}}$

Berechnung der Koordinaten für $\overrightarrow {OQ_1}(\varphi=80°)$

$\Rightarrow \overrightarrow {OQ_1}(\varphi=80°)= \begin{pmatrix} -2\cdot \sin^2(80°) \\ \dfrac{4}{\sin 80°} \end{pmatrix}$

$\hphantom{\Rightarrow}=\begin{pmatrix} {-2\cdot 0{,}98481^2} \\ \dfrac{4}{0{,}98481} \end{pmatrix}=\mathbf {\begin{pmatrix} {-1{,}94} \\ 4{,}06 \end{pmatrix}}$

Einzeichnen des Dreiecks $OP_1Q_1$ in das KOSY

geg.: Behauptung : Strecke $[OP_n]=const.$

ges.: Begründung durch rechnerischen Nachweis

Berechnung der Strecken aus den Koordinaten

Mit dem Satz des Pythagoras gilt:

$\overrightarrow {OP_n}(\varphi)= \begin{pmatrix} 5\cdot \sin\varphi \\ 5\cdot \cos\varphi \end{pmatrix}\\$$\mathbf{\overline{OP_n}(φ)^2=(5\cdot sin\varphi)^2+(5\cdot cos\varphi)^2}$

${\overline{OP_n}^2(φ)={25\cdot (\sin\varphi)^2+25\cdot (\cos\varphi)^2}}$

$\hphantom{{\overline{OP_n}^2(φ)}}=25 \cdot(\sin^2 \varphi+\cos^2 \varphi)$

$\hphantom{{\overline{OP_n}^2(φ)}}=25$ (trigonometrischer Pythagoras)

Daher ist:

$\mathbf{ \overline{OP_n}(φ)=\sqrt{25}\ LE =5\ LE}$ für alle $\varphi \in]0°;90°]\qquad$q.e.d.

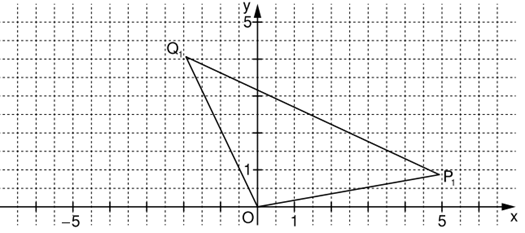
geg.: Vektoren $\overline{OP_1}(80°)=\begin{pmatrix} 4{,}92 \\ 0{,}87 \end{pmatrix}$ und $\overline{OQ_1}(80°)=\begin{pmatrix} -1{,}94 \\ 4{,}06 \end{pmatrix}$ gem. Aufgabe 3a

ges.: $∡ P_1OQ_1$

Berechnung mit Kosinussatz aufgelöst nach Kosinus $γ$

$c^2=a^2+b^2-2ab\cdot \cos(γ)\qquad\qquad$|$-c^2$

$0=c^2+a^2+b^2-2ab\cdot \cos(γ)\qquad\:\:$|$+ 2ab\cdot \cos(γ)$

$2ab\cdot \cos(γ)=-c^2+a^2+b^2\qquad\quad$ | $: 2ab$

$\displaystyle\cos(γ)=\frac{-c^2+a^2+b^2}{2ab}$

Berechnung von $a, b, c$ und $cos(γ)$

$\Rightarrow a: ≙ |\overline {OP_1}|=5\:\qquad$für alle $\varphi$ nach Teil b)

$\Rightarrow b: ≙ |\overline {OQ_1}|=\sqrt{-1{,}94^2+4{,}06^2}=\sqrt{3{,}76+16{,}48}=\sqrt{20{,}24}=4{,}50$

Berechnung Vektor $\overrightarrow {P_1Q_1}$ mit Vektoraddition $\overrightarrow{OP_1}\oplus\overrightarrow{P_1Q_1}=\overrightarrow {OQ_1}$

umgestellt nach $\overrightarrow{P_1Q_1}=\overrightarrow {OQ_1}-\overrightarrow{OP_1}=\begin{pmatrix} -1{,}94 \\ 4{,}06 \end{pmatrix}-\begin{pmatrix} 4{,}92 \\ 0{,}87 \end{pmatrix}=\begin{pmatrix} -6{,}86 \\ 3{,}19 \end{pmatrix}$

$c^2= \mathbf{\overrightarrow{|P_1Q_1|^2}}={(-6{,}86)^2+3{,}22^2}={47{,}06+10{,}18}={57{,}24}$

Die Werte von $a^2$ und $b^2$ sind schon oben berechnet worden.

$\displaystyle\Rightarrow \mathbf{\cos(∡P_1 OQ_1 )}=\frac{-c^2+a^2+b^2}{2ab}$

$\displaystyle=\frac{-57{,}46+25+20{,}24}{2\cdot5\cdot4{,}50} =\frac{-12{,}22}{45}=\mathbf{-0{,}27}$

Falls $\cos(∡P_1OQ_1 )$ negativ, so ist $∡P_1OQ_1$ zwischen $90°$ und $180°$ groß.

Kosinuswert $\mathbf{∡P_1OQ_1=-0{,}27 \qquad \Rightarrow ∡P_1 OQ_1=105{,}76^\circ}$