Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Aufgabe A1
Mia lernt in der Schule den Begriff „Inflation“ kennen. Damit wird der Preisanstieg von Produkten über einen bestimmten Zeitraum hinweg bezeichnet. Dieser Zusammenhang lässt sich unter der Annahme einer gleichbleibenden jährlichen Preissteigerung von näherungsweise durch eine Funktion mit einer Gleichung der Form
beschreiben. Dabei steht für den Anfangspreis eines Produkts und für dessen Preis nach Jahren. Mia kauft ihrer Mutter jährlich am 1. Juni Rosen beim örtlichen Blumenladen.
Am 1. Juni 2020 kostete eine Rose noch . Am 1. Juni 2022 lag der Preis pro Rose bei .
Berechnen Sie den voraussichtlichen Preis einer Rose am 1. Juni 2027 unter der Voraussetzung, dass die jährliche Preissteigerung von gleich bleibt. (3 P)
Runden Sie auf zwei Stellen nach dem Komma.
[Zwischenergebnis: ]
Berechnen Sie, in welchem Jahr Mia erstmals mehr als doppelt so viel für eine Rose bezahlen müsste wie am 1. Juni 2020, wenn man von einer jährlichen Preissteigerung von ausgeht. (2 P)
- 2
Aufgabe A2
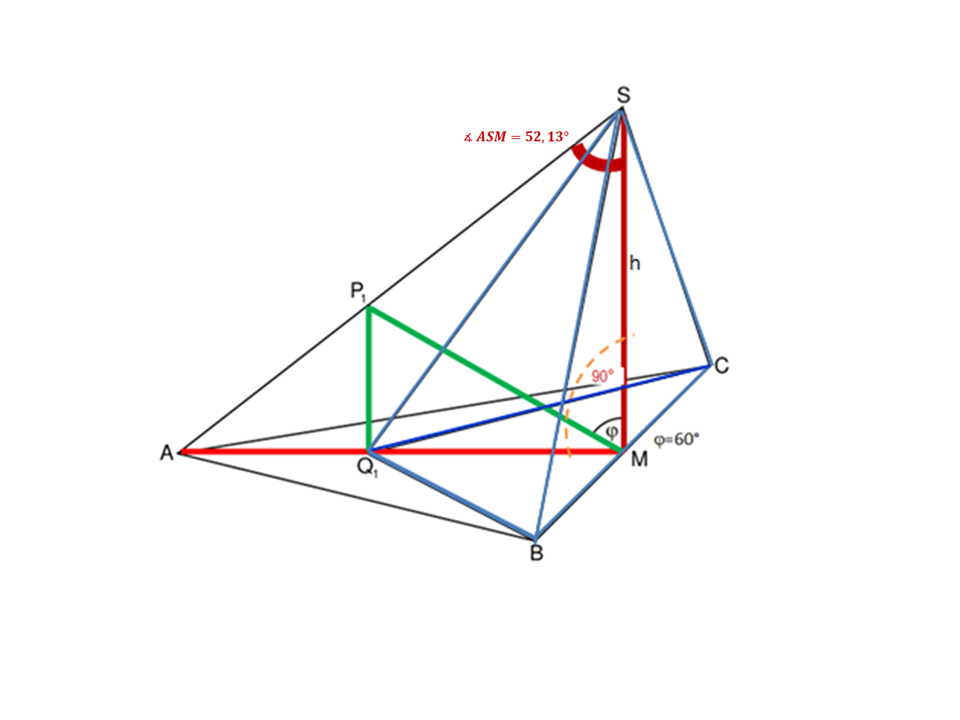
Die Strecke mit dem Mittelpunkt ist die Basis des gleichschenkligen Dreiecks . Dieses Dreieck ist die Grundfläche der Pyramide mit der Höhe .
Es gilt: ; ; .
Die Zeichnung zeigt ein Schrägbild der Pyramide . In der Zeichnung gilt: ; .
liegt auf der Schrägbildachse.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
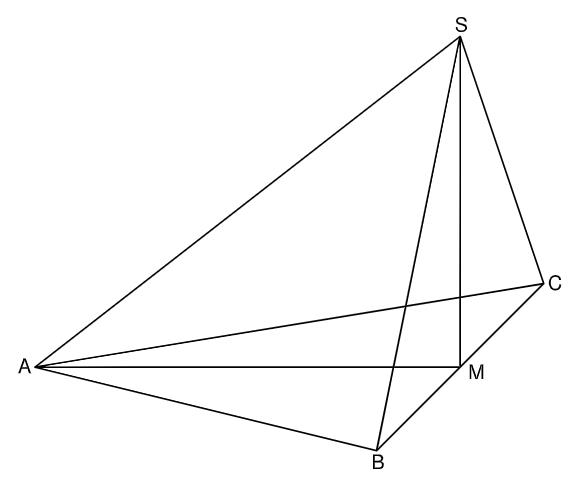
Berechnen Sie das Maß des Winkels . (1 P)
Ergebnis:
Punkte liegen auf der Strecke . Die Winkel haben das Maß mit
. Punkte liegen auf der Strecke mit . Die Dreiecke sind die Grundflächen der Pyramiden mit der Spitze und der Höhe .
Zeichnen Sie die Strecken [] und [] sowie die Pyramide für in das Schrägbild zur Aufgabenstellung ein. (2 P)
Zeigen Sie rechnerisch, dass für die Länge der Strecken in Abhängigkeit von gilt:
Die Länge der Strecke ist minimal. Geben Sie den zugehörigen Wert für an. (3 P)
°Zeigen Sie rechnerisch, dass für die Länge der Strecken in Abhängigkeit von gilt: (3 P)
Berechnen Sie sodann das Volumen der Pyramide
- 3
Aufgabe A3
Pfeile und mit spannen für
Dreiecke auf.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
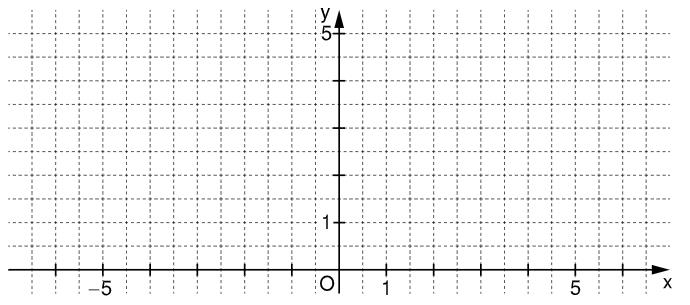
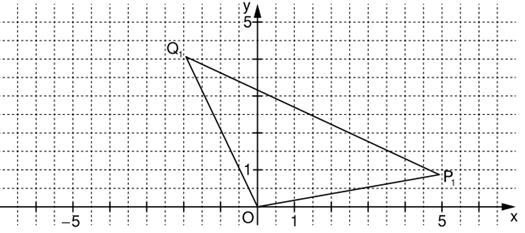
Geben Sie für die Koordinaten der Pfeile und an.
Zeichnen Sie sodann das Dreieck in das Koordinatensystem zur Aufgabenstellung ein. (2 P)
Begründen Sie rechnerisch, weshalb die Länge der Strecken konstant ist. (2 P)
Berechnen Sie das Maß des Winkels (2 P)
°
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?