Stellen mit waagerechten Tangenten ermitteln

Da sich bei ganzrationalen Funktionen das Monotonieverhalten nur an Stellen mit waagerechten Tangenten (Steigung m=0) ändern kann, suchst du die Nullstellen der Ableitung.

$f(x)=x^4-\frac{4}{3}{x}^3-12x^2+3f(x)=x^4-\backslash frac\; 4\; 3x^3-12x^2+3$

Bilde die Ableitung:

$f^{\mathrm{\prime }}(x)=4x^3-4x^2-24xf\text{'}(x)=4x^3-4x^2-24x$

Setzte die Ableitung mit 0 gleich und löse die Gleichung:

Aufgrund des Satzes vom Nullprodukt kannst du die Faktoren getrennt betrachten, um die Nullstellen zu bestimmen.

Die erste Nullstelle ist direkt $x_1=0x\_1=0$. Die zweite erhältst du mithilfe der Mitternachtsformel aus

$x^2-x-6=0x^2-x-6=0$

Mitternachtsformel: $x_{\mathrm{2,3}}={\displaystyle \frac{1\pm \sqrt{(-1{)}^2-4\cdot 1\cdot (-6)}}{2\cdot 1}}x\_\{2\{,\}3\}=\backslash dfrac\{1\backslash pm\backslash sqrt\{(-1)^2-4\backslash cdot\; 1\; \backslash cdot\; (-6)\}\}\{2\backslash cdot\; 1\}$ liefert $x_2=3x\_2=\; 3$ und $x_3=-2x\_3=-2$.

Lösung mithilfe einer Skizze des Graphen der Ableitung

Es handelt sich lediglich um eine Skizze, deshalb brauchst du nur:

• Die Nullstellen von f' und ihre Vielfachheit (alle Nullstellen sind hier mit Vielfachheit 1)

• Den Grad und Leitkoeffizienten von f' für den Globalverlauf.

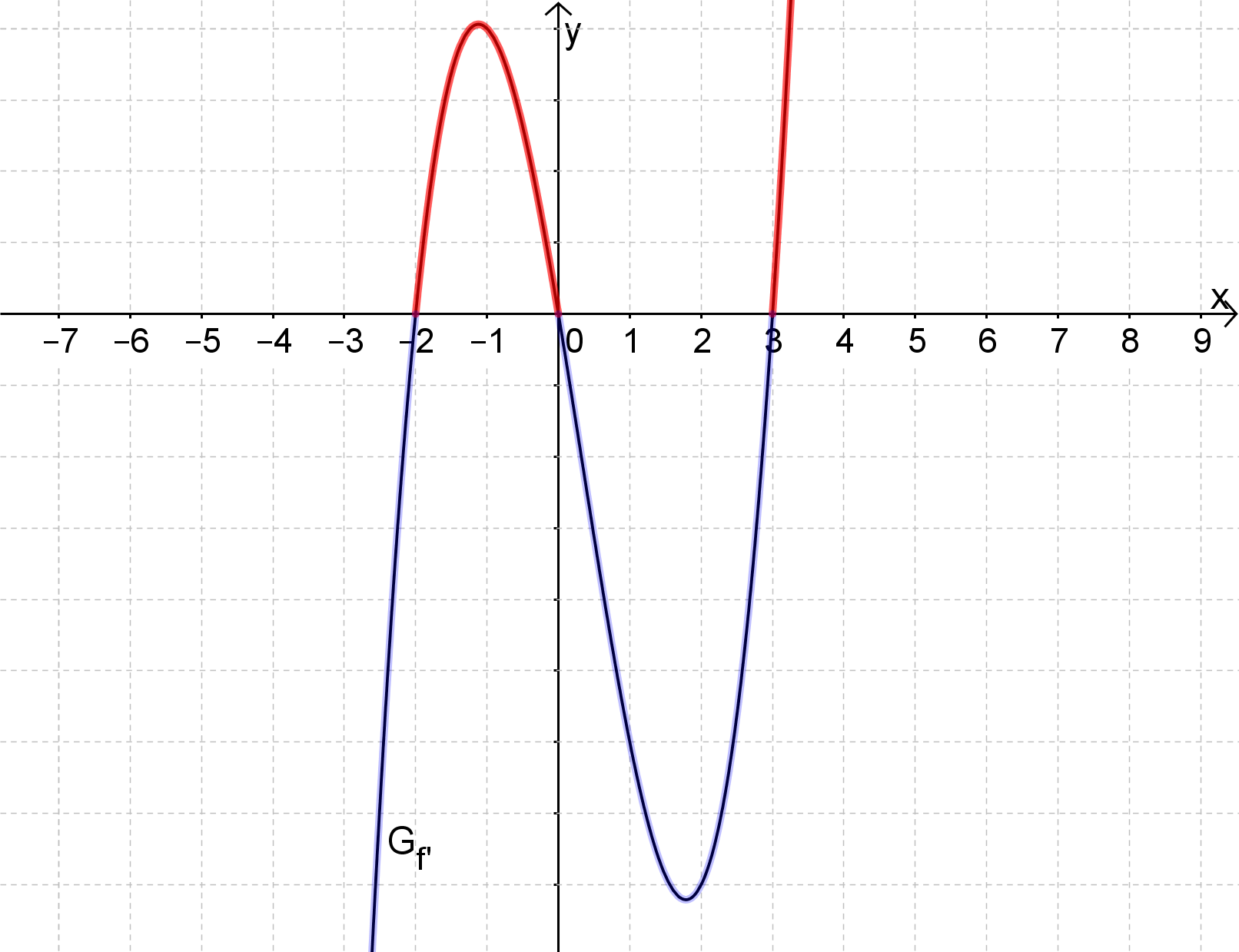
• Trage zunächst die Nullstellen an. Es sind alles einfache, also schneidende Nullstellen.

• Der Grad ist ungerade (3) und der Leitkoeffizent positiv, der Graph kommt also von unten.

• Jetzt musst du nur noch entsprechend der Vielfachheiten die x-Achse schneiden.

Der Graph der Ableitungsfunktion zeigt für jeden x-Wert die Steigung, die der zugehörige Punkt von $G_{f}G\_f$ an dieser Stelle hat. Steigt der Graph in einem Bereich, so ist der Wert der Steigung positiv und $G_{f^{\mathrm{\prime }}}G\_\{f\text{'}\}$ verläuft oberhalb der x-Achse. Umgekehrt verläuft $G_{f^{\mathrm{\prime }}}G\_\{f\text{'}\}$ unterhalb der x-Achse, wenn $G_{f}G\_f$ fällt.

Der Graph $G_{f}G\_f$ ist also streng monoton steigend für $x\in [-2;0]\cup [3;+\mathrm{\infty }[x\backslash in[-2;0]\backslash cup[3;+\backslash infty[$ und streng monoton fallend für $x\in ]-\mathrm{\infty };-2]\cup [0;3]x\backslash in]-\backslash infty;-2]\backslash cup[0;3]$.

(Nicht gefragt: Bei $x=-2x=-2$ und $x=3x=3$ liegen Tiefpunkte, bei $x=0x=0$ ein Hochpunkt)

Alternative Lösung über Monotonietabelle

Wenn du nicht zeichnen möchtest, kannst du das gleiche schriftlich mit einer Monotonietabelle machen.

• Die Spalten beschreiben die Nullstellen der Ableitungsfunktion und die Bereiche zwischen diesen

• Die mittlere Zeile zeigt das Vorzeichen von f' in diesem Bereich an

• Die unterste Zeile enthält direkt das Monotonieverhalten

Auf die Inhalte der 2. Zeile kommst du entweder durch ähnliche Überlegungen wie schon bei der Skizze oder du setzt - im Kopf oder im Taschenrechner - einen Beispielwert aus diesem Bereich ein.

Die Inhalte der 3. Zeile folgen aus denen der 2. Zeile, wobei du zuerst die Pfeile einzeichnest und dann die Angabe zu Hochpunkt, Tiefpunkt oder Terrasenpunkt ergänzt.