1 Wozu dient diesen Kurs?
Abb.: Viele stellen sich diese Frage. Was genau ist was?
Sicherlich hast Du all diese Begriffe schon einmal gehört, nur Hand aufs Herz, kennst Du genau die Unterschiede und könntest Du diese jemanden erklären?
In diesem Kurs fügen wir die Begriffe Schritt für Schritt für Dich zusammen, was Du bislang schon gelesen, erarbeitet oder möglicherweise nicht in direktem Zusammenhang gesehen hast. Viel Spaß dabei, los gehts!
2 Elektrisches Feld

Anm.: Verursacht durch jede Ladung
Zur Wiederholung und Einstimmung kannst Du Dir gerne ergänzende Artikel ansehen:
LINK: Elektrisches Feld, Teil 1 und Elektrisches Feld, Teil 2
Wir beginnen unseren Kurs mit einem Elektrischen Feld. Wer hätte das gedacht ;-)
Der Vollständigheit halber sei erwähnt, dass es natürlich auch magnetische Felder und Gravitationsfelder gibt, welche aber in diesem Kurs nicht behandelt werden.
Konkret eignet sich für unsere weiteren Betrachtungen am besten ein homogenes elektrisches Feld um die Besonderheit einer konstanten elektrischen Feldstärke E (Vektorschreibweise: ) ausnützen zu können, ansonsten wären alle weiteren Ableitungen zu komplex und würden Dich vom Wesentlichen ablenken. Soweit so gut.
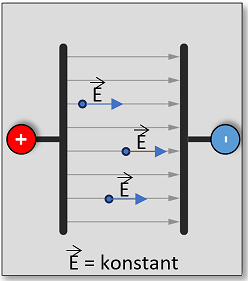
Abb.: Homogenes elektrisches Feld eines Plattenkondensators
Jede Ladung (sei es eine Punktladung q entsprechend einer Elematarladung e bzw. Vielfache Q davon) umgibt immer ein Elektrisches Feld
Ein Elektrisches Feld wiederum bedingt immer eine Elektrische Feldstärke E. Das eine existiert nicht ohne das andere. E drückt die Wirkung des Elektrischen Feldes aus
3 Elektrische Feldstärke (E)

Anm.: Die Wirkung jeden elektrischen Feldes
Die Feldstärke E drückt die Wirkung des Elektrischen Feldes aus. Ansonsten würde wir die Existenz eines Elektrischen Feldes überhaupt nicht bemerken.
Die Wirkung ist konkret eine elektrische Kraft auf beispielsweise eine Probeladung q, welche eine Elementarladung +e oder -e darstellen kann. Die Probeladung benötigen wir um überhaupt eine Wirkung im Elektrischen Feld provozieren zu können.
Wir können diese Kraft ausdrücken und berechnen mit einer uns schon bekannten Formel:
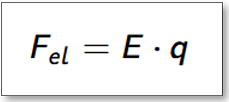
Die Kraft ist demnach umso größer...
... je größer die elektrische Feldstärke E
... oder/und je größer die Ladung q (bzw. jede x-beliebige Ladung Q) ist
Verwechsle diese Kraft, hervorgerufen durch die Elektrische Feldstärke E, nicht mit der Coulombschen Kraft. Mit dem Coulombschen Gesetz berechnen wir die herrschende Kraft zwischen zwei Ladungen. LINK zum Thema
![Anm.: Wir haben die Formel etwas umgestellt; [E] =](https://assets.serlo.org/24eb5f80-3c66-11ee-b109-a3f2e53ad6dd/elektrischesfeldbiselektrischespannungeinspannungsbogen.png)
Anm.: Wir haben die Formel etwas umgestellt; [E] =
Die Elektrische Feldstärke () drückt die Elektrische Kraft () pro Ladungseinheit () aus. Wir brauchen diesen interessanten Zusammenhang für das weitere Verständnis.
Mit dem Übergang auf die nachfolgende Kursseite müssen wir uns bewußt machen, dass das Elektrische Feld (neben seiner Besonderheit eine Kraftwirkung auf Ladungen q oder Q auszuüben) noch mit einer weiteren Besonderheit aufwarten kann.

Anm.: Wir suchen eine weitere Besonderheit
4 Elektrisches Potential (Φ)

Anm.: Voila..., die weitere Besonderheit des elektrischen Feldes
Um unsere neue Besonderheit verständlich darstellen zu können, benutzen wir die Darstellung unseres bisherigen homogenen Elektrischen Feldes eines Plattenkondensators und ergänzen hierin eine Probeladunge q+, welche wir an den Orten A und B betrachten werden.
Ort A ist nahe der linken positiven Platte des Kondensators
Ort B ist nahe der rechten negativen Platte des Kondensators
Die Probeladung q+ ist klein genug ggü. der Ladungen Q+ und Q- der beiden Platten, sodass wir keine (nennenswerte) Beeiflussung des homogenen elektrischen Feldes erkennen und weiter als konstant angenommen werden kann
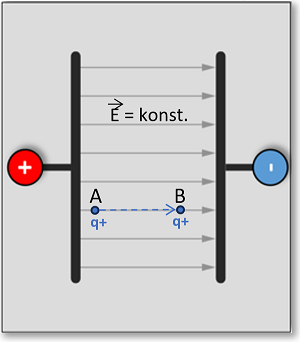
Abb.: Geänderte Versuchsanordnung nun mit einer (von A nach B) zu verschiebenenden Probeladung q+
Wir postulieren zunächst: Ein Elektrisches Potential (Φ für phi)
drückt die Potentielle Elektrische Energie () pro Ladungseinheit () aus
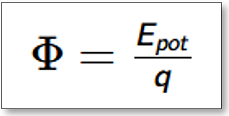
Einheiten: = J (für Joule); = C (für Coulomb);
(Zum Vergleich drückt die Elektrische Feldstärke ()
die Elektrische Kraft () pro Ladungseinheit () aus; Wir hatten hier als Einheit!)
Wie ist die "Einheit der Potentiellen Elektrischen Energie" also [] zu verstehen?
Um das "Vermögen" eines Elektrischen Potentials Φ zu verstehen, müssen wir alle beteiligten Größen und Einheiten verstehen. Die Ladungseinheit q in Coulomb ist bekannt. Wie verhält es sich allerdings mit der "Einheit zu " also ?
Dies ist neu an dieser Stelle also aufgepasst!
Die Einheit J (für Joule) ist eine Größe welche in der Physik auch für Arbeit verwendet wird. Anders ausgedrückt: Die physikalische Einheit der Arbeit (für "work" im Englischen) ist gleich der Einheit der Energie, nämlich das Joule: [E] = [A] = [W] = 1 J
Mit anderen Worten drückt ein Arbeitsvermögen gleich einer (gespeicherten) Energie aus
Überleitung zur nachfolgenden Kursseite
Interessant ist nun allerdings die Tatsache, dass an unseren zwei Orten A und B im homogenen elektrischen Feld unterschiedliche Potentielle Elektrische Energien () herrschen.
Warum dies so ist, erfahren wir auf der nächsten Kursseite.
Wenn allerdings (zunächst angenommen) an den Orten A und B gilt:
gilt ebenso die Ungleichheit für die Elektrischen Potentiale Φ an den Orten A und B
also (da die Ladungen q+ in unserem Fall identisch sind)
5 Elektrische Potentialdifferenz (ΔΦ)

Mit der Definition des Elektrischen Potentials () haben wir erkannt, das selbst im homogenen elektrischen Feld, Potentielle Elektrische Energien () je nach Ort der Betrachtung immer unterschiedliche Größe haben, damit auch Elektrische Potentiale ()
In unserem Falle hätten demnach die Messgrößen an den Orten A und B unterschiedliche Werte. Sind die Werte allerdings verschieden, ergibt sich immer eine Differenz, nachdem dies elektrische Potentiale betrifft, nennen wir diese auch Elektrische Potentialdifferenz ΔΦ
oder , da jeweils ist
Das Elektrische Potential am Ort B () ist kleiner gegenüber dem Elektrischen Potential am Ort A ().
Wichtig ist unbedingt anzumerken, das eine Elektrische Potentialdifferenz immer und ausschließlich zwischen zwei Orten/Punkten gemessen werden kann!
Warum entsteht an zwei verschieden Orten im elektrischen Feld überhaupt eine Potentialdifferenz ?
Wir beginnen im Plattenkondensator am Ort A. Dort sehr nahe an der positiven Platte des Kondensators mit der Ladung Q+ habe sich die Punktladung q+ abgelöst. An diesem Ort A habe die Punktladung q+ nun eine gewisse Potentielle Elektrische Energie ()
Im Plattenkondensator wirkt zwischen den Platten (von + nach - gerichtet) ein homogenes elektrischen Feld. Immer einhergehend mit entsprechender Feldstärke E. Jenes Feld bewirkt nun an der abgelösten Punktladung (noch an Ort A befindlich) eine Kraft gemäß der Formel
ist genau genommen als Vektor definiert, er hat also eine Größe und eine Richtung. Demnach wird die Kraft zu ebenso eine Richtung erhalten und zwar genau in Richtung der negativen Platte, eben auch jener Richtung des Elektrischen Feldes
Wirkt nun eine Kraft an der Ladung q+, erhält diese eine positive Beschleunigung, was aufgrund des Energieerhaltungssatzes bedeutet, dass von der bisherigen Potentiellen Elektrischen Energie () ein Teil in kinetische Energie umgewandelt werden muss, sich entsprechend reduziert, dies umsomehr, je mehr und weiter sich die Ladung q+ in Richtung der negativen Platte mit Ladung Q- bewegt.
Wir können hieraus also ableiten, dass alle rechts (in Richtung negativer Platte) eine niedrigere Energie besitzen. Nennen wir sie und platzieren diese inkl. der Ladung q+ am Ort B (siehe obige Skizze)
Bildet man nun eine Differenz im Sinne von erhält man ein negatives Resultat. Diese negative Differnz entspricht jener kinetischen Energie = Arbeit, welche für Beschleunigung des Bewegungsvorganges, kurz den Weg von A nach B, umgewandelt wurde.
Aufgrund des Formelzusammenhanges gilt nun ebenso , die Ladung q+ bleibt unverändert
Und schon haben wir die vorher postulierte Elektrische Potentialdifferenz
Herzlichen Glückwunsch!
;
[W] für Work in J; [q] für Coulomb = C
Die Elektrische Potentialdifferenz () entspricht jener Kinetischen Energie () pro Ladungseinheit (q), um welche sich die Elektrische Potentielle Energie vom Ort A hin zum Ort B () pro Ladungseinheit (q) verringert.

Puh! Geschafft!
6 Elektrische Spannung (U)

In den beiden vorangegangenen Kursseiten haben wir zwei Orte A und B betrachtet. Diese Betrachtungsweise führen wir für die Elektrische Spannung weiter, da sie nur zwischen zwei Punkten definiert und messbar ist.
Zwei Punkte können ...
... wie dargestellt innerhalb unseres gezeigten Plattenkondensators liegen
... Deine Hand und der Heizkörper Deiner Wohnung darstellen (Letzterer ist i.d.R. geerdet, man sagt auch er hätte ein Potential/Spannung = 0)
... zwei Drähte an einer Steckdose im Haus
... zwei Pole einer Batterie
... u.v.m. sein
Begriffsableitung der Elektrischen Spannung
Zu der in der vorigen Kursseite abgeleiteten Elektrischen Potentialdifferenz ergibt sich ausgehend von ...
... Elektrische Potentialdifferenz (wir ersetzen Potential durch Spannung)
... der Betriff Elektrische Spannungdifferenz oder kurz Elektrische Spannung
Die Elektrische Spannungsdifferenz deutet vom Namen schon auf die Differenz und den Bezug zwischen zwei Punkten hin, Elektrische Spannung ist inhaltlich gleichbedeutend, da ohnehin jeder diesen Umstand kennt. Nun du ebenso :-)
Einheit (für Volt)
Die internationale Einheit V (Volt) entspricht der elektrischen Spannung (U).
Diese wurde 1897 nach dem italienischen Physiker Alessandro Volta benannt
Beispiele vorkommender Spannungswerte in V (für Volt)
Bezeichnung | Elektrische Spannung (k für Kilo = 1.000) |
|---|---|
Batterien für Kleingeräte (z.B. Taschenlampen) | 1,5 V |
Autobatterien (Standard) | 12 V |
Haushaltsstrom (Steckdose) Drehstrom (Kraftsteckdose) | 230 V 380 V |
Oberleitung einer Bahntrasse | 15.000 V (15 kV) |
Hochspannungsleitungen | ab 110.000V (ab 110 kV ) |
Gewitterwolken gegen Erde | bis zu 100.000.000 V ( |
Weiterführende Informationen
Es sei an dieser Stelle angemerkt, dass die Gefährlichkeit und Wirkung auf den Menschen nicht nur von der Höhe der Spannung U abhängt! Weitere Informationen hierzu findest Du hier: LINK
Ergänzende Informationen zum Thema der Elektrischen Spannung findest Du ebenso hier: LINK
7 Zusammenfassung
Wir hatten uns in diesem Kurs viel vorgenommen. Ggf. scheinbar voneinander losgelöste Begriffe galt es zu erklären und in einen Zusammenhang zu setzen. Wir haben folgendes zusammengefasst erkannt:
In einem Elektrischen Feld (Kursseite 2) mit seiner Feldstärke (Kursseite 3) wirkt auf eine Probeladung q eine Kraft . Soweit so gut. Am Ort der Probeladung herrscht allerdings ebenso ein Elektrisches Potential (Kursseite 4), welche eine Potentielle Energie je Ladungseinheit darstellt. An einem differenten Ort herrscht eine andere potentielle Energie je Ladungseinheit. Zwischen diesen Orten/Punkten herrscht eine Potentialdifferenz (Kursseite 5), welche als Spannungsdifferenz (Kursseite 6) oder kurz Spannung definiert wird.
Wie fühlst du Dich? Ich hoffe Du konntest in diesem Themenkomplex den berühmten Roten Faden für Dich entdecken ...

