Teil B - lernen mit Serlo!

Die Skizze unten zeigt das Trapez $A B C D$ .

Es gilt: $A B = 7 cm; B C = 10 cm; A C = 14 cm$

$∢ C A D = 50^{\circ}; A B | | C D$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

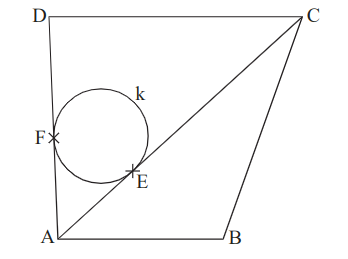
Zeichnen Sie das Trapez $A B C D$ und berechnen Sie das Maß $β$ des Winkels $C B A$ sowie das Maß $ε$ des Winkels $B A C$ .
$[$ Ergebnisse: $β = {109,62}^{\circ}; ε = {42,28}^{\circ}$ $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Lösung:
1. Berechnung der gesuchten Winkel:
Die Bezeichnung von Winkeln wird auf der Seite "Winkel" erklärt. Der Winkel $∢ C B A$ wird in der Zeichnung $β$ genannt und der Winkel $∢$ $B A C$ wird ε genannt. Der Winkel $∢ C A D = 50 °$ ist auch eingezeichnet.
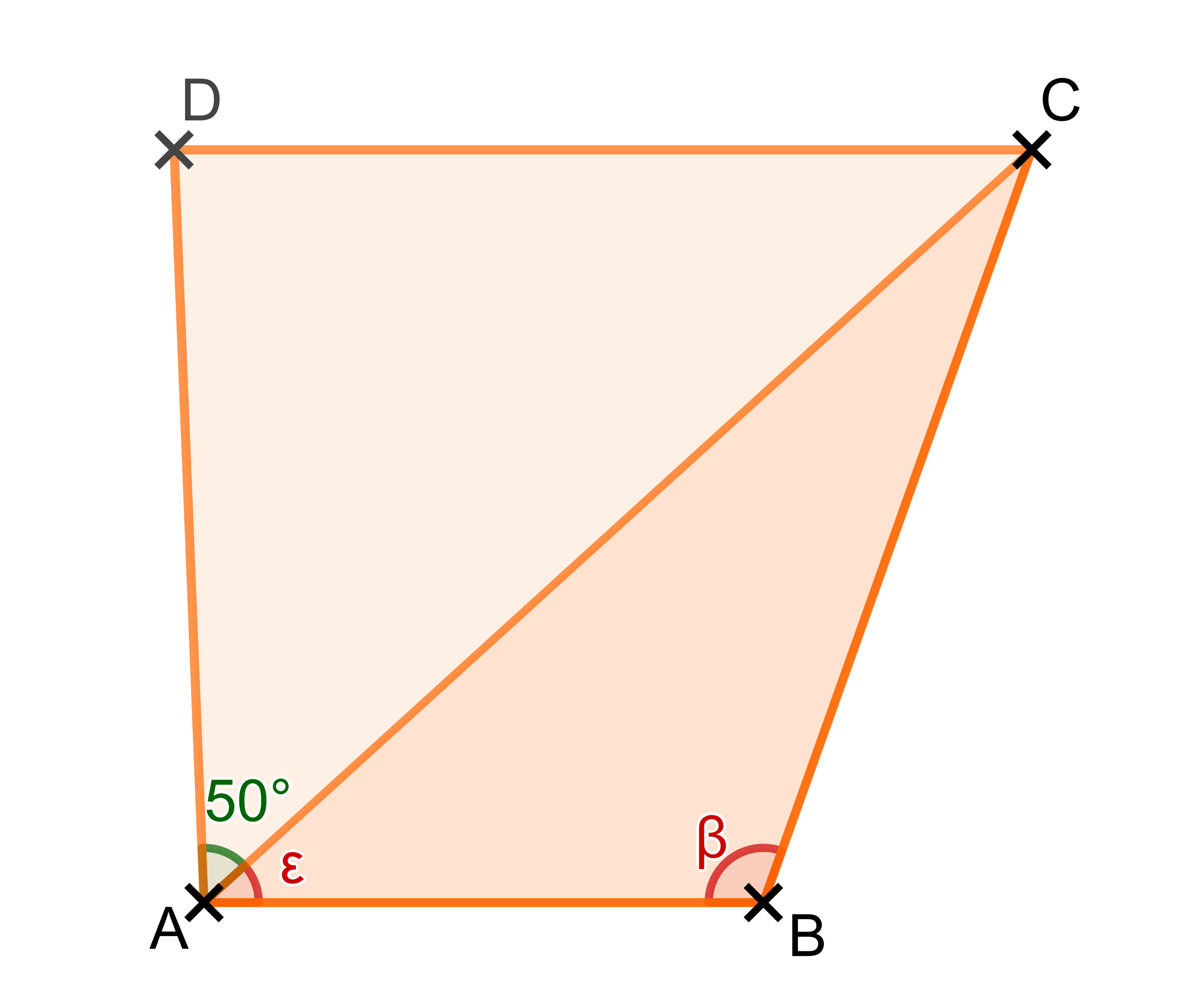
Winkel $∢ C B A = β$ :
Im Dreieck $A B C$ sind die Längen aller drei Seiten bekannt. Die Größen der Winkel sind nicht bekannt. Das Maß $β$ des Winkels $∢$ $C B A$ soll bestimmt werden.
In diesem Fall kann man den Kosinussatz verwenden:
(Der Sinussatz kommt hier nicht infrage, weil dafür mindestens ein Winkel im Dreieck $A B C$ bekannt sein müsste.)
Da $β$ berechnet werden soll, steht die Länge $A C$ der Seite, die gegenüber von $β$ ist, ganz links in der Gleichung, also $14 cm$ .
Rechts in der Gleichung setzt du die Längen der Seiten ein, die $β$ berühren, also $B C = 10 cm$ und $A B = 7 cm$ .
${A C}^{2} = {B C}^{2} + {A B}^{2} - 2 \cdot B C \cdot A B \cdot \cos (β)$
$(14 cm)^{2} = (10 cm)^{2} + (7 cm)^{2} - 2 \cdot 10 cm \cdot 7 cm \cdot \cos (β)$
Ausrechnen der Zahlenwerte:
$196 {cm}^{2} = 149 {cm}^{2} - 140 {cm}^{2} \cdot \cos (β)$
Umstellen nach $\cos (β)$ :
$\cos (β) = \frac{196 {cm}^{2} - 149 {cm}^{2}}{- 140 {cm}^{2}} = - 0,3357...$
Berechnen von $β$ mit der Umkehrfunktion $\cos^{- 1} (- 0,3357...)$ :
$β = \cos^{- 1} (- 0,3357...) = {109,62}^{\circ}$
Winkel $∢$ $B A C = ε$ :
Das Maß $ε$ des Winkels $∢$ $B A C$ kann man wieder mit dem Kosinussatz berechnen, da die Längen aller drei Seiten im Dreieck bekannt sind. Eine andere Möglichkeit ist hier die Berechnung mit dem Sinussatz. Er kann hier verwendet werden, weil $β$ bereits berechnet wurde.
Im Folgenden wird die Rechnung mit dem Sinussatz durchgeführt, da sie etwas kürzer ist.
Weil $ε$ berechnet werden soll und $β$ bekannt ist, setzen wir diese beiden Winkel in die Rechnung ein. $B C = 10 cm$ ist die Länge der Seite gegenüber von $ε$ . $A C = 14 cm$ ist die Länge der Seite gegenüber von $β$ .
$\frac{\sin (ε)}{B C} = \frac{\sin (β)}{A C}$
Einsetzen der Längen:
$\frac{\sin (ε)}{10 cm} = \frac{\sin (β)}{14 cm}$
Umstellen nach $\sin (ε)$ :
$\sin (ε) = \frac{10 cm}{14 cm} \cdot \sin (β)$
Einsetzen von $β = {109,62}^{\circ}$ :
$\sin (ε) = \frac{10 cm}{14 cm} \cdot \sin ({109,62}^{\circ}) = 0,67$
Berechnen von ε mit der Umkehrfunktion $\sin^{- 1} (0,67)$ :
$ε = \sin^{- 1} (0,67) = {42,28}^{\circ}$
2. Zeichnung des Trapezes $A B C D$ :
Mit Zirkel:
Um den Punkt $D$ zu erhalten, verwendet man die Angabe $A B | | C D$ und $∢$ $C A D$ $= α =$ $50 °$ .
$A B | | C D$ bedeutet, dass die Seite $A B$ parallel zu der Seite $C D$ ist. Der Punkt $D$ liegt also auf einer parallelen Geraden zu $A B$ durch den Punkt $C$ . Diese kannst du mit dem Zirkel konstruieren oder mit dem Geodreieck zeichnen.
Für die Zeichnung mit dem Geodreieck verlängerst du die Strecke $A B$ ein Stück (siehe Bild). Dann zeichnest du im rechten Winkel dazu eine Gerade durch den Punkt $C$ (senkrechte gestrichelte Linie). Zu dieser Gerade zeichnest du wieder im rechten Winkel eine Gerade (waagrechte gestrichelte Linie).
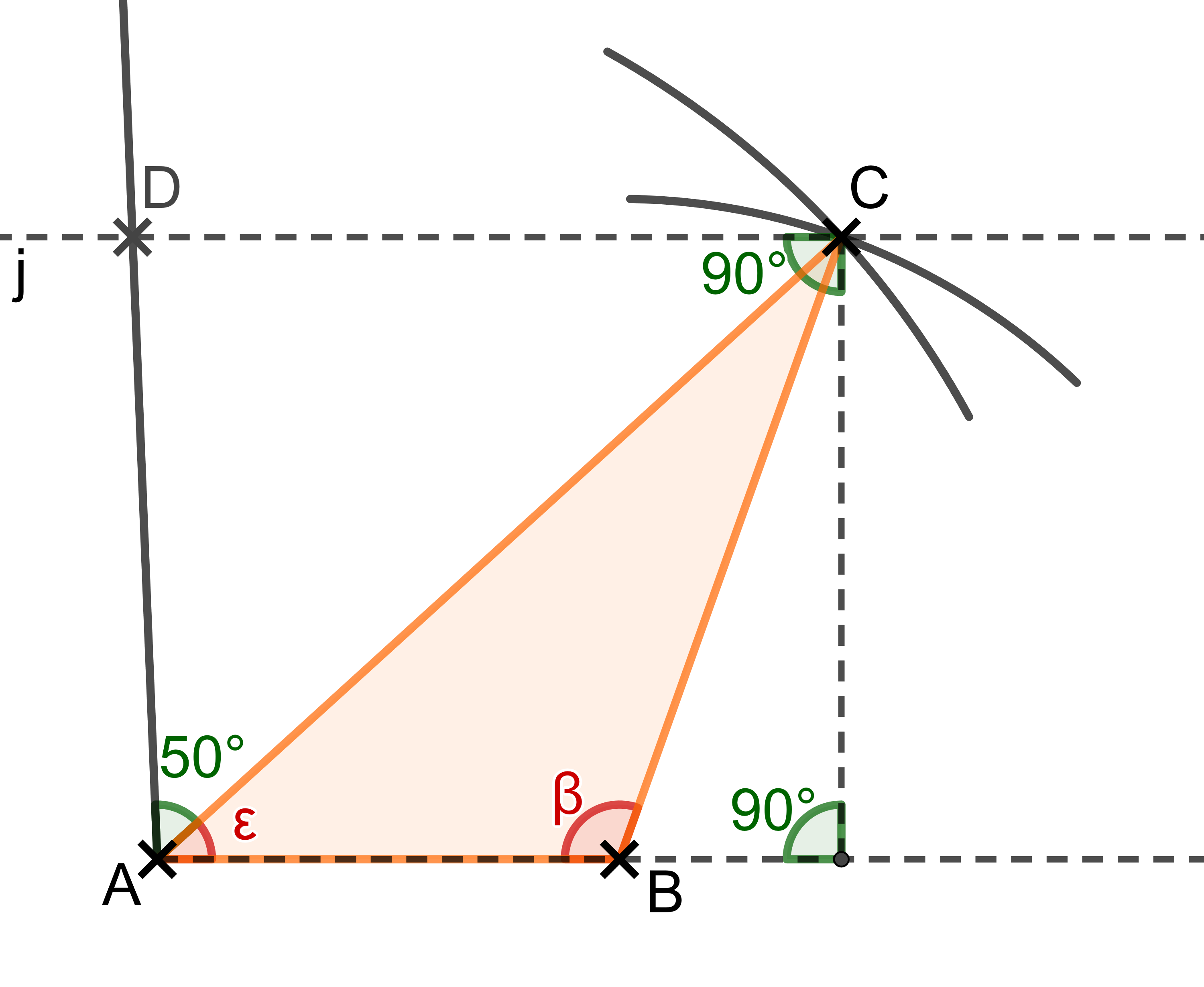
Nun zeichnest du den Winkel $∢$ $C A D = 50 °$ . Hierfür legst du das Geodreieck an der Seite $A C$ des Dreiecks an. Dann zeichnest du den fehlenden Schenkel des Winkels so lang, dass du einen Schnittpunkt mit der gestrichelten Linie erhältst.
Der Punkt $D$ ist der Schnittpunkt.
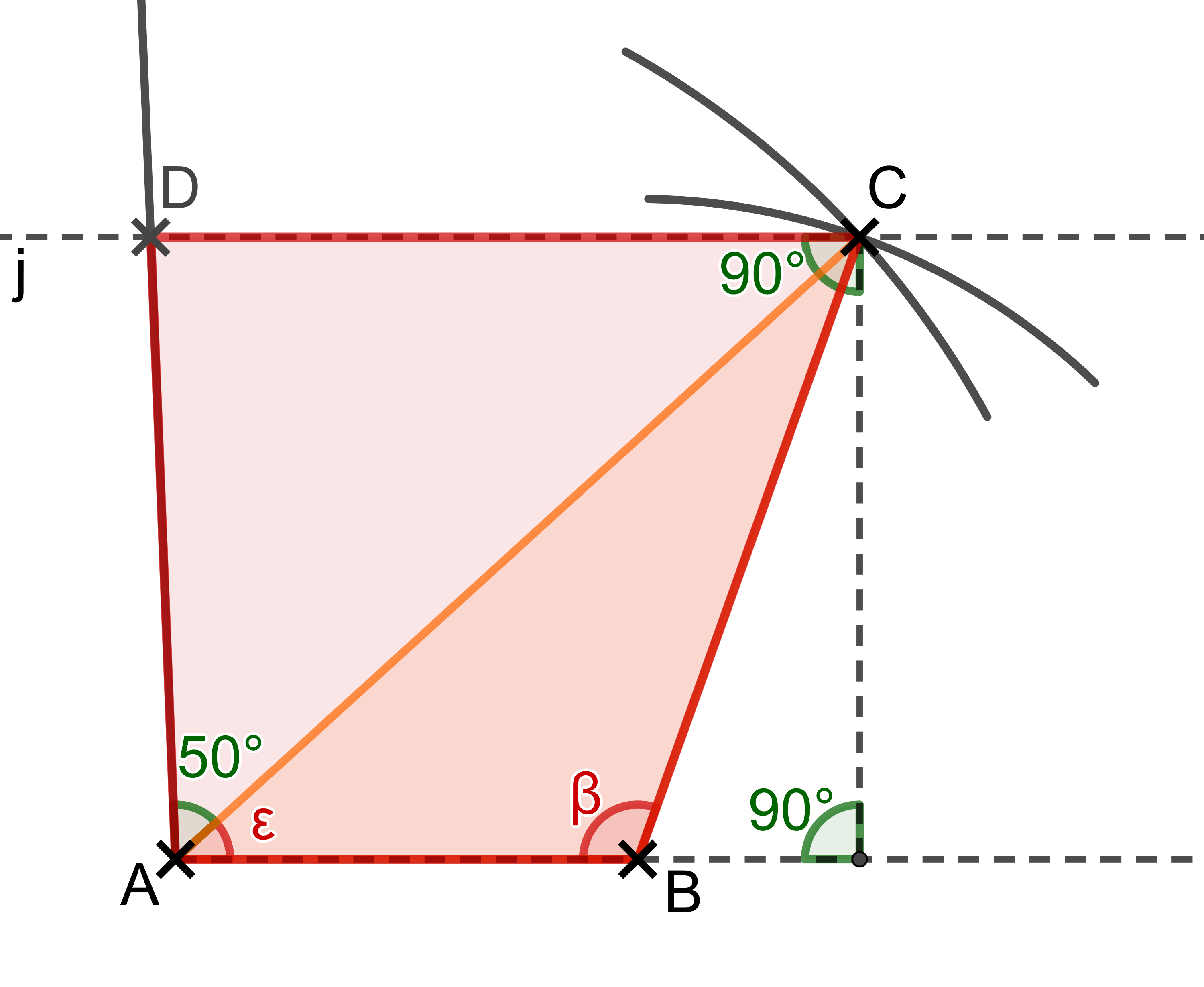
Nun verbindet man die vier Punkte $A B C D$ zu einem Trapez:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zuerst kann man die gesuchten Winkel berechnen.
Danach kann man das Trapez $A B C D$ zeichnen. Das kannst du mithilfe eines Zirkels machen oder mit den berechneten Winkeln.
Die Strecke $[B P]$ ist die kürzeste Verbindung des Punktes $B$ zur Strecke $[A C]$ . Ergänzen Sie in der Zeichnung zu Teilaufgabe a) die Strecke $[B P]$ .
Berechnen Sie sodann den Umfang $u$ des Dreiecks $A B P$ .
Lösung:
1. Bestimmung der kürzesten Verbindung des Punktes $B$ zur Strecke $[A C]$ :
Die kürzeste Verbindung steht im rechten Winkel auf $[A C]$ . Dies ist in der Graphik eingezeichnet als $[B P]$ .
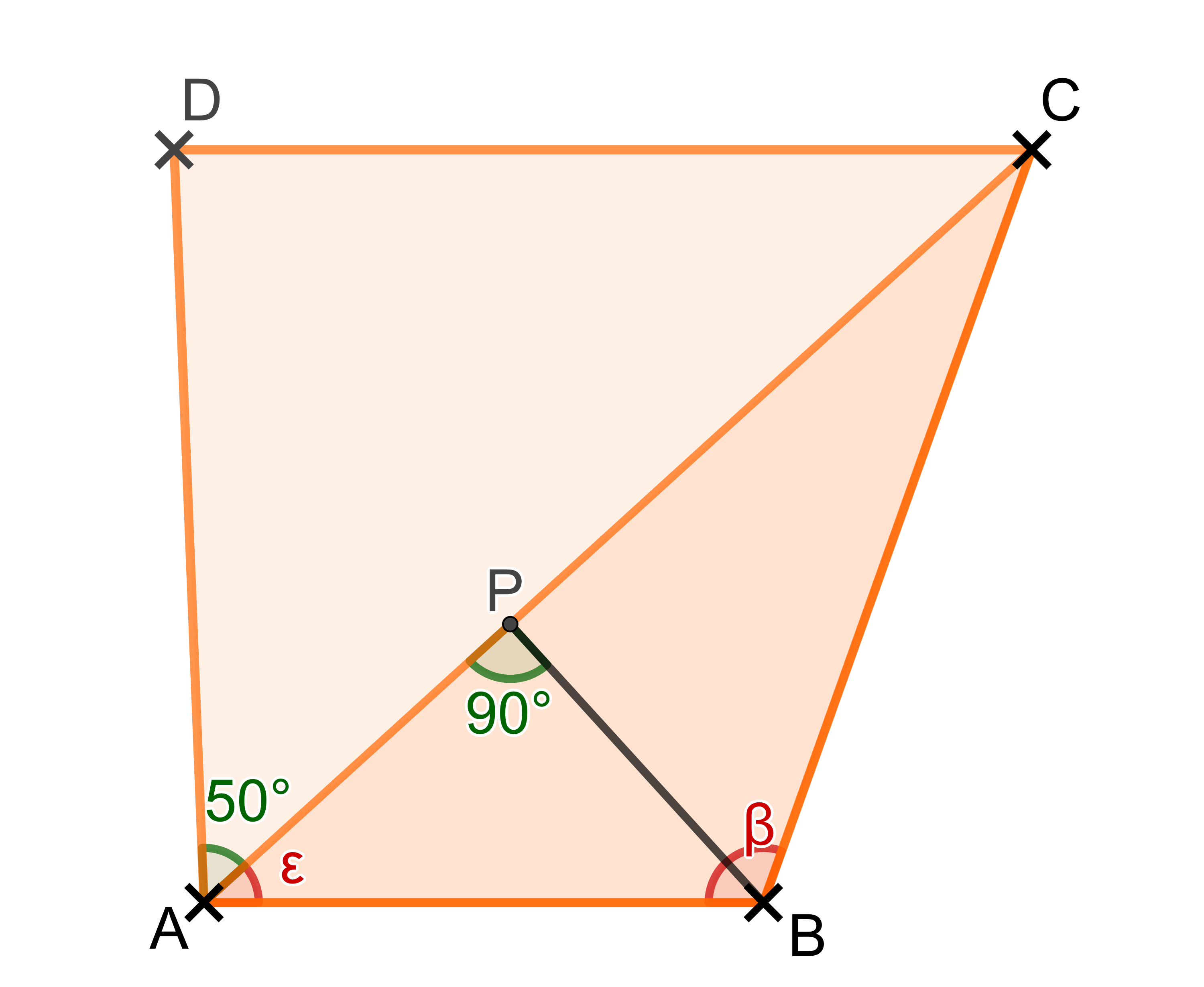
2. Berechnung des Umfangs $u$ :
Vorgehen:
Überlege dir die Formel für den Umfang des Dreiecks $A B P$ .
Welche Längen sind gegeben, welche gesucht?
Berechne die gesuchten Längen. Tipp: Überlege dir, welche Winkel bekannt sind, und nutze das Grundwissen zu Sinus und Kosinus.
Setze diese Längen in die Formel für den Umfang $u$ ein.
Lösung:
1. Formel für den Umfang des Dreiecks $A B P$ :
Den Umfang $u$ des Dreiecks $A B P$ berechnet man, indem man die Längen der drei Seiten addiert, also $A B$ , $B P$ und $A P$ .
$u_{A B P} = A B + B P + A P$
2. Gegebene und gesuchte Längen:
Du weißt aus der Angabe bereits, dass $A B = 7 cm$ ist. Die Längen $B P$ und $A P$ musst du noch berechnen.
3. Berechnung der gesuchten Längen:
Das Dreieck $A B P$ ist rechtwinklig und du kennst den Winkel $ε$ und die Länge $A B$ . Daher kannst du Sinus und Kosinus zur Berechnung verwenden.
Berechnung der Länge $B P$ :
$B P$ ist in dem rechtwinkligen Dreieck die Gegenkathete zum Winkel $ε$ und $A B$ ist die Hypotenuse. Daher kannst du die Länge $B P$ mit dem Sinus berechnen.
$\sin (ε) = \frac{Gegenkathete}{Hypotenuse} = \frac{B P}{A B}$
Umstellen nach $B P$ durch Multiplikation mit der Länge $A B$ auf beiden Seiten der Gleichung
$B P = A B \cdot \sin (ε)$
Einsetzen der Zahlen:
$B P = 7 cm \cdot \sin (42,28 °) = 4,7092... cm \approx 4,71 cm$
Berechnung der Länge von $A P$ :
$A P$ ist in dem rechtwinkligen Dreieck die Ankathete und sie schließt den Winkel $ε$ zusammen mit der Hypotenuse $A B$ ein. Daher kannst du die Länge $B P$ mit dem Kosinus berechnen.
$\cos (ε) = \frac{Ankathete}{Hypotenuse} = \frac{A P}{A B}$
Umstellen nach $A P$ durch Multiplikation mit $A B$ auf beiden Seiten der Gleichung
$A P = A B \cdot \cos (ε)$
Einsetzen der Zahlen:
$A P = 7 cm \cdot \cos (42,28 °) = 5,1790... cm \approx 5,18 cm$
4. Einsetzen in die Formel für den Umfang $u_{A B P}$ :
$u_{A B P} = A B + B P + A P = 7 cm + 4,71 cm + 5,18 cm = 16,89 cm$
Der Umfang beträgt also $16,89 cm$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege, wie du die kürzeste Verbindung zwischen dem Punkt $B$ und der Strecke $[A C]$ bestimmen kannst
Berechne des Umfang $u$ des Dreiecks $A B P$
Berechnen Sie den Flächeninhalt $A$ des Trapezes $A B C D$ .
$[$ Ergebnis: $A = 83,51 cm$ $]$
Vorgehen:
Überlege dir zuerst die Formel für den Flächeninhalt eines Trapezes.
Überprüfe, welche Längen gegeben sind und welche du noch berechnen musst.
Berechne diese Längen und setze sie in die Formel ein.
Lösung:
1. Formel für den Flächeninhalt eines Trapezes:
Der Flächeninhalt $A$ des Trapezes mit der Höhe $h$ und den parallelen Seiten $[A B]$ und $[C D]$ ist:
$A = \frac{A B + C D}{2} \cdot h$
2. Gegebene und zu berechnende Längen:
Länge, die gegeben ist:
die Länge $A B = 7 cm$
Längen, die du berechnen musst:
die Höhe $h = B J$
die Länge $C D$
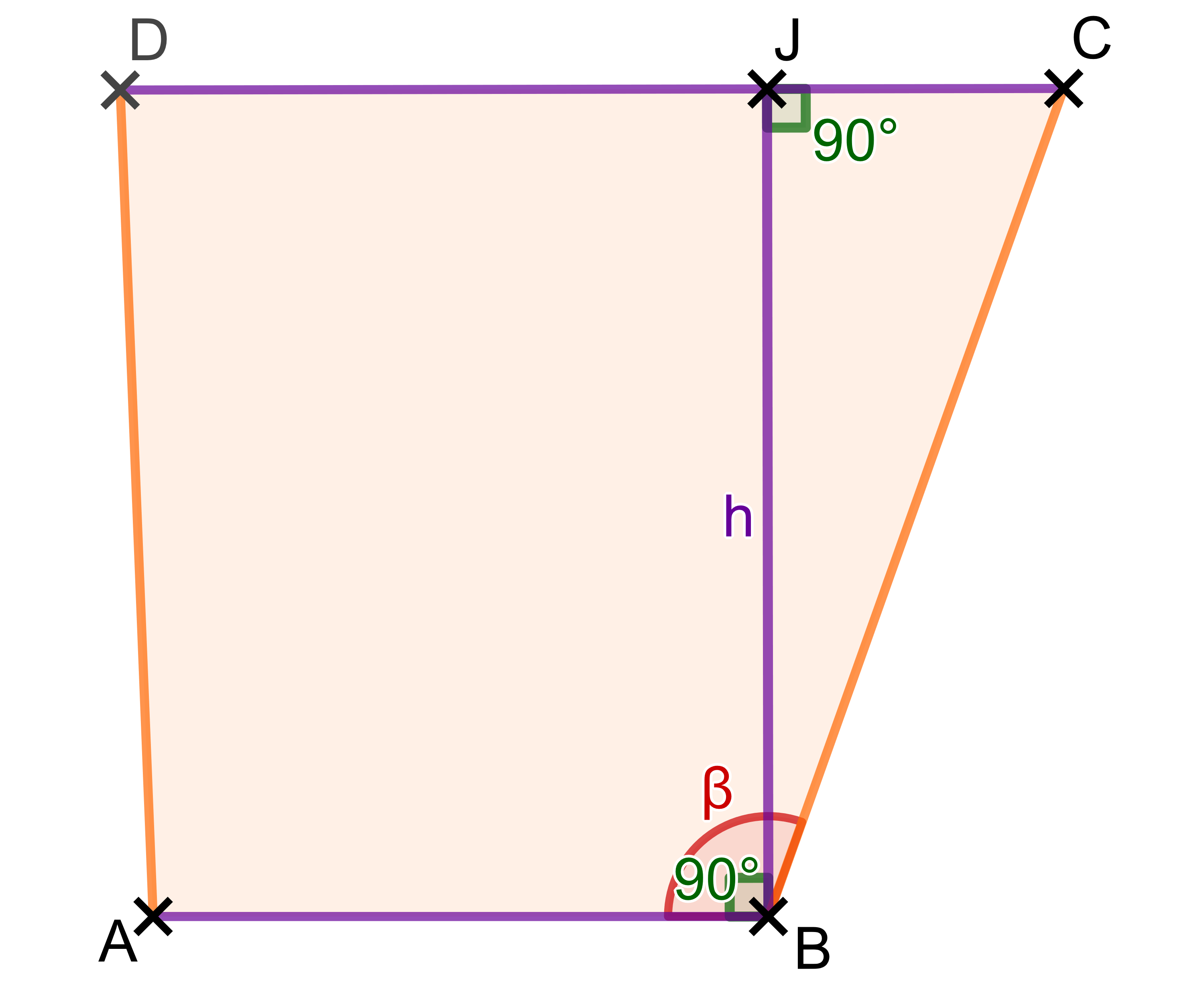
3. Berechnung der Längen und Einsetzen in die Formel
Berechnung der Höhe $h = B J$ :
Hierfür verwendet man zum Beispiel das Dreieck $B C J$ .
Da die Höhe $h$ senkrecht zu den Seiten $[A B]$ und $[C D]$ ist, ist Folgendes gegeben:
$\begin{array}{l} ∢ C B J = β - 90^{\circ} \\ = {109,62}^{\circ} - 90^{\circ} \\ = {19,62}^{\circ} \end{array}$
$∢ B J C = 90^{\circ}$
$ B C = 10 cm$
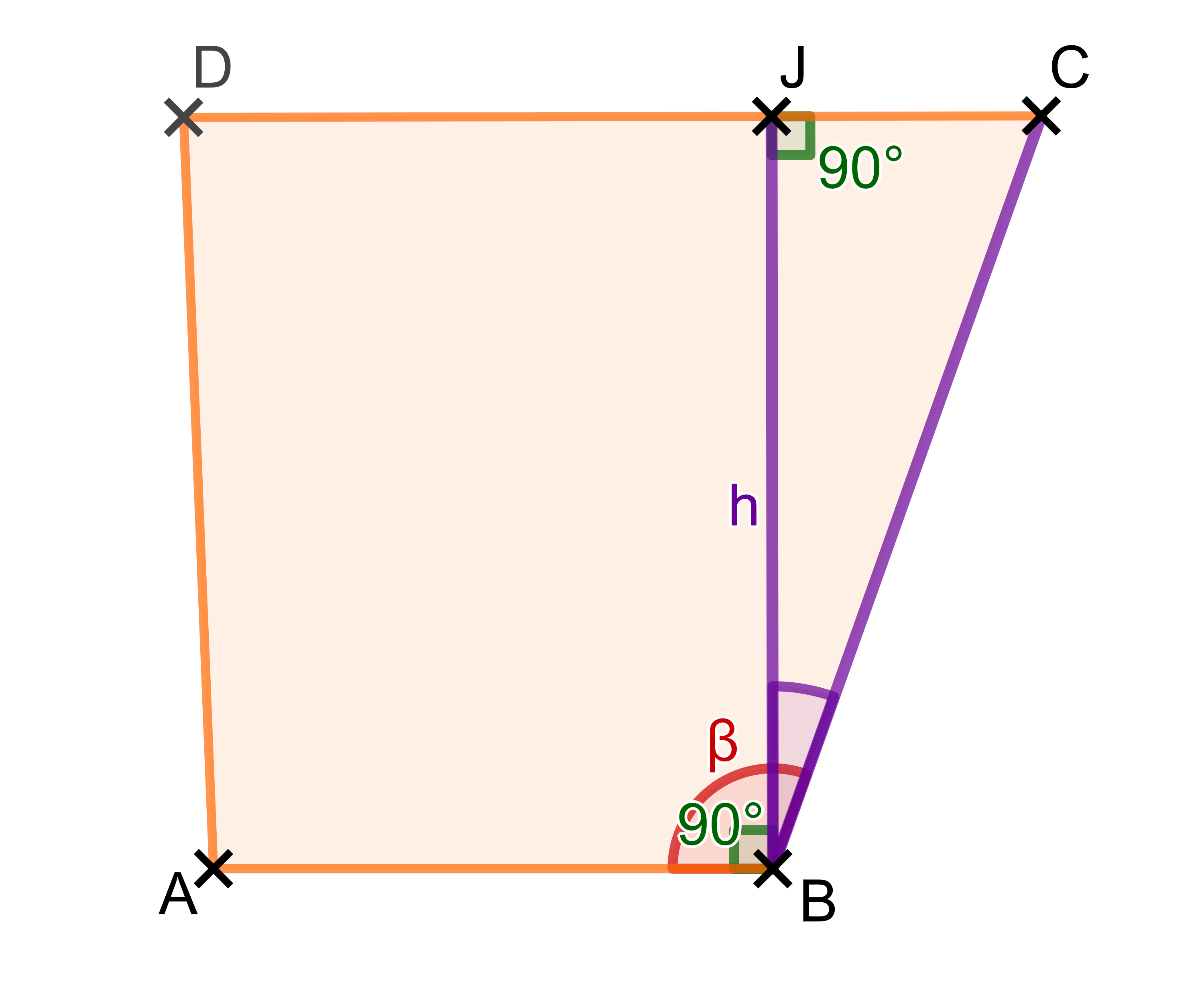
Das Dreieck ist also rechtwinklig, du kennst einen Winkel und die Länge der Hypotenuse $B C = 10 cm$ . Daher kannst du nun die Höhe $h = B J$ mit dem Kosinus berechnen.
$\begin{array}{lcl} \cos (∢ C B J) & = & \frac{Gegenkathete}{Hypotenuse} = \frac{B J}{B C} \end{array}$
Einsetzen der gegebenen Länge und des Winkels:
$\cos ({19,62}^{\circ}) = \frac{B J}{10 cm}$
Umstellen nach $B J$ durch Multiplikation mit $10 cm$ auf beiden Seiten der Gleichung:
$B J = \cos ({19,62}^{\circ}) \cdot 10 cm = 9,4194... cm \approx 9,42 cm$
Die Höhe $h = B J$ beträgt also $9,42 cm$ .
Berechnung der Länge $C D$ :
Betrachte hierfür die Zeichnung in der Aufgabenstellung.
Überlege, welches Dreieck in der Zeichnung für die Rechnung hilfreich sein könnte.
Welche Längen und Winkel sind bekannt? Musst du für die Rechnung zusätzliche Längen oder Winkel berechnen?
Welche Funktion oder welchen Satz kannst du anwenden? (z.B. Sinus, Kosinus, Tangens, Sinussatz, Kosinussatz)
Lösung:
Hilfreiches Dreieck:
Hier kann man das Dreieck $A C D$ verwenden.
Bekannte und zu berechnende Winkel:
Die Seitenlänge $A C$ und der Winkel $∢ C A D = 50 °$ sind bekannt.
Das reicht noch nicht, um die Länge $C D$ berechnen zu können, denn es ist nicht bekannt, ob das Dreieck rechtwinklig ist.
Der Winkel $∢$ $A D C$ kann aber leicht berechnet werden.
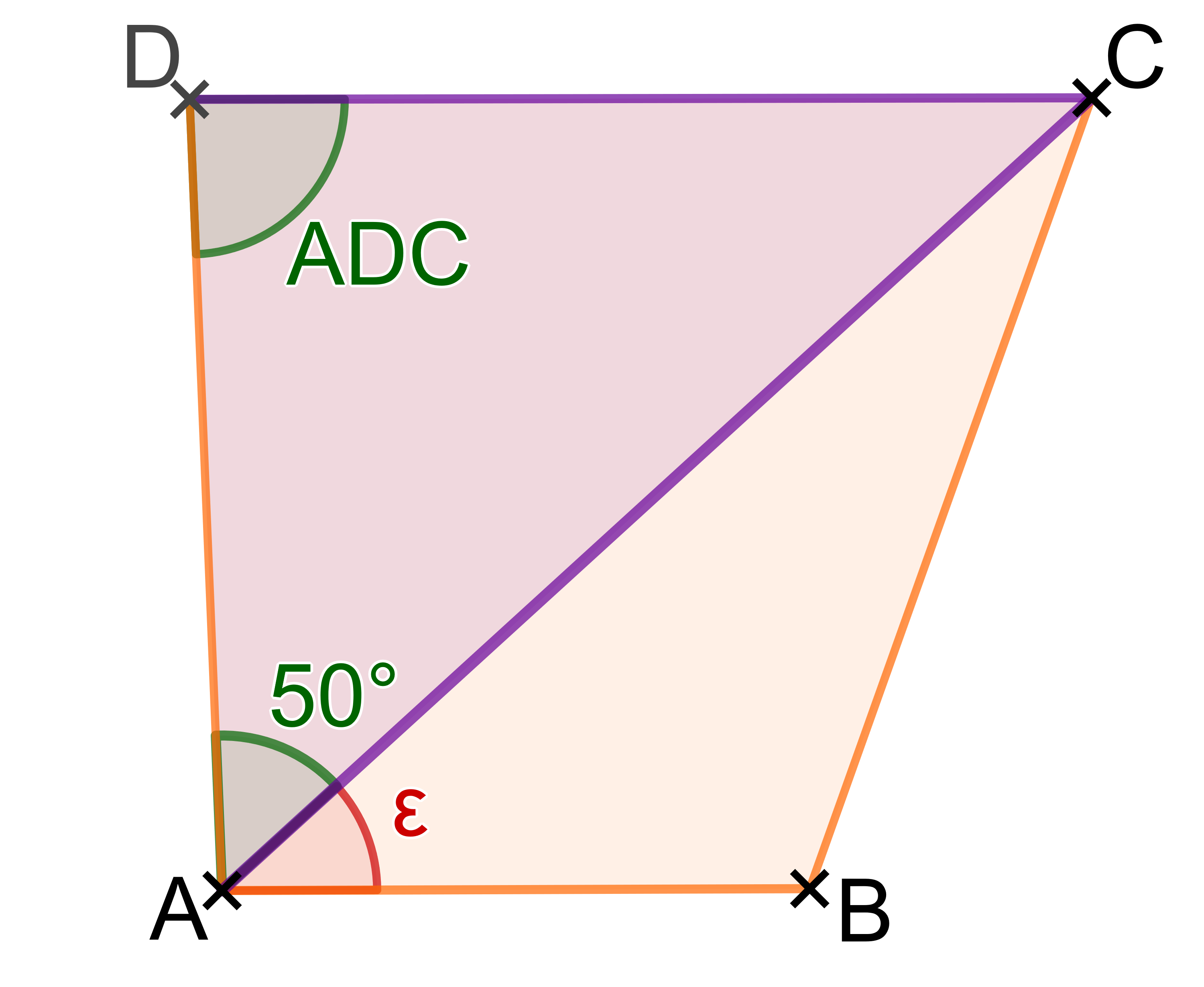
Einzeichnen des Kreises $k$ und des Mittelpunkts $M$ :
Bestimme die Lage des Mittelpunkts $M$
Zeichne mit dem Zirkel einen Kreis mit dem Radius $r = 2 cm$ Berechnung des Winkels $∢$ $A D C$ :
Die Seite $[A B]$ ist parallel zu der Seite $[C D]$ . Daraus folgt
$∢ A D C + ∢ B A D = 180^{\circ}$
Der Winkel $∢ B A D$ setzt sich aus $ ε$ und $50 °$ zusammen. Also gilt
$∢ A D C + 50^{\circ} + ε = 180^{\circ} ∢ A D C + 50^{\circ} + {42,28}^{\circ} = 180^{\circ} ∢ A D C + {92,28}^{\circ} = 180^{\circ}$
Umstellen nach $∢ A D C$ durch Abziehen von $92,28 °$ auf beiden Seiten der Gleichung:
$\begin{array}{l} ∢ A D C = {87,72}^{\circ} \end{array}$
Anwendung des Sinussatzes:
Das Dreieck ist also nicht rechtwinklig. Daher kommen für die Rechnung nur noch Sinus- oder Kosinussatz infrage. Da nur eine Seite bekannt ist, aber zwei Winkel, verwendet man hier den Sinussatz. Dabei teilst du jeweils eine Seitenlänge durch den Winkel, der gegenüber von ihr liegt
$\frac{C D}{\sin (∢ C A D)} = \frac{A C}{\sin (∢ A D C)}$
Einsetzen der bekannten Längen und Winkel:
$\frac{C D}{\sin (50^{\circ})} = \frac{14 cm}{\sin ({87,72}^{\circ})} = 14,0110... cm$
Umstellen nach $C D$ durch Multiplikation mit $\sin (50 °)$
$\begin{array}{l} C D = 14,0110... cm \cdot \sin (50^{\circ}) = 10,7330... cm \approx 10,73 cm \end{array}$
Berechnung des Flächeninhalts $A$ des Trapezes durch Einsetzen der Längen in die Formel:
$A = \frac{A B + C D}{2} \cdot h A = \frac{7 cm + 10,73 cm}{2} \cdot 9,42 cm = 83,5083 {cm}^{2} \approx 83,51 {cm}^{2}$
Das Trapez hat also eine Fläche von $83,51 {cm}^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege dir zuerst die Formel für den Flächeninhalt eines Trapezes.
Überprüfe, welche Längen gegeben sind und welche du noch berechnen musst.
Berechne diese Längen und setze sie in die Formel ein.
Der Kreis $k$ mit dem Mittelpunkt $M$ berührt die Strecke $[A C]$ im Punkt $E$ und die Strecke $[A D]$ im Punkt $F$ . Für den Radius $r$ gilt: $r = M E = M F = 2 cm$ .
Ergänzen Sie in der Zeichnung zu Teilaufgabe a) den Kreis $k$ mit dem Mittelpunkt $M$ . Berechnen Sie sodann den prozentualen Anteil des Flächeninhalts des Kreises $k$ am Flächeninhalt des Trapezes $A B C D$ .
Lösung:
1. Bestimmung der Lage des Mittelpunkts $M$ :
Betrachte das Bild aus der Angabe:
Der Mittelpunkt $M$ hat den gleichen Abstand zu den Punkten $E$ und $F$ des Kreises. Daher hat er auch den gleichen Abstand zu den Seiten $[A C]$ und $[A D]$ . Deshalb liegt er auf der Winkelhalbierenden des Winkels $∢$ $C A D = 50 °$ .
Der Winkel $∢$ $E A M$ ist also halb so groß wie $∢$ $C A D$ . Es gilt
$∢ E A M = \frac{∢ C A D}{2} = \frac{50^{\circ}}{2} = 25^{\circ}$
Du siehst den Winkel $25 °$ in der untenstehenden Grafik eingezeichnet.
Nun kannst du den Abstand $A M$ berechnen.
Dafür stellst du dir das Dreieck $A E M$ vor.
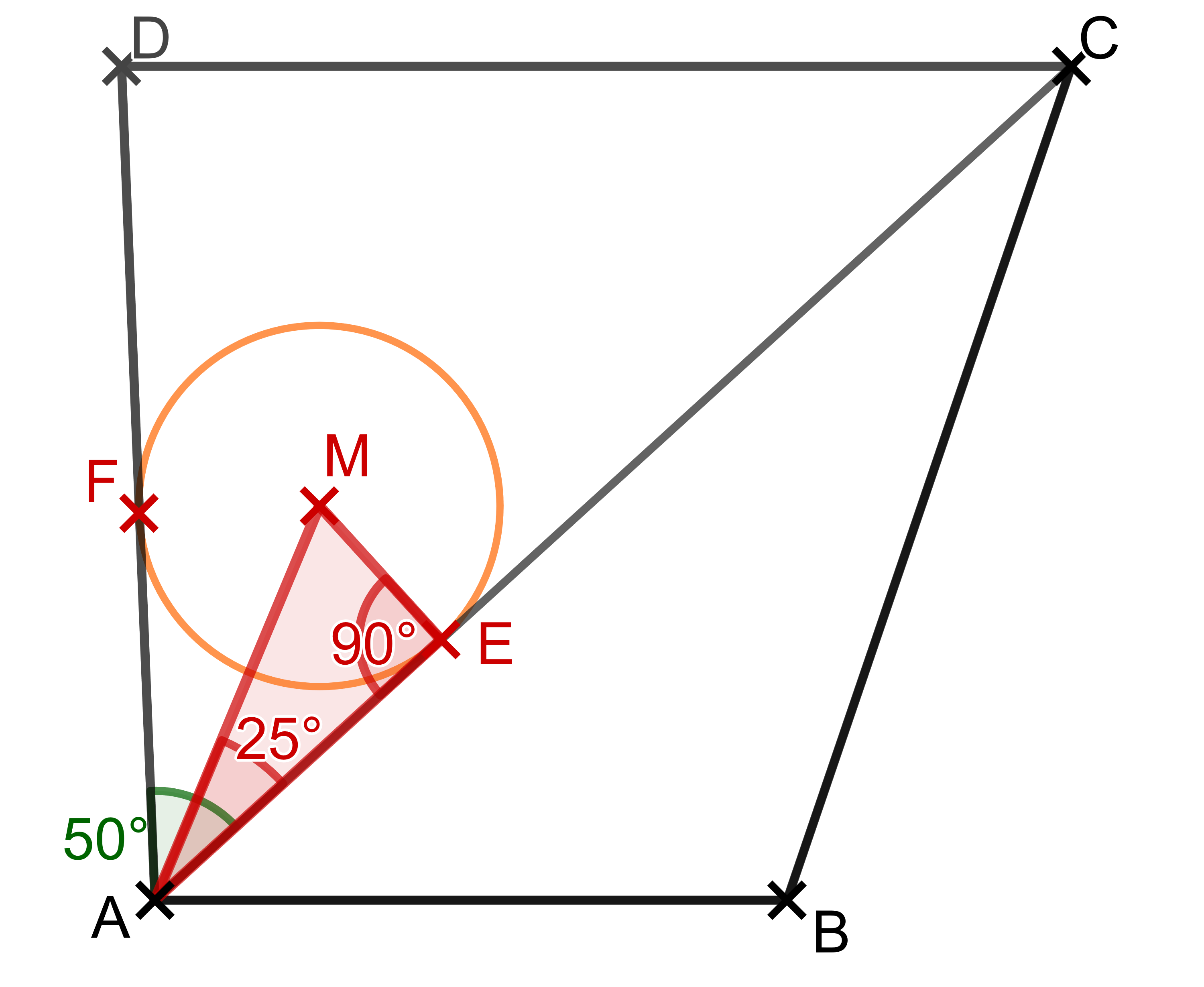
Das Dreieck $A E M$ ist rechtwinklig, weil $[A C]$ eine Tangente an den Kreis $k$ ist und diese immer im rechten Winkel zum Radius steht. Deshalb kann mit dem Sinus gerechnet werden.
$\sin (∢ E A M) = \frac{Gegenkathete}{Hypotenuse} = \frac{E M}{A M}$
Einsetzen von $∢$ $E A M = 25 °$ und $E M$ $= r = 2 cm$ :
$\sin (25 °) = \frac{2 cm}{A M}$
Umstellen nach $A M$ :
Multiplikation mit $A M$ :
$\sin (25 °) \cdot A M = 2 cm$
Division durch $\sin (25 °)$ :
$A M = \frac{2 cm}{\sin (25 °)} = 4,7324... cm \approx 4,73 cm$
Beginne nun bei Punkt $A$ und miss die Länge $4,73 cm$ entlang der Winkelhalbierenden ab. So erhältst du den Mittelpunkt $M$ .
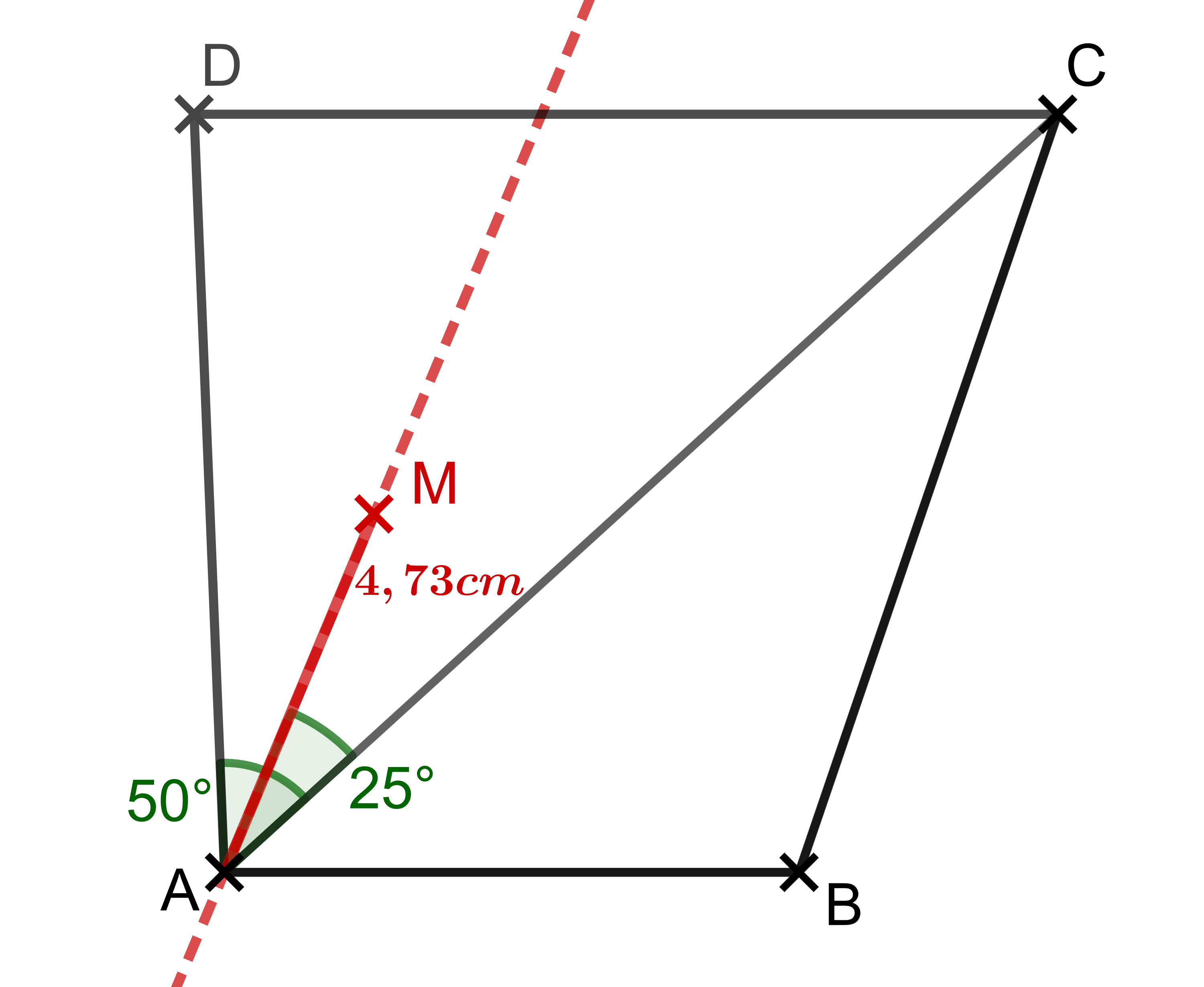
2. Einzeichnen des Kreises $k$ :
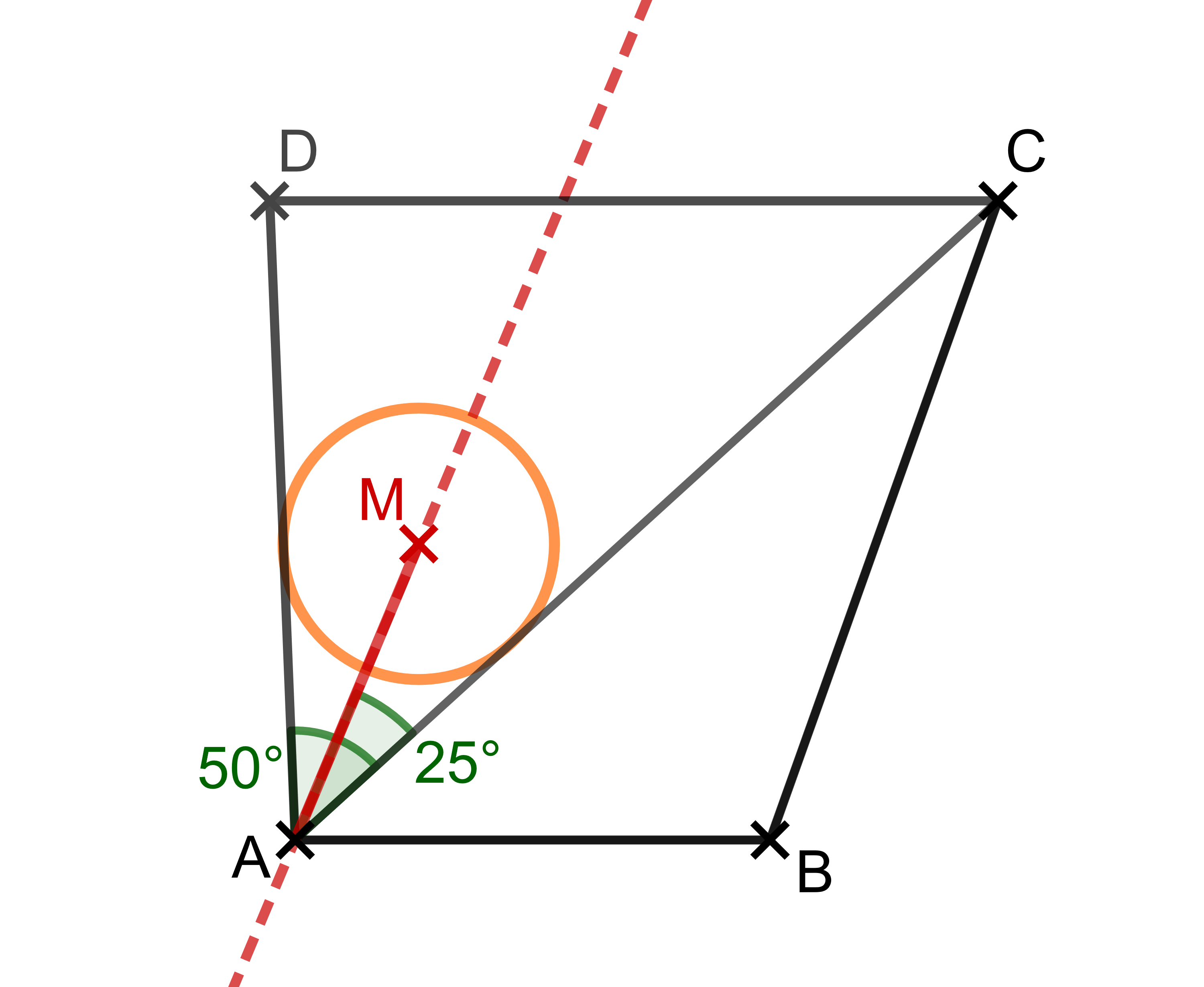
Stich nun mit dem Zirkel im Mittelpunkt $M$ ein und zeichne einen Kreis mit dem Radius $r = 2 cm$ .
Zur Kontrolle: Du hast richtig gezeichnet, wenn der Kreis die Seiten $[A C]$ und $[A D]$ berührt, aber nicht schneidet.
Berechnung: Anteil des Flächeninhalts des Kreises am Trapez
Vorgehen:
Berechne den Flächeninhalt des Kreises $k$
Berechne den prozentualen Anteil
Lösung:
1. Berechnung Flächeninhalt Kreis $k$ :
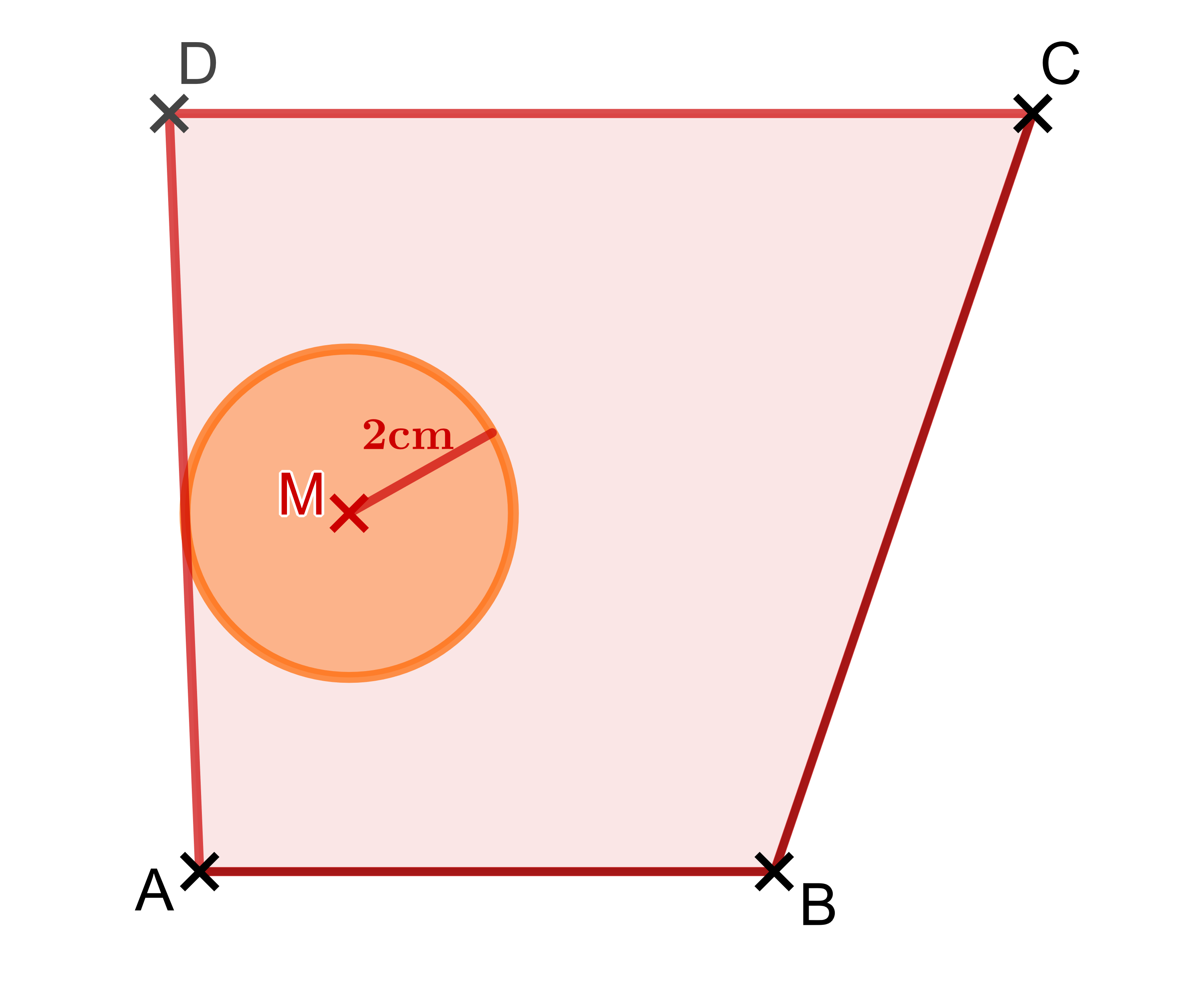
Die Formel für den Flächeninhalt eines Kreises ist
$A_{K r e i s} = π \cdot r^{2} = π \cdot {(2 cm)}^{2} = 12,5663... {cm}^{2} \approx 12,57 {cm}^{2}$
2. Berechnung prozentualer Anteil:
Für die Berechnung des prozentualen Anteils musst du dir überlegen, was der Grundwert $G$ und der Prozentwert $W$ ist. Diese Werte hast du schon ausgerechnet.

Der $Grundwert$ $G$ ist der Flächeninhalt $A$ des Trapezes $A B C D$ , also
$G = A = 83,51 {cm}^{2}$
Der $Prozentwert$ $W$ ist der Flächeninhalt $A_{K r e i s}$ des Kreises $k$ , also
$W = A_{K r e i s} = 12,57 {cm}^{2}$
Für den prozentualen Anteil, also den $Prozentsatz$ $p$ gilt nun
$Prozentsatz p = \frac{Prozentwert W}{Grundwert G} p = \frac{W}{G}$
Nun kannst du die Werte für $W$ und $G$ einsetzen
$p = \frac{12,57 {cm}^{2}}{83,51 {cm}^{2}} = 0,150520... = 15,0520... % \approx 15,05 %$
Der prozentuale Anteil des Flächeninhalts des Kreises $k$ am Flächeninhalt des Trapezes $A B C D$ ist also $15,05 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Einzeichnen des Kreises $k$ und des Mittelpunkts $M$ :
Bestimme die Lage des Mittelpunkts $M$
Zeichne mit dem Zirkel einen Kreis mit dem Radius $r = 2 cm$
Berechnen Sie den Flächeninhalt der Figur, die durch die Strecken $[A E]$ und $[A F]$ sowie den Kreisbogen $\overset{⌢}{F}$ mit dem zugehörigen Mittelpunkt $M$ begrenzt wird.
Lösung:
1. Ergänzen der Figur zu einem Drachenviereck:
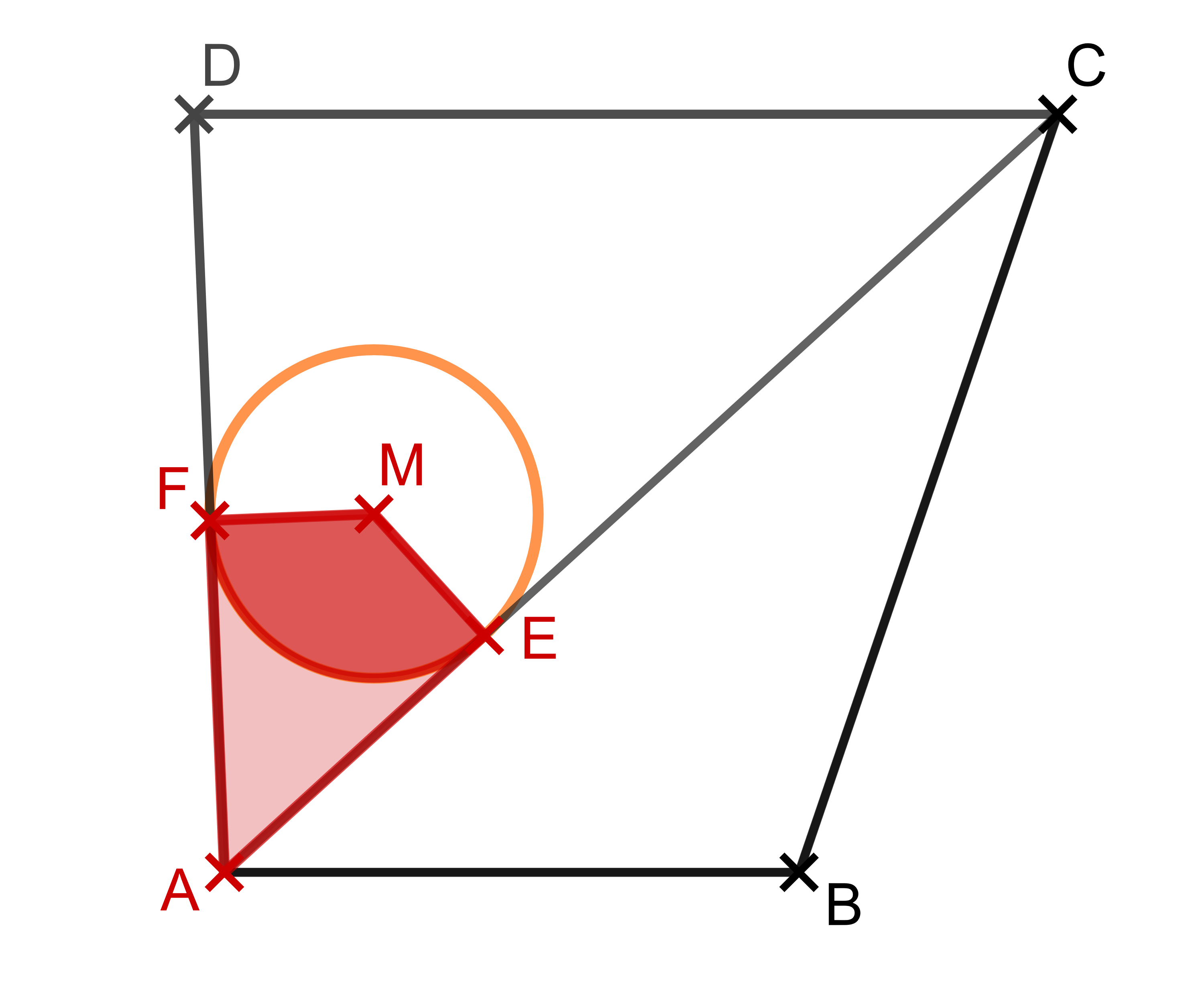
Die Fläche kann zu einem Drachenviereck ergänzt werden. Dies geschieht, indem ein Kreissektor des Kreises $k$ hinzugefügt wird.
Die gesuchte Fläche erhältst du dann, indem du von der Fläche des Drachenvierecks die Fläche des Kreissektors abziehst.
2. Berechnung der Flächeninhalte von Drachenviereck und Kreissektor:
Berechnung Flächeninhalt Drachenviereck:
Da das Drachenviereck symmetrisch zu der Achse $[A M]$ ist, ist sein Flächeninhalt doppelt so groß wie der des Dreiecks $A E M$ . Also gilt
$A_{□} = 2 \cdot A_{△}$

Für den Flächeninhalt des Dreiecks gilt
$A_{△} = \frac{1}{2} \cdot G \cdot h = \frac{1}{2} \cdot A E \cdot E M = \frac{1}{2} \cdot A E \cdot 2 cm$
Das Ergebnis kann man nun in die Gleichung für $A_{□}$ einsetzen
$A_{□} = 2 \cdot \frac{1}{2} \cdot A E \cdot 2 cm = A E \cdot 2 cm$
Als Nächstes musst du noch die Länge $A E$ berechnen:
Hierfür ist wichtig, dass das Dreieck $A E M$ rechtwinklig ist. Das heißt, dass du Sinus, Kosinus und Tangens verwenden kannst.
In der Teilaufgabe d hast du schon den Winkel $∢$ $E A M = 25 °$ berechnet. Diesen kannst du nun verwenden. Denn $[A M]$ ist die Hypotenuse des Dreiecks und sie schließt zusammen mit der gesuchten Länge $A E$ den Winkel $∢$ $E A M$ ein. Die Länge $A E$ ist also die Ankathete. Außerdem ist die Länge $E M = 2 cm$ gegeben. Das ist die Gegenkathete.
Daher kannst du die Länge $A E$ mit dem Tangens berechnen
$\tan (∢ E A M) = \frac{Gegenkathete}{Ankathete} = \frac{E M}{A E}$
Nun setzt du die Werte ein:
$\tan (25 °) = \frac{2 cm}{A E}$
Jetzt musst du die Gleichung nur noch nach $A E$ umstellen. Hierfür multiplizierst du beide Seiten mit $A E$ und teilst durch $\tan (25 °)$ . So erhältst du
$A E = \frac{2 cm}{\tan (25 °)} = 4,2890... cm \approx 4,29 cm$
Einsetzen in die Formel für den Flächeninhalt des Drachenvierecks $A_{□}$ liefert das Ergebnis
$A_{□} = A E \cdot 2 cm = 4,29 cm \cdot 2 cm = 8,58 {cm}^{2}$
Berechnung Flächeninhalt Kreissektor:
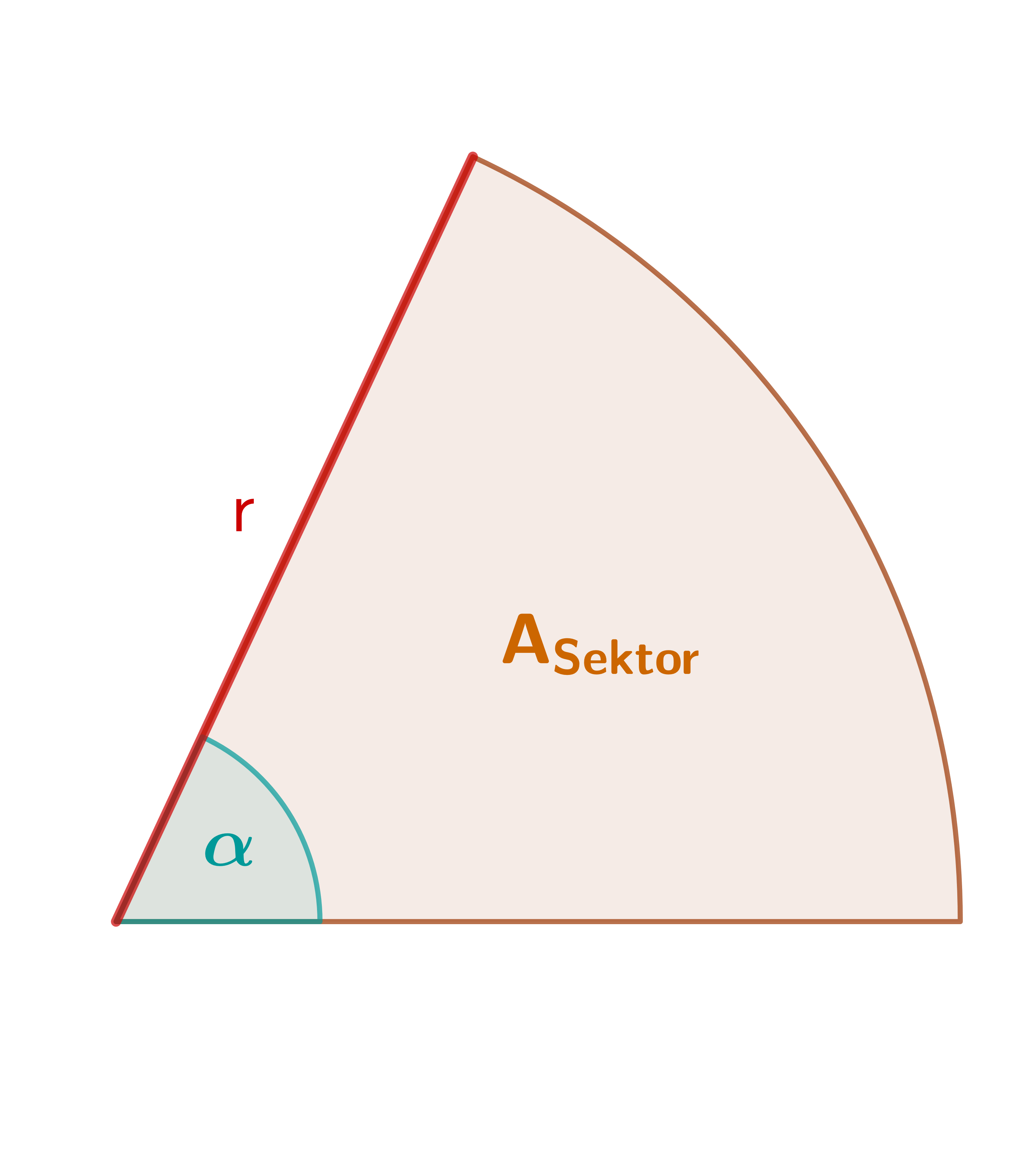
Das Verhältnis zwischen dem Flächeninhalt des Kreissektors $A_{S e k t o r}$ und dem des Kreises $A_{K r e i s}$ ist genauso groß wie das Verhältnis zwischen dem Mittelpunktswinkel $α$ und dem Gesamtwinkel $360 °$ .
$\frac{A_{S e k t o r}}{A_{K r e i s}} = \frac{α}{360 °}$
Umstellen nach $A_{S e k t o r}$ durch Multiplikation mit $A_{K r e i s}$
$A_{S e k t o r} = \frac{α}{360 °} \cdot A_{K r e i s}$
Überlege dir, wie groß der Mittelpunktswinkel $α$ ist. Orientiere dich hierfür wieder an dem Drachenviereck.
Den Mittelpunktswinkel $α$ erhältst du, indem du von der Innenwinkelsumme $360 °$ des Drachenvierecks die Größen der anderen drei Winkel abziehst, also zweimal $90 °$ und einmal $∢ C A D = 50 °$ .
$α = 360 ° - 90 ° - 90 ° - 50 ° = 130 °$
Der Flächeninhalt $A_{K r e i s}$ des Kreises mit dem Radius $r = 2 cm$ ist
$A_{K r e i s} = π \cdot r^{2} = π \cdot (2 cm)^{2} = π \cdot 4 {cm}^{2}$
Nun kannst du den Flächeninhalt $A_{K r e i s}$ und den Mittelpunktswinkel $α$ in die Formel für den Flächeninhalt $A_{S e k t o r}$ des Kreissektors einsetzen
$A_{S e k t o r} = \frac{α}{360 °} \cdot A_{K r e i s} = \frac{130 °}{360 °} \cdot π \cdot 4 {cm}^{2} = \frac{13}{9} π {cm}^{2} \approx 4,54 {cm}^{2}$
3. Berechnung Flächeninhalt gesuchte Figur
Den Flächeninhalt der gesuchten Figur kannst du jetzt ausrechnen.
Dafür ziehst du von dem Flächeninhalt des Drachenvierecks den Flächeninhalt des Kreissektors ab.
$A_{F i g u r} = A_{□} - A_{S e k t o r} = 8,58 {cm}^{2} - 4,54 {cm}^{2} = 4,04 {cm}^{2}$
Der Flächeninhalt der Figur, die durch die Strecken $[A E]$ und $[A F]$ sowie den Kreisbogen begrenzt wird, beträgt also $4,04 {cm}^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege, wie du die Figur zu einer geometrischen Fläche ergänzen kannst, die du berechnen kannst.
Berechne den Flächeninhalt dieser Fläche und den Flächeninhalt des Stücks, das du ergänzt hast.
Ziehe den Flächeninhalt des ergänzten Stücks von der Figur ab und berechne so die gesuchte Fläche