Durch Umstellen der Gleichung erhältst du $\overline{MS} = \dfrac{\overline{AM}}{\tan\left(\varphi\right)}$. Nun kannst du die Werte für $\overline{AM}$ und $\varphi$ einsetzen. Die Lösung ist dann:

Die Strecke $\overline{MS}$ hat also die Länge $73{,}2\ \text{cm}$.

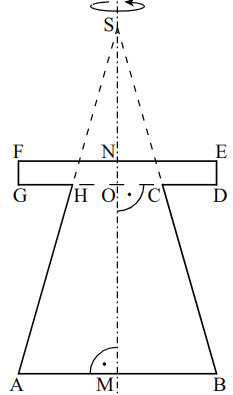
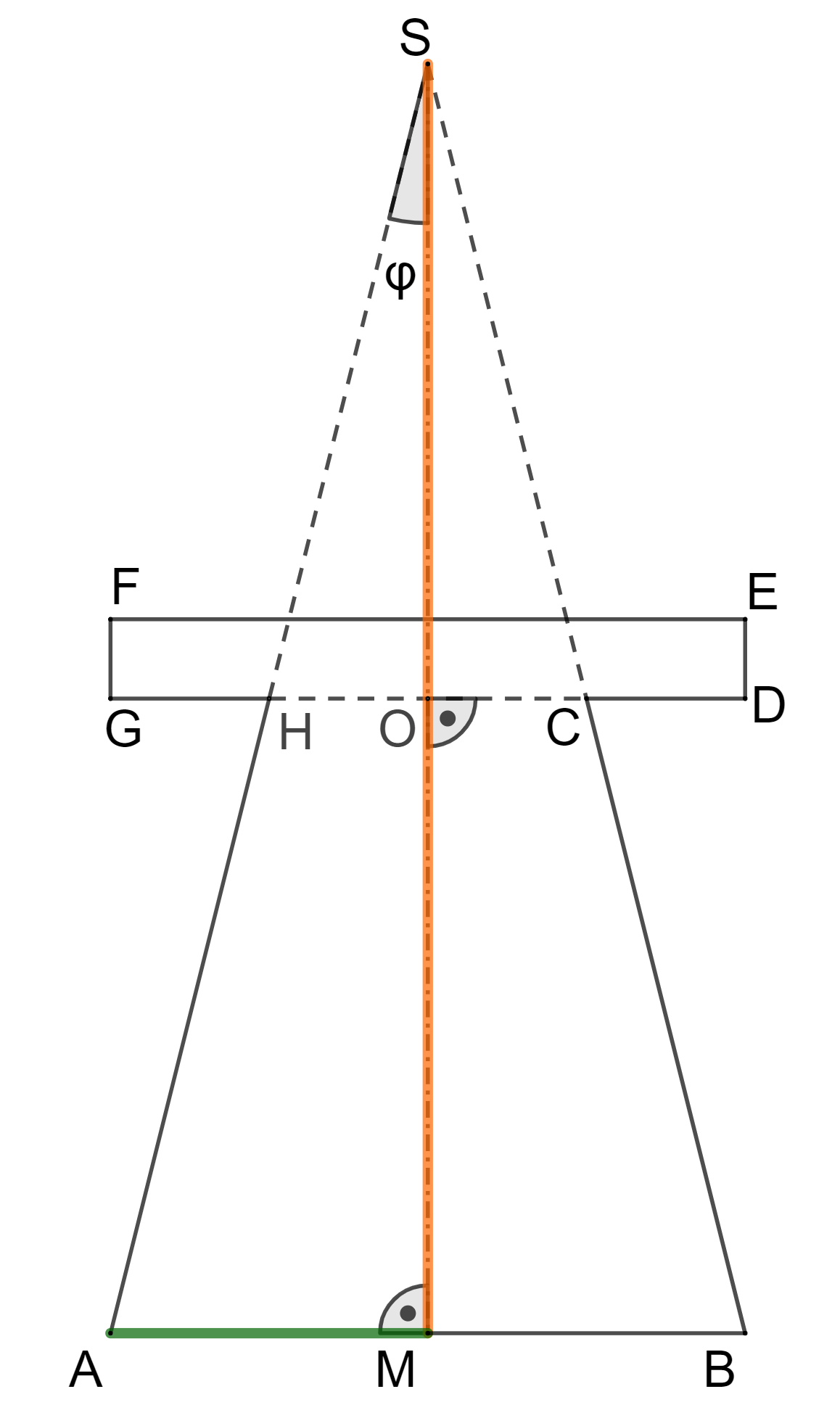
Nun kannst du noch die Länge von $\overline{HC}$ berechnen, dazu verwendest du den 2.Strahlensatz für V-Figuren.

Mit dem Strahlensatz gilt nämlich:

$\overline{HO}$ ist halb so lang wie $\overline{HC}$ und den Wert von $\overline{HO}$ kannst du bestimmen, indem du die Gleichung danach auflöst:

Durch das Umstellen der Gleichung erhältst du $\overline{HO} = \dfrac{\overline{AM}\cdot\overline{OS}}{\overline{MS}}$.

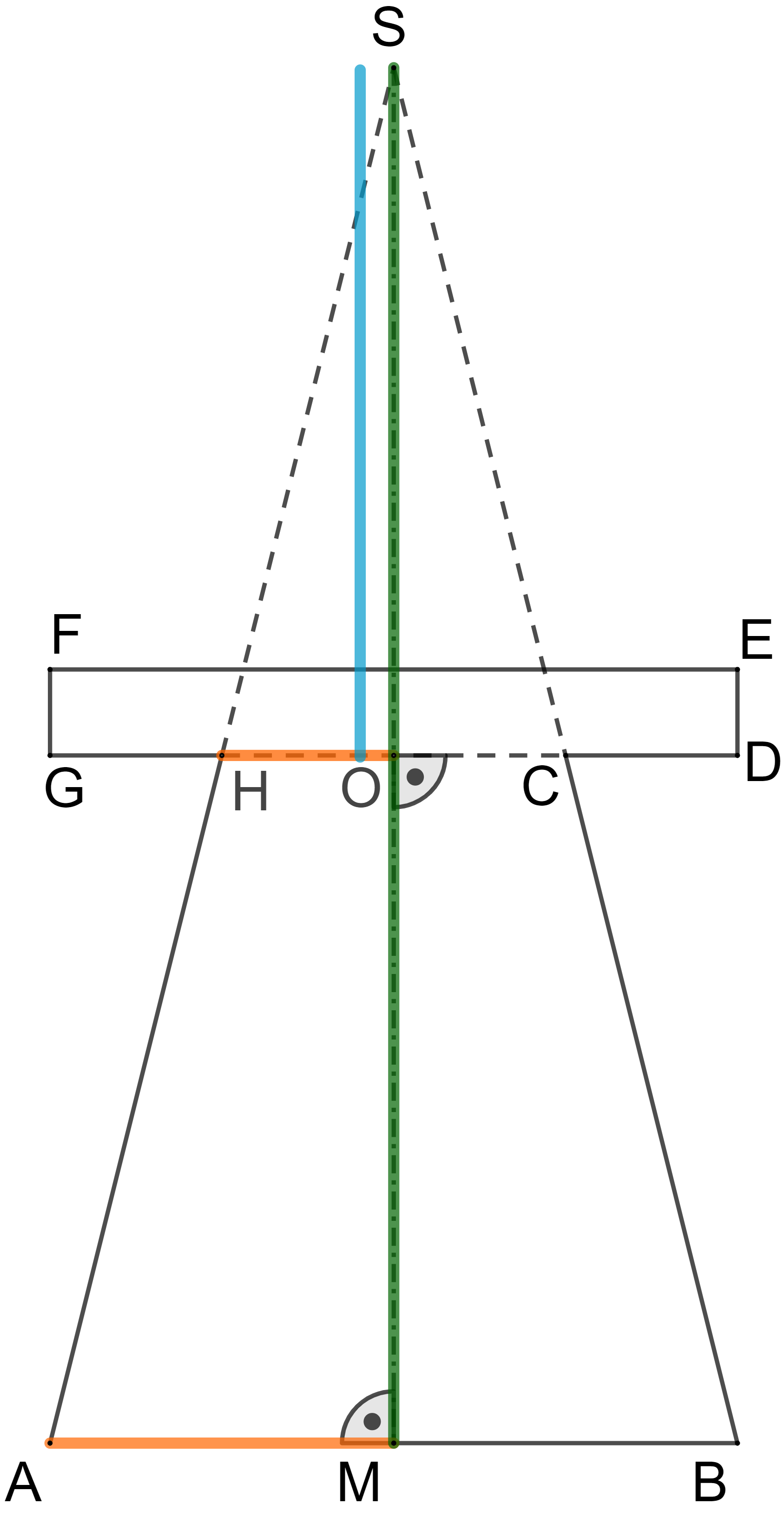
Den Wert $\overline{AM} = 21\ \text{cm}$ kennst du bereits aus der Angabe, $\overline{MS} = 73{,}2\ \text{cm}$ hast du gerade berechnet. Jetzt fehlt dir nur noch der Wert für $\overline{OS}$, dafür kannst du die Strecke $\overline{MS}$ in zwei Teilstücke aufteilen: $\overline{MS}=\overline{OS}+\overline{MO}$.

Die Strecke $\overline{MO}$ ist $5\ \text{cm}$ kürzer als $\overline{MN}$ (wegen $\overline{NO} = \overline{FG} = 5\ \text{cm}$), also gilt: $\overline{MO}=40\ \text{cm}$, damit hast du also auch $\overline{OS} = 73{,}2\ \text{cm} - 40 \ \text{cm}= 33{,}2\ \text{cm}$.

Zum Schluss kannst du jetzt die Werte einsetzen und erhältst:

Wenn du diesen Wert noch mit $2$ multiplizierst hast du das Ergebnis $\overline{HC} = 2\cdot\overline{HO} = 19\ \text{cm}.$

Das Volumen $V$des Rotationskörpers setzt sich zusammen aus dem Volumen $V_K$ des Kegelstumpfs, der durch Rotation des Trapezes $ABCH$ entsteht, und dem Volumen $V_Z$ des Zylinders, der durch Rotation des Rechtecks $GDEF$ entsteht.

Zylinder

Der Radius des Zylinders ist $\overline{GO} = 21 \ \text{cm}$ und seine Höhe beträgt $\overline{FG} = 5 \ \text{cm}$. Damit kannst du sein Volumen berechnen:

$V_{\text{Zylinder}}=\pi\cdot r^2\cdot h=\pi\cdot (21 \ \text{cm})^2\cdot 5 \ \text{cm}=6927{,}2 \ \text{cm}^3$

Kegelstumpf

Um das Volumen des Kegelstumpfs zu berechnen, kannst du das Volumen $V_{\text{kleiner Kegel}}$ des kleinen Kegels (Rotation von $HCS$) vom Volumen $V_{\text{gesamter Kegel}}$ des gesamten Kegels (Rotation von $ABS$) abziehen.

Der kleine Kegel hat den Radius $\overline{HO}= 9{,}5\ \text{cm}$ und die Höhe $\overline{OS}=33{,}2\ \text{cm}$.

Der gesamte Kegel hat den Radius $\overline{AM}=21\ \text{cm}$ und die Höhe $\overline{MS}=73{,}2\ \text{cm}$.

Durchs Einsetzen der Werte erhältst du:

$\def\arraystretch{2} \begin{array}{lll} V_K &=& V_{\text{gesamter Kegel}} - V_{\text{kleiner Kegel}} \\ \\ &=& \dfrac13\cdot \pi\cdot\left(21\ \text{cm}\right)^2\cdot73{,}2\ \text{cm} - \dfrac13\cdot\pi\cdot\left(9{,}5\ \text{cm}\right)^2\cdot33{,}2\ \text{cm} \\\\ &=& 33804{,}8\ \text{cm}^3 - 3137{,}7\ \text{cm}^3 = 30667{,}1\ \text{cm}^3 \end{array}$

Rotationskörper

Das Volumen des Rotationskörpers erhältst du jetzt, wenn du die beiden gerade berechneten Volumina addierst:

$V = V_K + V_Z = 30667{,}1\ \text{cm}^3\ +\ 6927{,}2\ \text{cm}^3 = 37594{,}3 \ \text{cm}^3.$