Teil B - lernen mit Serlo!

Aufgabe B3

Gegeben ist die Funktion $f_{1}$ mit der Gleichung $y = {0,75}^{x - 4} + 1$ $(x, y \in ℝ)$ und die Funktion $f_{2}$ mit der Gleichung $y = {0,75}^{x - 2} - 3$ $(x, y \in ℝ)$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

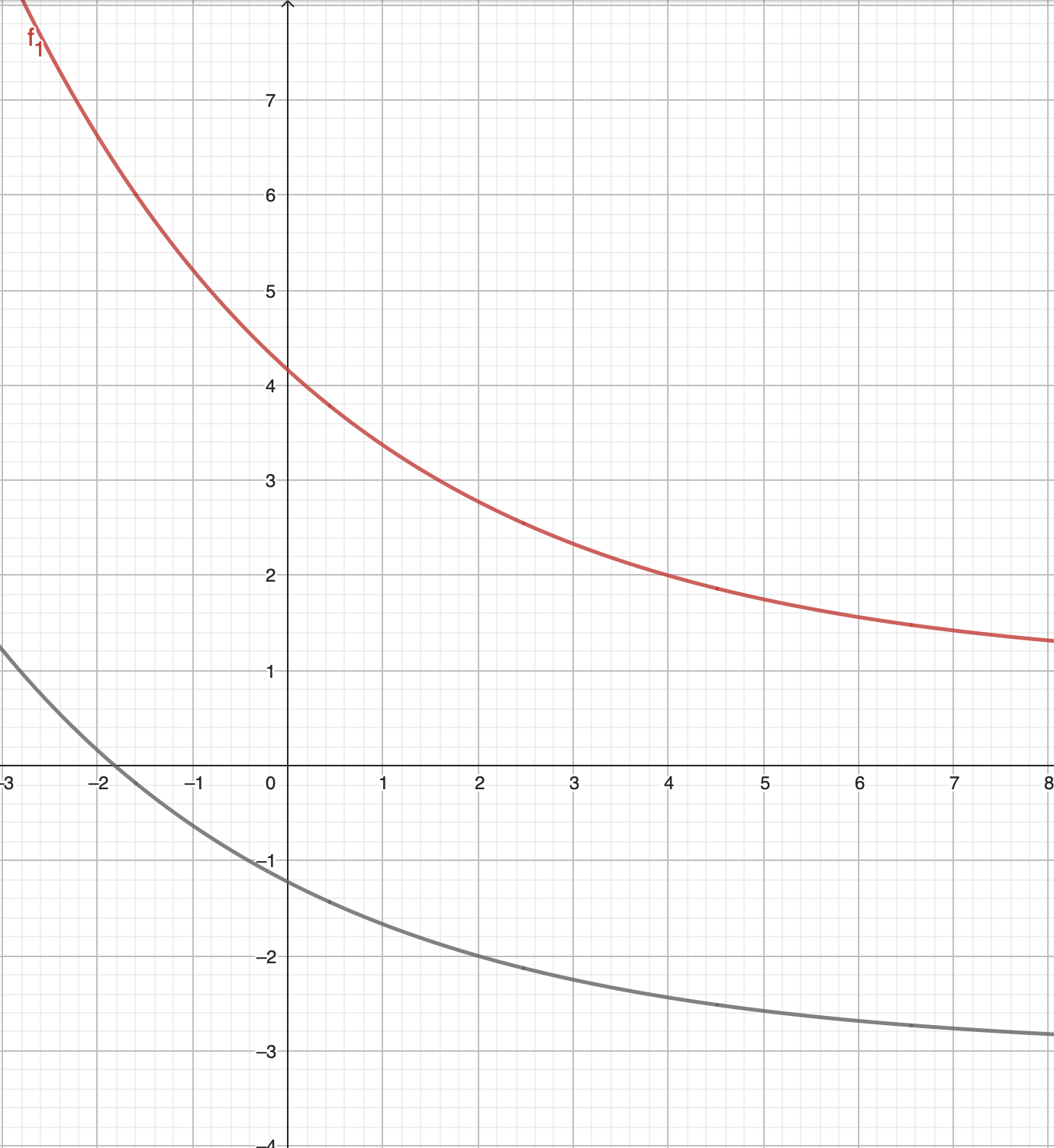
Geben Sie die Wertemenge von $f_{1}$ an und zeichnen Sie die Graphen zu $f_{1}$ und $f_{2}$ für
$x \in [- 3; 8]$ in ein Koordinatensystem. (4 P)
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 3 \leq x \leq 8; - 4 \leq y \leq 9$
Wertebereich von $f_{1}$
Dafür betrachten wir das Grenzwertverhalten:
$f_{1}$ geht für $x \to - \infty$ gegen unendlich
$x = 1$ ist die waagrechte Asymptote, deshalb geht $f_{1}$ für $x \to \infty$ gegen $1$
Weil $f_{1}$ monoton fällt, ergibt sich damit der Wertebereich $W =] 1; \infty [$
Wertetabelle für die einzelnen Funktionen
$f_{1} P u n k t e w e r t e$ :
$f_{2} P u n k t e w e r t e$
Mithilfe der erhaltenen Werte zeichnen wir die beiden Graphen
Zeichnung $f_{1}$ und $f_{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte das Grenzwertverhalten von $f_{1}$ und ermittle so die Wertemenge.
Erstelle eine Wertetabelle für die beiden Funktionen $f_{1}$ und $f_{2}$ .
Zeichne mithilfe der Wertetabelle die beiden Graphen $G_{f_{1}}$ und $G_{f_{2}}$ .
Der Graph der Funktion $f_{1}$ kann durch Parallelverschiebung mit dem Vektor $\vec{v} = (\begin{array}{c} x_{v} \\ y_{v} \end{array})$
auf den Graphen der Funktion $f_{2}$ abgebildet werden $(x_{v}, y_{v} \in ℝ)$ .
Geben Sie die Koordinaten des Vektors $\vec{v}$ an. (1 P)

Parallelverschiebung der Funktion $f_{1}$ auf $f_{2}$ mit $\vec{v}$
$\Rightarrow$ Vektoraddition mit Ortsvektoren und Verschiebungsvektor $\vec{v}$
${\vec{O P^{'}}}_{f_{1}} = {\vec{O P}}_{f_{2}} \oplus︎ (\begin{array}{c} x_{v} \\ y_{v} \end{array})$
$(\begin{array}{c} x^{'} \\ \underset{y^{'}}{\underset{⏟}{{0,75}^{(x^{'} - 2)} - 3}} \end{array}) = (\begin{array}{c} x \\ {0,75}^{(x - 4)} + 1 \end{array}) \oplus︎ (\begin{array}{c} x_{v} \\ y_{v} \end{array})$
Daraus ergeben sich diese zwei Gleichungen:
$x^{'} = x + x_{v}$
${0,75}^{(x^{'} - 2)} - 3 = {0,75}^{(x - 4)} + 1 + y_{v}$
$x^{'}$ in die zweite Gleichung einsetzen
${0,75}^{(x + x_{v} - 2)} - 3 = {0,75}^{(x - 4)} + 1 + y_{v}$
Für die Berechnung von $x_{v}$ vergleichen wir die $Exponenten$ :
$\to x + x_{v} - 2 = x - 4 | - x$
$\to x_{v} - 2 = - 4 | + 2$
$\Rightarrow x_{v} = - 2$
Für die Berechnung von $y_{v}$ vergleichen wir die $Konstanten$ der Gleichung:
$\Rightarrow - 3 = 1 + y_{v} | - 1$
$\to y_{v} = - 4$
$\Rightarrow \vec{v} = (\begin{array}{c} - 2 \\ - 4 \end{array})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Führe eine Parallelverschiebung mit dem Vektor $\vec{v} = (\begin{array}{c} x_{v} \\ y_{v} \end{array})$ durch.
Punkte $A_{n} (x | {0,75}^{x - 4} + 1)$ auf dem Graphen zu $f_{1}$ und Punkte $B_{n} (x | {0,75}^{x - 2} - 3)$ auf
dem Graphen zu $f_{2}$ haben dieselbe Abszisse $x$ . Sie sind zusammen mit Punkten $C_{n}$
Eckpunkte von Dreiecken $A_{n} B_{n} C_{n}$ .
Es gilt: $| A_{n} C_{n} | = 5 LE$ ; $∢ B_{n} A_{n} C_{n} = 60^{\circ}$ .
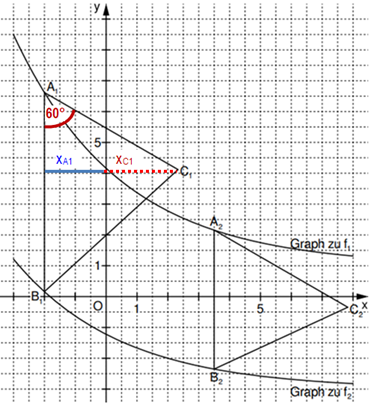
Zeichnen Sie das Dreieck $A_{1} B_{1} C_{1}$ für $x = - 2$ und das Dreieck $A_{2} B_{2} C_{2}$ für $x = 3,5$ in das Koordinatensystem zu Aufgabe a) ein.
Berechnen Sie sodann die x-Koordinate des Punktes $C_{1}$ . (4 P)
$△ A_{1} B_{1} C_{1}$ für $x = - 2$ bestimmen
Zunächst bestimmen wir die Koordinaten von $A_{1}$ und $B_{1}$ , indem wir $x = - 2$ in die allgemeine Form einsetzen:
$A_{1} (- 2 | {0,75}^{- 2 - 4} + 1) \Rightarrow A_{1} (- 2 | 6,619)$
$B_{1} (- 2 | {0,75}^{- 2 - 2} - 3) \Rightarrow B_{1} (2 | 0,16)$
$∢ B_{1} A_{1} C_{1} = 60 °$ an die Strecke $A_{1} B_{1}$ antragen und $5 LE$ zu $C_{1}$ abmessen
$△ A_{2} B_{2} C_{2}$ für $x = 3,5$ bestimmen
Zunächst bestimmen wir die Koordinaten von $A_{2}$ und $B_{2}$ , indem wir $x = 3,5$ in die allgemeine Form einsetzen:
$A_{1} (3,5 | {0,75}^{3,5 - 4} + 1) \Rightarrow A_{1} (3,5 | 2,155)$
$B_{1} (3,5 | {0,75}^{3,5 - 2} - 3) \Rightarrow B_{1} (3,5 | - 2,35)$
$∢ B_{2} A_{2} C_{2} = 60 °$ an die Strecke $A_{2} B_{2}$ antragen und $5 LE$ zu $C_{2}$ abmessen
Einzeichnen $△ A_{1} B_{1} C_{1}$ und $△ A_{2} B_{2} C_{2}$ mit berechneten Punktewerten und Winkel:
Berechnung der $x -$ Koordinate von Punkt $C_{1}$
$\sin (60 °)$ $=$ $\frac{G K}{H Y}$
$\sin (60 °)$ $=$ $\frac{x_{C_{1}} - x_{A_{1}}}{A_{1} C_{1}}$
$\sin (60 °)$ $=$ $\frac{x_{C_{1}} - (- 2)}{5}$ $\cdot 5$
$5 \cdot \sin (60 °)$ $=$ $x_{C_{1}} + 2$ $- 2$
$x_{C_{1}}$ $=$ $5 \cdot \sin (60 °) - 2$
$\approx$ $2,33 LE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $x = - 2$ und $x = 3,5$ in die allgemeine Form von $A_{n}$ und $B_{n}$ ein
Trage die Punkte in dein Koordinatensystem ein, füge den Winkel $∢ B_{n} A_{n} C_{n}$ . hinzu und miss $5 cm$ ab.
Verbinde nun die zusammengehörenden Punkte und du erhältst die gesuchten Dreiecke.
Teile das Dreieck $A_{1} B_{1} C_{1}$ so ein, dass du einen rechten Winkel erhältst. Berechne damit die x-Koordinate von $C_{1}$ mithilfe der Sinusformel indem du bekannte Werte nutzt.
Zeigen Sie rechnerisch, dass für die Länge der Strecken $A_{n} B_{n}$ in Abhängigkeit von
der Abszisse $x$ der Punkte $A_{n}$ gilt:
$| A_{n} B_{n} | (x) = (0,78 \cdot {0,75}^{x - 2} + 4) LE$ .
Berechnen Sie sodann den Flächeninhalt des Dreiecks $A_{1} B_{1} C_{1}$ . (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
Berechnung der Strecke $| A_{n} B_{n} |$
Uns fällt auf, dass die Strecke $A_{n} B_{n}$ (unabhängig vom eingesetzten x-Wert) immer senkrecht im Koordinatensystem steht.
Also berechnen wir die Länger der Strecke mit der $D i f f e r e n z$ der beiden y-Werte von $A_{n}$ und $B_{n}$ :
$| A_{n} B_{n} | (x) = [{0,75}^{x - 4} + 1 - ({0,75}^{x - 2} - 3)] L E$ $x \in ℝ$
$= {0,75}^{x - 4} + 1 - {0,75}^{x - 2} + 3$
$= {0,75}^{x - 4} - {0,75}^{x - 2} + 4$
$= {0,75}^{x - 2 - 2} - {0,75}^{x - 2} + 4$ $| {0,75}^{x - 2}$ ausklammern
$= {0,75}^{x - 2} \cdot ({0,75}^{- 2} - 1) + 4 |$ Klammer ausrechnen
$\approx {0,75}^{x - 2} \cdot (1,78 - 1) + 4$
$= {0,75}^{x - 2} \cdot (0,78) + 4$
$| A_{n} B_{n} | (x) = (0,78 \cdot {0,75}^{x - 2} + 4) LE$
Fläche $A_{△ A_{1} B_{1} C_{1}}$ berechnen mit der Flächenformel:
$A_{△ A_{1} B_{1} C_{1}} = \frac{1}{2} \cdot | A_{1} B_{1} | \cdot | A_{1} C_{1} | \cdot \sin ∢ B_{1} A_{1} C_{1}$
Wir berechnen zunächst die einzelnen Bestandteile:
Zur Berechnung von $| A_{1} B_{1} |$ nutzen wir die gerade berechnete Formel für $| A_{n} B_{n} |$ und setzen $x = - 2$ ein
$\begin{array}{l} | A_{1} B_{1} | = (0,78 \cdot {0,75}^{(- 2 - 2)} + 4) \\ = 0,78 \cdot {0,75}^{- 4} + 4 \end{array}$
$\begin{array}{l} = 0,78 \cdot \frac{1}{{0,75}^{4}} + 4 \\ = 0,78 \cdot \frac{1}{0,316} + 4 \\ = 6,47 LE \end{array}$ ;
$| A_{1} C_{1} | = 5 LE$
und mit $\sin ∢ B_{1} A_{1} C_{1} = \sin 60 ° ≙ 0,866$
$\Rightarrow A_{△ A_{1} B_{1} C_{1}} = \frac{1}{2} \cdot 6,47 \cdot 5 \cdot 0,866 \approx 14,01 FE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Vergleiche die Punkte $A_{1}$ und $B_{1}$ sowie $A_{2}$ und $B_{2}$ in deiner Zeichnung. Was fällt dir auf?
Berechne die Länge der Strecke über die Differenz der y-Koordinaten von $A_{n}$ und $B_{n}$ .
Nutze für die Berechnung des Flächeninhalts des Dreiecks $A_{1} B_{1} C_{1}$ die Flächenformel mit dem Sinus.
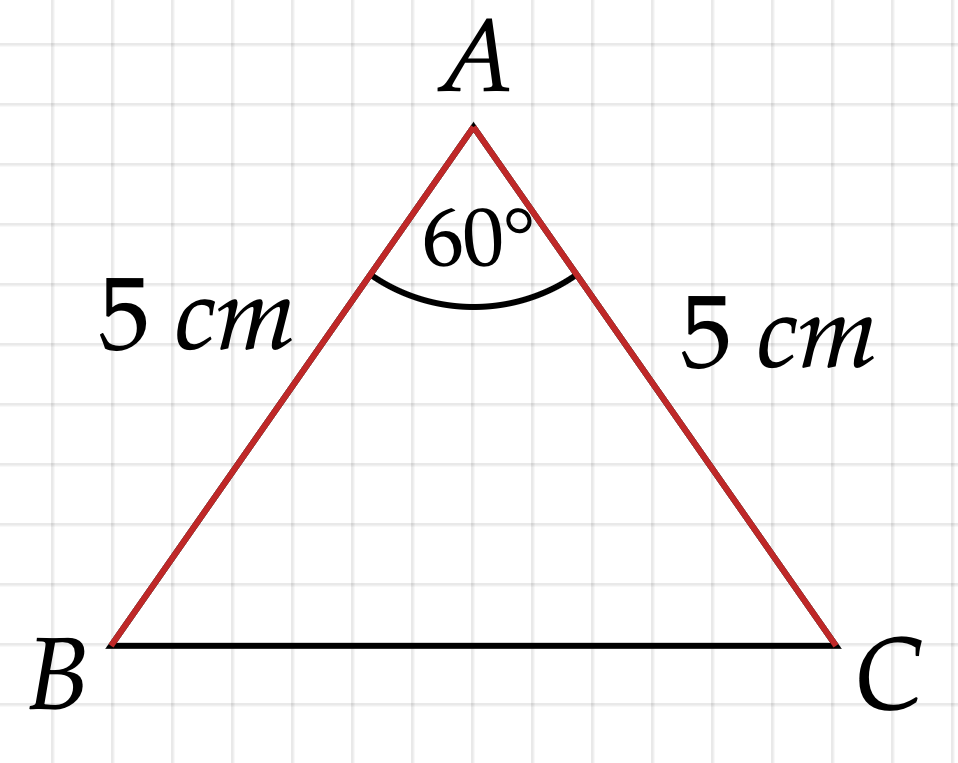
Das Dreieck $A_{3} B_{3} C_{3}$ ist gleichschenklig mit der Basis $B_{3} C_{3}$ .
Berechnen Sie die zugehörige x-Koordinate des Punktes $A_{3}$ . (2 P)
Das Dreieck $A_{3} B_{3} C_{3}$ ist gleichschenklig mit der Basis $B_{3} C_{3}$ .
Daraus folgt, dass Die Seiten $| A_{3} B_{3} |$ und $| A_{3} C_{3} |$ die gleiche Länge besitzen.
Da $| A_{3} C_{3} |$ immer 5 LE besitzt, muss also gelten: $| A_{3} B_{3} | = 5$ LE
Setze 5 LE mit der allgemeinen Formel für $| A_{n} B_{n} |$ gleich:
$| A_{n} B_{n} | (x)$ $=$ $5$
$0,78 \cdot {0,75}^{x - 2} + 4$ $=$ $5$ $- 4$
$0,78 \cdot {0,75}^{x - 2}$ $=$ $1$ $: 0,78$
${0,75}^{x - 2}$ $\approx$ $1,28$ $\log_{0,75}$
$x - 2$ $=$ $\log_{0,75} (1,28)$ $+ 2$
$x$ $\approx$ $- 0,86 + 2$
$x$ $=$ $1,14$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege dir, welche Auswirkung ein gleichschenkliges Dreieck auf die Seitenlängen eines Dreiecks hat.
Schließe nun auf die Seitenlänge der unbekannten Seite $| A_{3} B_{3} |$ .
Berechne $x_{A_{3}}$ mit $| A_{n} B_{n} | (x)$ und dem Wert von $| A_{3} B_{3} | (x) = 5 LE$ .
Begründen Sie, weshalb das Dreieck $A_{3} B_{3} C_{3}$ gleichseitig ist. (1,5 P)
Bei einem Gleichschenkligen Dreieck haben die beiden Basiswinkel dasselbe Winkelmaß. Es gilt also:
$∢ C B A = ∢ A C B$
Wir kennen bereits einen Winkel im Dreieck: $∢ B A C = 60^{\circ}$
Durch die Innenwinkelsumme eines Dreiecks folgt deshalb:
$\begin{array}{l} ∢ B A C + ∢ C B A + ∢ A C B = 180 ° \\ 60 ° + 2 \cdot ∢ C B A = 180 ° \\ 2 \cdot ∢ C B A = 120 ° \\ ∢ C B A = 60 ° \end{array}$
Skizze gleichschenkliges Dreieck
Also gilt: $∢ B A C = ∢ C B A = ∢ A C B = 60 °$ und somit müssen alle Seiten die gleiche Länge besitzen und des handelt sich um ein gleichseitiges Dreieck.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege dir, welche Konsequenzen ein gleichschenkliges Dreieck für die Winkelmaße in dem Dreieck hat.
Berechne alle Winkel des Dreiecks $A_{3} B_{3} C_{3}$ . Nutze hierfür bekannte Maße und die Innenwinkelsumme eines Dreiecks
Folgere daraus, dass es sich bei $A_{3} B_{3} C_{3}$ um ein gleichseitiges Dreieck handeln muss.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$\sin (60 °)$	$=$	$\frac{G K}{H Y}$
$\sin (60 °)$	$=$	$\frac{x_{C_{1}} - x_{A_{1}}}{A_{1} C_{1}}$
$\sin (60 °)$	$=$	$\frac{x_{C_{1}} - (- 2)}{5}$	$\cdot 5$
$5 \cdot \sin (60 °)$	$=$	$x_{C_{1}} + 2$	$- 2$
$x_{C_{1}}$	$=$	$5 \cdot \sin (60 °) - 2$
	$\approx$	$2,33 LE$

$\| A_{n} B_{n} \| (x)$	$=$	$5$
$0,78 \cdot {0,75}^{x - 2} + 4$	$=$	$5$	$- 4$
$0,78 \cdot {0,75}^{x - 2}$	$=$	$1$	$: 0,78$
${0,75}^{x - 2}$	$\approx$	$1,28$	$\log_{0,75}$
$x - 2$	$=$	$\log_{0,75} (1,28)$	$+ 2$
$x$	$\approx$	$- 0,86 + 2$
$x$	$=$	$1,14$

Aufgabe B3

Wertebereich von f1

Wertetabelle für die einzelnen Funktionen

Mithilfe der erhaltenen Werte zeichnen wir die beiden Graphen

Hast du eine Frage oder Feedback?

Parallelverschiebung der Funktion f1 auf f2 mit v→

x′ in die zweite Gleichung einsetzen

Hast du eine Frage oder Feedback?

△A1B1C1 für x=−2 bestimmen

△A2B2C2 für x=3,5 bestimmen

Einzeichnen △A1B1C1 und △A2B2C2 mit berechneten Punktewerten und Winkel:

Berechnung der x−Koordinate von Punkt C1

Hast du eine Frage oder Feedback?

Berechnung der Strecke |AnBn|

Fläche A△A1B1C1 berechnen mit der Flächenformel:

Hast du eine Frage oder Feedback?

Setze 5 LE mit der allgemeinen Formel für |AnBn| gleich:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wertebereich von $f_{1}$

Parallelverschiebung der Funktion $f_{1}$ auf $f_{2}$ mit $\vec{v}$

$x^{'}$ in die zweite Gleichung einsetzen

$△ A_{1} B_{1} C_{1}$ für $x = - 2$ bestimmen

$△ A_{2} B_{2} C_{2}$ für $x = 3,5$ bestimmen

Einzeichnen $△ A_{1} B_{1} C_{1}$ und $△ A_{2} B_{2} C_{2}$ mit berechneten Punktewerten und Winkel:

Berechnung der $x -$ Koordinate von Punkt $C_{1}$

Berechnung der Strecke $| A_{n} B_{n} |$

Fläche $A_{△ A_{1} B_{1} C_{1}}$ berechnen mit der Flächenformel:

Setze 5 LE mit der allgemeinen Formel für $| A_{n} B_{n} |$ gleich: