Nachtermin Teil B - lernen mit Serlo!

Aufgabe B3

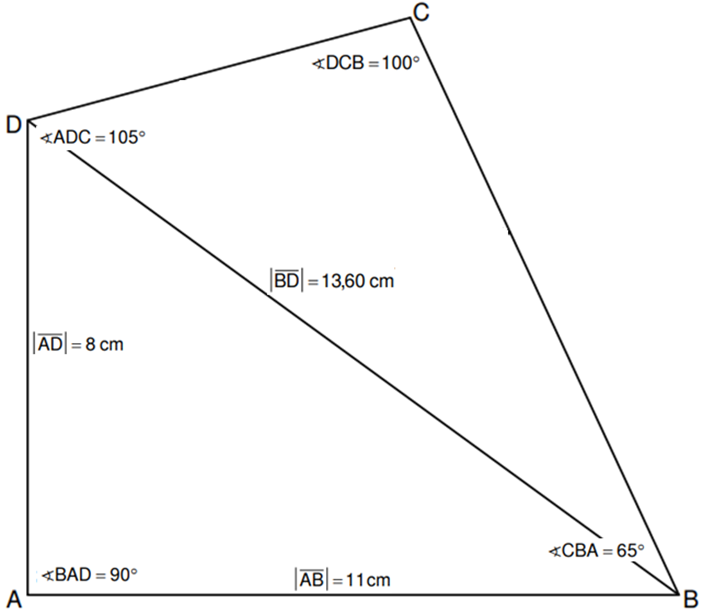
Die nebenstehende Skizze zeigt das Viereck $A B C D$ .

Es gilt: $\vert\overline{AB}\vert=11\;\text{cm}$ ; $\vert\overline{AD}\vert=8\;\text{cm}$ ;

$\sphericalangle CBA=65^\circ$ ; $\sphericalangle ADC=105^\circ$ ; $\sphericalangle BAD=90^\circ$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie das Viereck $A B C D$ und die Strecke $\overline{BD}$ .
Berechnen Sie sodann das Maß des Winkels $D C B$ und die Länge der Strecke $\overline{BD}$ . (3,5 P)
$[$ Teilergebnisse: $\sphericalangle DCB=100^\circ; \vert\overline{BD}\vert=13{,}60\;\text{cm}]$

geg.: $|\overline {AB}|= 11\:cm;\:|\overline {AD}|= 8\:cm; \: \sphericalangle CBA=65°; \: \sphericalangle ADC=105°; \: \sphericalangle BAD=90°$
ges.: Winkel $D C B$ und Länge der Strecke $|\overline {BD}|$
Ansatz und Rechnung:
Grundwissen: Pythagoras, allgemeine Vierecke, Sinussatz, Kosinussatz, Kreisbogen, Prozentrechnung.
1. Zeichnen des Vierecks ABCD und der Strecke $|\overline {BD}|$
Viereck ABCD mit Diagonale $|\overline {BD}|$
2. Berechnung von $|\overline {BD}|$ mithilfe Pythagoras:
$B D^{2} = A B^{2} + A D^{2}$
$\Rightarrow |\overline {BD}|=\sqrt {AB^2+AD^2}=\sqrt {11^2+8^2 }=\sqrt{121+64}=\sqrt {185}\: cm$
$\bold {\Rightarrow |\overline {BD}|=13{,}60 \:cm}$
3. Berechnung von Winkel $D C B$
$\sphericalangle DCB=360°-\sphericalangle CBA-\sphericalangle ADC -\sphericalangle BAD$
$⇒ \sphericalangle DCB=360°-65°-105° -90°$
$\bold {\Rightarrow \sphericalangle DCB=100°}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeichnung des Vierecks $A B C D$ und der Strecke $\overline{BD}$ ; Berechnung des Winkels $D C B$ und der Länge der Strecke $\overline{BD}$
Berechnen Sie die Längen der Strecken $\overline{DC}$ und $\overline{BC}$ . (4 P)
$[$ Zwischenergebnis: $\sphericalangle CBD=28{,}97^\circ$ ; Teilergebnis $\vert\overline{BC}\vert=10{,}74\;\text{cm}]$

geg.: $|\overline {AB}|= 11\:cm;\:|\overline {AD}|= 8\:cm; \: \sphericalangle CBA=65°; \: \sphericalangle ADC=105°;$
$\: \sphericalangle BAD=90°; \: \sphericalangle DCB=100°;\:\overline {BD}|= 13{,}60\:cm$
ges.: Längen der Strecken $\overline {DC}$ und $\overline {BC}$
Ansatz und Rechnung:
1. Berechnung der Strecke $\overline {DC}$ mit Sinussatz und Tangens:
Im Dreieck $B C D$ sind bisher nur die Strecke $\overline{BD}$ und der Winkel $\sphericalangle BCD$ bekannt.
Daher muss zunächst eine dritte Größe berechnet werden:
berechne den Winkel $\sphericalangle DBA$ im rechtwinkligen Dreieck $A B D$ und mit dem bekannten Winkel $\sphericalangle ADC$ den Winkel $\sphericalangle BDC$ .
$\sphericalangle DBA$ wird berechnet mit $\tan \sphericalangle DBA =\frac{8}{11}\quad \Rightarrow \quad \sphericalangle DBA=36{,}06°$
Somit ist $\sphericalangle CBD=\sphericalangle CBA-\sphericalangle DBA =65°-36{,}03° \Rightarrow \quad \sphericalangle CBD=28{,}97°$
Sinussatz $\displaystyle\frac {\red a}{\sin \red α }=\frac {\blue b}{\sin \blue β }=\frac {\green c}{\sin\green γ}$ angewandt auf Dreieck $B C D$ ergibt:
$\displaystyle\frac {|\overline {DC}|}{\sin \sphericalangle CBD }=\frac {|\overline {BD}|}{sin \sphericalangle DCB}$ $\displaystyle\quad \Rightarrow \frac {|\overline {DC}|}{\sin28{,}97^\circ }=\frac {13{,}60\text{ cm}}{\sin 100^\circ}$
Aufgelöst nach $\overline {DC}$ ergibt das:
$\displaystyle\bold {|\overline {DC}|} =\frac {13{,}60\: cm \cdot \sin(28{,}97^\circ)}{\sin(100^\circ)}=\frac {13{,}60 \cdot 0{,}48435}{0{,}98481}=6{,}6887 \bold {\approx 6{,}69\text{ cm}}$
2. Berechnung der Strecke $\overline {BC}$ mit Kosinussatz:
Zuerst wird der Winkel $\sphericalangle BDC$ mit Hilfe der Winkelsumme im Dreieck bestimmt:
$\sphericalangle BDC=180^\circ-100^\circ-28{,}97^\circ=51{,}03^\circ$
Der Kosinussatz $\red {a^2=b^2+c^2-2\cdot b \cdot c\cdot \cos\sphericalangle BDC }$ angewandt auf die Strecke $\overline {BC}$ ergibt:
$|\overline {BC}^2|= |\overline {BD}^2|+|\overline {DC}^2|-2\cdot\overline {BD}\cdot \overline {DC} \cdot \cos\sphericalangle BDC$
$\Rightarrow |\overline {BC}|= \sqrt {|\overline {BD}^2|+|\overline {DC}^2|-2\cdot\overline {BD}\cdot \overline {DC} \cdot \cos\sphericalangle BDC}$
$\Rightarrow |\overline {BC}|= \sqrt {13{,}6^2+6{,}69^2-2\cdot 13{,}60 \cdot 6{,}69 \cdot \cos(51{,}03°)}$
$\Rightarrow |\overline {BC}|= \sqrt {184{,}96+44{,}76-181{,}97 \cdot 0{,}62891}$
$\Rightarrow \bold {|\overline {BC}|}= \sqrt {184{,}96+44{,}76-114{,}44}= \sqrt {115{,}28}=10{,}7368 \approx \bold {10{,}74 \: cm}$
Hinweis: Diese Berechnung kannst du auch mit den bekannten Größen $|\overline{BD}|$ , $\sphericalangle DCB$ und dem Winkel $\sphericalangle BDC$ , den du wie in der Rechnung oben bestimmst und dem Sinussatz durchführen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne zunächst den Winkel $\sphericalangle BDA$ , um den Winkel $\sphericalangle CDB$ zu bestimmen.
Verwende dann Sinussatz und Kosinussatz.
Bestimmen Sie den Flächeninhalt $A_{ABCD}$ des Vierecks $A B C D$ . (2 P)
$[$ Ergebnis: $A_{ABCD}=79{,}37\;\text{cm}^2]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
geg.: Wertangaben und Rechenergebnisse aus Aufgabe $B 3. a$ und $B 3. b$
ges.: Gesamtfläche $A_{ABCD}$ bestehend aus $\triangle ABD$ und $\triangle BCD$
Ansatz und Rechnung:
1. Berechnung der Fläche des rechtwinkligen $\triangle ABD$ :
$A_{\triangle ABD}=\frac{1}{2}\cdot g \cdot h$ mit $g= |\overline {AB}|=11\: cm$ und $h= |\overline {AD}|=8\: cm$
$\bold {A_{\triangle ABD}}=\frac{1}{2}\cdot 11\: cm \cdot 8 \:cm=\bold {44\:cm^2}$
2. Berechnung der Fläche des allgemeinen $\triangle BCD$ mithilfe des Sinussatzes:
Der Sinussatz mit zwei Seitenlängen und dem eingeschlossenen Winkelmaß lautet:
$\blue {\bold {A=\frac{1}{2}\cdot a \cdot b \cdot sinγ}}$
mit $a=|\overline {BD}|= 13{,}60\:cm;\quad b=|\overline {BC}|= 10{,}74\:cm; \quad \sin\measuredangle CBD=28{,}97°$
$\Rightarrow \bold { A_{\triangle BCD}}=\:\frac{1}{2}\cdot 13{,}6 \cdot 10{,}74 \cdot \sin(28{,}97°)\quad =73{,}032\cdot0{,}48435\quad =\bold {35{,}37\: cm^2}$
3. Berechnung der Gesamtfläche des Vierecks $A B C D$ :
$\bold {A_{\square ABCD}}=A_{\triangle ABD}+A_{\triangle BCD}=44+35{,}37=\bold {79{,}37\: cm^3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimmung des Flächeninhalts von Viereck $A B C D$ bestehend aus dem rechwinkligen Dreieck $A B D$ und dem allgemeinen Dreieck $B C D$
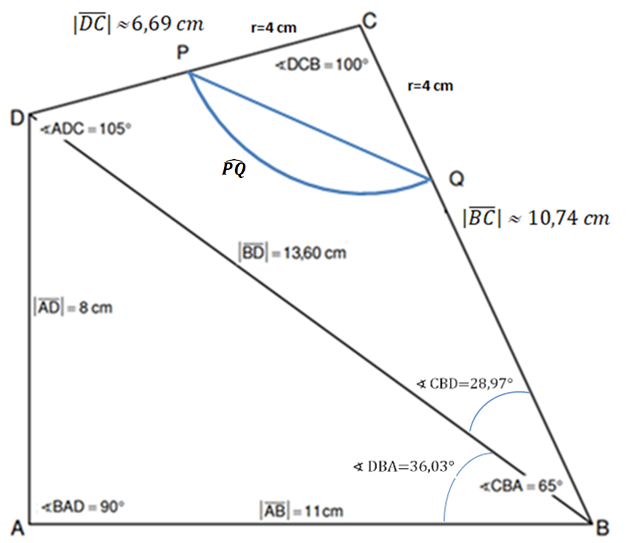
Der Kreis mit dem Mittelpunkt $C$ und dem Radius $r=4\;\text{cm}$ schneidet die Strecke $\overline{DC}$ im Punkt $P$ und die Strecke $\overline{BC}$ im Punkt $Q$ .
Ergänzen Sie in der Zeichnung zu Aufgabe a) den Kreisbogen $\overset\frown{PQ}$ mit dem Mittelpunkt $C$ und die Strecke $\overline{PQ}$ . (1 P)

1. Einzeichnen des Kreisbogens $\overset\frown{PQ}$ mit Radius $r=4\: cm$ um Mittelpunkt $C$ .
2. Kreisbogen schneidet die Strecke $\overline {DC}$ in Punkt $P$ und die Strecke $\overline {BC}$ in $Q$
Viereck ABCD mit Strecke $\overline {PQ}$ und Kreisbogen $\overset\frown{PQ}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Geometrische Zeichnung anfertigen
Der Kreisbogen $\overset\frown{PQ}$ und die Strecke $\overline{PQ}$ begrenzen eine Figur.
Berechnen Sie den Umfang dieser Figur. (2,5 P)

geg.: Kreismittelpunkt ist Eckpunkt $C$ des Vierecks $A B C D$ ; Kreisradius ist $r=4\:cm ≙\overline {CP}≙\overline {CQ}$ ; Öffnungswinkel des Kreisbogensektors ist $∢ P C Q = 100 °$
ges.: Kreisbogenlänge $|\overset\frown{PQ}|$ und Strecke $|\overline {PQ}|$ (=Kreissehne)
Ansatz und Rechnung:
1. Berechnung der Kreisbogenlänge mithilfe der Kreisbogenformel:
$\bold {{b=\dfrac{\alpha }{360^\circ}\cdot 2\cdot π\cdot r}}\qquad$ mit $\alpha=100^\circ$ ; $\:π =3{,}14$ ; $\:r=4\:cm$
$\Rightarrow \bold {\overset\frown{PQ}}=\dfrac{100°}{360°}\cdot 2\cdot 3{,}14\cdot 4\:cm=\bold {6{,}98\text{ cm}}$
2. Berechnung der Strecke $|\overline {PQ}|$ mithilfe des Kosinussatzes:
$\bold { {a^2=b^2+c^2-2 \cdot b\cdot c \cdot \cos α}}$
mit $a= |\overline {PQ}|$ ; $\quad b=r=|\overline {CP}|= 4\: cm$ ; $\quad c=r=|\overline {CQ}|= 4\: cm$ ; $\quad \alpha=100$
$\Rightarrow \bold {|\overline {PQ}|^2}=4^2+4^2-2⋅4⋅4⋅\cos⁡(100°)$
$\Rightarrow \bold {|\overline {PQ}|^2}=16+16 \bold {−}32 ⋅ (\bold{−} 0{,}173648)=32 \bold {+} 5{,}5567= 37{,}5567$
$\Rightarrow \bold {|\overline {PQ}|}=\sqrt {37{,}5567}=6{,}1283 \approx \bold {6{,}13 \: cm}$
3. Berechnung des Umfangs der Figur (bestehend aus Kreisbogen $\overset\frown{PQ}$ und Sehne $|\overline {PQ}|$ :
$\bold {U_{Figur}}=|\overset\frown{PQ}|+|\overline {PQ}|=6{,}98\: cm+6{,}13\: cm=\bold {13{,}11\: cm}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Länge des Kreisbogens $\overset\frown{PQ}$ mit Winkel und Radius und die der Strecke $\overline {PQ}$ mit dem Kosinussatz.
Berechnen Sie den prozentualen Anteil des Flächeninhalts der Figur aus e) am
Flächeninhalt des Vierecks $A B C D$ . (3 P)

Grundwissen: Kreissektorformel, Sinussatz für Dreiecksfläche, Prozentrechnung
geg.: Öffnungswinkel des Kreissektors ist $∢ P C Q = 100 °$ ; $\quad r=4\:cm$ ;
Kreisbogenlänge $|\overset\frown{PQ}|=6{,}98\: cm$ und Strecke $|\overline {PQ}|=6{,}13\:cm$ (Kreissehne)
ges.: $A_{\text{Figur}}$ und %-Anteil von $A_{\text{Figur}}$ an $A_{ABCD}$
Ansatz und Rechnung:
1. Berechnung der Fläche des Kreissektors $\bold {∢PCQ}$ mithilfe der Kreissektorformel:
Kreissektor $∢ P C Q$ Teilfläche eines Kreises, die vom Kreisbogen $|\overset\frown{PQ}|$ und den zwei Kreisradien $r$ begrenzt wird:
$\bold { {A_{Kreissektor∢α}=\frac{α}{360°}\cdot π\cdot r^2}}\quad$ mit $r=4\:cm$ und $\alpha =100°$
$\bold {A_{Kreissektor∢α}}=\frac{100°}{360°}\cdot 3{,}14\cdot 4^2=\bold {13{,}95\:cm^2}$
2. Berechnung der Dreiecksfläche von $\triangle PCQ$ mithilfe Sinussatz:
Der Sinussatz mit zwei Seitenlängen und dem eingeschlossenen Winkelmaß $\alpha$ lautet:
$A=\frac{1}{2}\cdot a \cdot b \cdot \sin\alpha \quad$ mit $a= b=r=4\: cm$ ; $\quad \alpha$ =100°
$\Rightarrow A_{\triangle PCQ}=\frac{1}{2}\cdot 4 \cdot 4 \cdot \sin(100°)$
$\Rightarrow \bold {A_{\triangle PCQ}}=\frac{1}{2}\cdot 4 \cdot 4 \cdot 0{,}98481=\bold {7{,}87\:cm^2}$
3. Berechnung der Figur (=Kreissegment) durch Subtraktion der Flächen:
Kreissektor $∢ P C Q$ minus Dreiecksfläche von $\triangle PCQ$ :
$\bold {A_{Figur}=A_{Kreissektor ∢\alpha}-A_{\triangle PCQ}}=13{,}95-7{,}87=6{,}08\:cm^2$
4. Berechnung des Prozentanteils der Figur (=Kreissegment $P Q$ ) an $A_{ABCD}=79{,}37\: cm2$ (gem. Aufgabe B 3.c)
$\displaystyle\frac{A_{Figur}}{A_{ABCD}}=\frac{6{,}08\:cm^2}{79{,}37\:cm^2}=0{,}0766$
$\Rightarrow$ Der $% -$ Anteil der Figur am Flächeninhalt des Vierecks $A B C D$ beträgt $\bold 7{,}66 \:\%$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimmung der Figurfläche (gebildet aus dem Kreisbogen $\overset\frown{PQ}\\$ und der Strecke $\overline {PQ}$ ); Bestimmung des %-Anteils der Figurfläche an Fläche des Vierecks $A B C D$

Aufgabe B3

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?