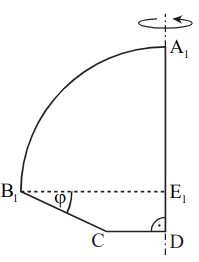
Gegeben sind die Trapeze mit den parallelen Seiten und . Die Winkel haben das Maß mit .
Kreise mit den Mittelpunkten haben die Radien und schneiden die Halbgeraden in den Punkten .
Die Figuren werden von den Kreisbögen sowie den Strecken , und begrenzt.
Es gilt: ; ; . Die Skizze zeigt die Figur für .
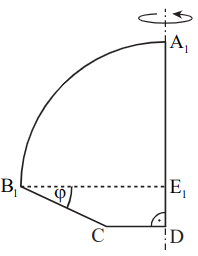
Zeigen Sie, dass für die Länge der Strecken in Abhängigkeit von gilt:
Die Figuren rotieren um die Geraden . Bestandteile der entstehenden Rotationskörper sind Halbkugeln. Bei dem Körper, der durch Rotation der Figur entsteht, hat die Halbkugel ein Volumen von .
Bestimmen Sie rechnerisch den Radius sowie das zugehörige Maß für .
Runden Sie auf zwei Stellen nach dem Komma.