Teil B, Gruppe 1 - lernen mit Serlo!

Die Abbildung zeigt ein Werkstück. Die Vorder- und Rückseite sind deckungsgleiche gleichschenklige Dreiecke.

Berechne den Oberflächeninhalt des Werkstücks.

Video bis 8:36.
Außerdem musst du wissen, wie man die Fläche eines Rechtecks berechnet.
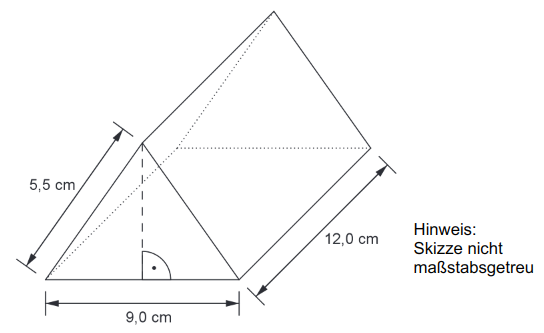
Die Gesamtoberfläche besteht aus dem vorderen und hinteren Dreieck, den beiden seitlichen Rechtecken und dem unteren Rechteck.
$\displaystyle O_{gesamt}=2\cdot A_{Dreieck}+2\cdot A_{Seitenrechteck}+A_{unteresRechteck}$
Der Flächeninhalt der Dreiecke berechnet sich wie folgt:
$\displaystyle A_{Dreieck}=\frac{g\cdot h}2$
Die Grundlinie kann man ablesen:
$\displaystyle g=9\,cm$
Die Höhe $h$ des Dreiecks muss man erst noch berechnen. Dies kannst du mit Hilfe des Satz von Pythagoras tun:
Die Summe der quadrierten Katheten ist gleich dem Quadrat der Hypotenuse.
$(4{,}5cm)^2+h^2=(5{,}5cm)^2$
$\def\arraystretch{1.25} \begin{array}{l}20{,}25cm^2+h^2=30{,}25cm^2\\h^2=30{,}25cm^2-20{,}25cm^2=10cm^2\\h\approx3{,}16cm\end{array}$
Damit beträgt der Flächeninhalt des Dreiecks:
$\displaystyle A_{Dreieck}=\frac{g\cdot h}2=\frac{9\;cm\cdot3{,}16\;cm}2=14{,}22\;cm^2$
Der Flächeninhalt eines seitlichen Rechtecks berechnet sich wie folgt:
$\displaystyle A_{Seitenrechteck}=a\cdot b=5{,}5\;cm\;\cdot12\;cm=66\;cm^2$
Die Fläche des unteren Rechtecks berechnest du wie folgt:
$\displaystyle A_{unteresRechteck}=b\cdot c=12\;cm\;\cdot9\;cm=108\;cm^2$
Nun setzt man alle gefundenen Werte in die erste Formel ein :
$\displaystyle \def\arraystretch{1.25} \begin{array}{l}O_{gesamt}&=2\cdot A_{Dreieck}+2\cdot A_{Seitenrechteck}+A_{unteresRechteck}\\&=2\cdot14{,}22\;cm^2+2\cdot66\;cm^2+108\;cm^2\\&=268{,}44\;cm^2\end{array}$
Der Oberflächeninhalt beträgt also $268{,}44\;cm^2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Ermittle das Volumen des Werkstücks.
cm³

Video ab 8:37.
Das Werkstück ist ein regelmäßiges Prisma mit dreieckiger Grundfläche.
$\displaystyle V=G\cdot h$
Die Grundfläche ist die Fläche des in Teilaufgabe a) berechneten Dreiecks. Also $G=14{,}22\;cm^2$ . Die Höhe $h$ beträgt $12\,cm$ . Das Volumen berechnet sich also wie folgt:
$\displaystyle V=14{,}22\;cm^2\cdot12\;cm=170{,}64\;cm^3$
Das Volumen beträgt $170{,}64cm^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?