Teil B, Gruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Für den Unterricht im Fach Soziales werden gelbe, rote und blaue Schürzen bestellt. Insgesamt sind es 83 Schürzen. Von den gelben werden dreimal so viele bestellt wie von den roten. Es werden 20 blaue Schürzen mehr bestellt als gelbe.
Wie viele Schürzen werden von jeder Farbe bestellt?
Stelle deinen Lösungsweg nachvollziehbar dar.
- 2
Die Abbildung zeigt ein Werkstück. Die Vorder- und Rückseite sind deckungsgleiche gleichschenklige Dreiecke.
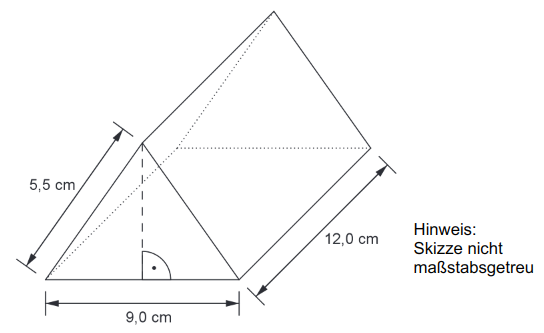
Berechne den Oberflächeninhalt des Werkstücks.
Ermittle das Volumen des Werkstücks.
cm³
- 3
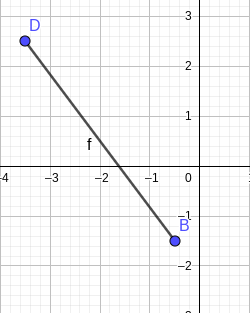
Zeichne in ein Koordinatensystem (Einheit 1 cm) die Punkte B (-0,5 |-1,5) und D(-3,5 |2,5) ein und verbinde sie zur Strecke [BD]. Hinweis zum Platzbedarf: x-Achse von -7 bis 3, y-Achse von -3 bis 4.
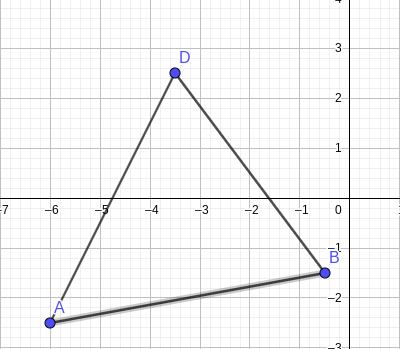
Verbinde die Punkte B und D mit dem Punkt A(-6 |-2,5) zu einem Dreieck. Gib an, welches besondere Dreieck dadurch entsteht.
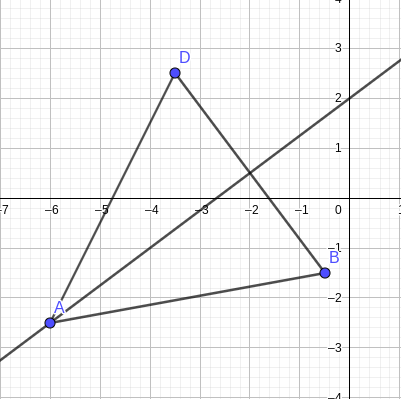
Zeichne die Senkrechte zu [BD] durch den Punkt A.
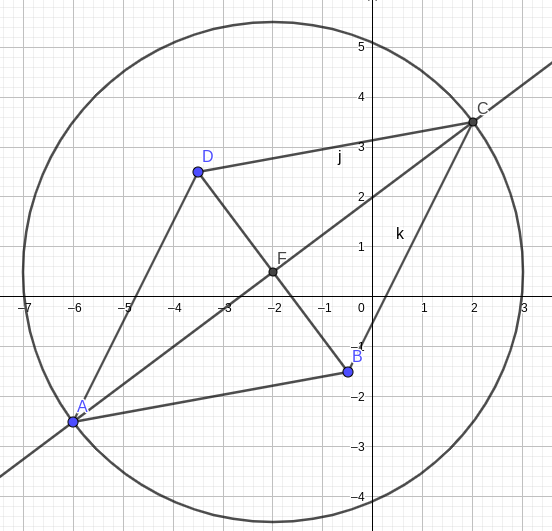
Lege den Punkt C so fest, dass die Raute ABCD entsteht, und beschrifte die Eckpunkte der Raute.
- 4
Die Tabelle zeigt, wie viel Gemüse jede Person in Deutschland durchschnittlich in einem Jahr isst.
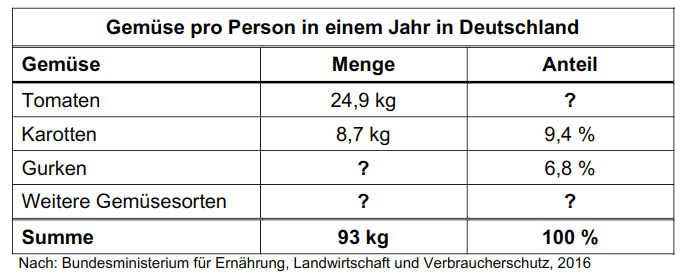
Berechne, wie viele Kilogramm Gurken eine Person durchschnittlich in einem Jahr isst.
Ermittle den prozentualen Anteil der Tomaten am verzehrten Gemüse.
Berechne, wie viele Kilogramm Gemüse eine vierköpfige Familie im Monat durchschnittlich isst.
kgDer durchschnittliche Verzehr von Gemüse pro Person in Deutschland ist um 2,6 % höher als der in Bayern. Ermittle, wie viele Kilogramm Gemüse jede Person in Bayern durchschnittlich pro Jahr isst.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?