🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

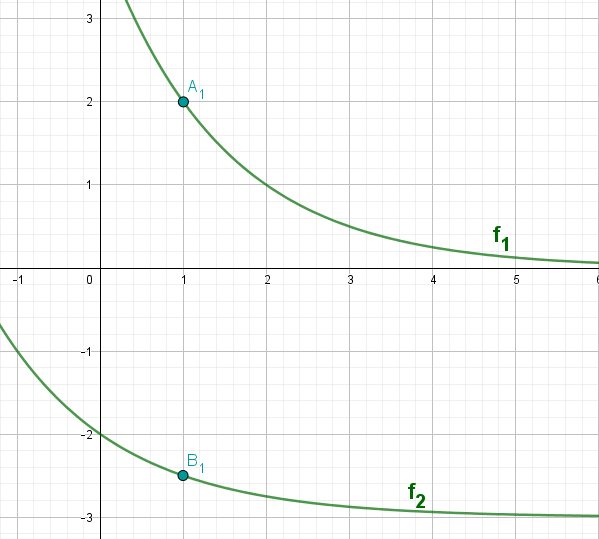
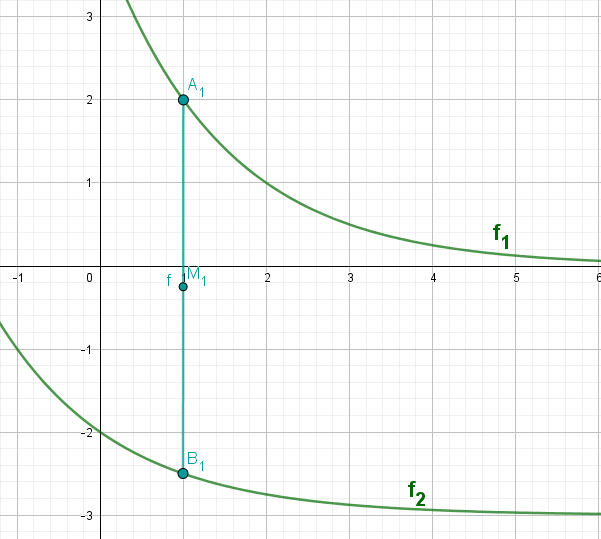
Gegeben sind die Funktionen f1f_1 mit der Gleichung y=4⋅0,5xy=4\cdot 0{,}5^x und f2f_2 mit der Gleichung y=4⋅0,5x+2−3   (G=R×R)y=4\cdot 0{,}5^{x+2}-3~~~(\mathbb{G}=\mathbb{R}\times\mathbb{R}). Punkte An(x∣4⋅0,5x)A_n(x|4\cdot 0{,}5^x) auf dem Graphen zu f1f_1 und Punkte Bn(x∣4⋅0,5x+2−3)B_n(x|4\cdot 0{,}5^{x+2}-3) auf dem Graphen zu f2f_2 haben dieselbe Abszisse xx. Die Strecken [AnBn][A_nB_n] sind für x∈Rx\in\mathbb{R} die Basen von gleichschenkligen Dreiecken AnBnCnA_nB_nC_n.

Für die Höhen [MnCn][M_nC_n] der Dreiecke AnBnCnA_nB_nC_n gilt: MnCn‾=3 LE\overline{M_nC_n}=3~\text{LE}

Bild

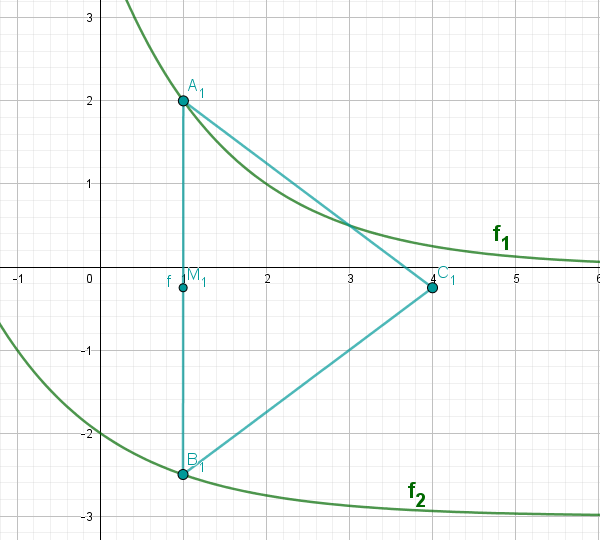
  1. Zeichnen Sie das Dreieck A1B1C1A_1B_1C_1 für x=1x=1 in das Koordinatensystem ein.

  2. Zeigen Sie durch Rechnung, dass für die Länge der Strecken [AnBn][A_nB_n] in Abhängigkeit von der Abszisse xx der Punkte AnA_n gilt: AnBn‾(x)=(3⋅0,5x+3) LE\overline{A_nB_n}(x)=(3\cdot 0{,}5^x+3)~\text{LE}

  3. Das Dreieck A2B2C2A_2B_2C_2 hat einen Flächeninhalt von 15 FE15~\text{FE}.

    Berechnen Sie den zugehörigen Wert für xx.