Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
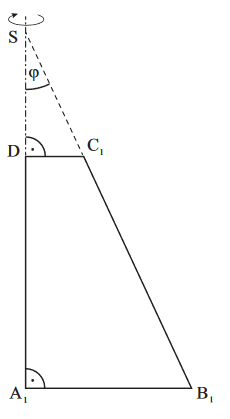
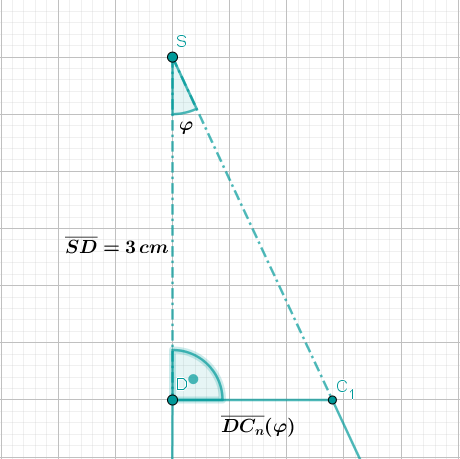
Trapeze mit den parallelen Seiten und rotieren um die Gerade .
Es gilt:
; ; ; .
Die Winkel haben das Maß mit .
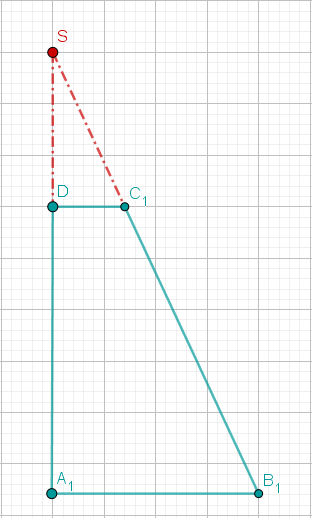
Die Zeichnung zeigt das Trapez für .
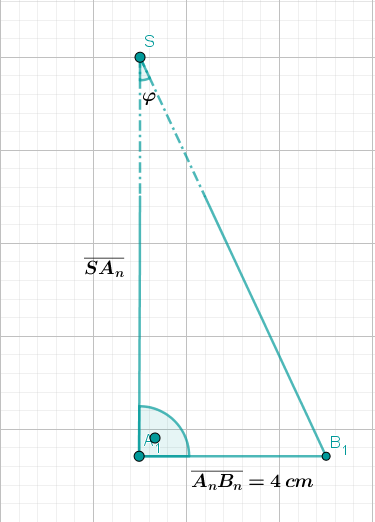
Zeichnen Sie in die Zeichnung zu das Trapez für ein.
(1 Punkt)
Zeigen Sie durch Rechnung, dass für die Längen der Strecken und in Abhängigkeit von gilt: und .
(2 Punkte)
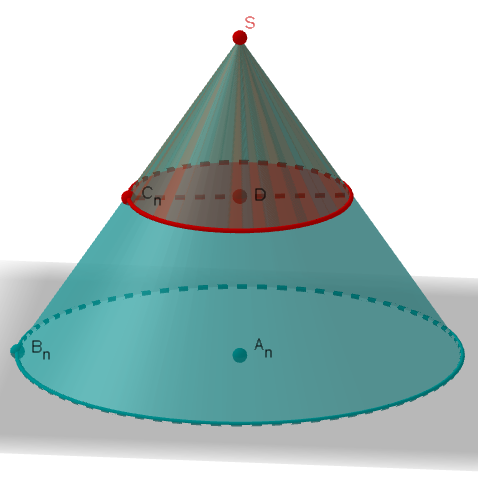
Bestätigen Sie rechnerisch, dass für das Volumen der entstehenden Rotationskörper in Abhängigkeit von gilt:
.
(2 Punkte)
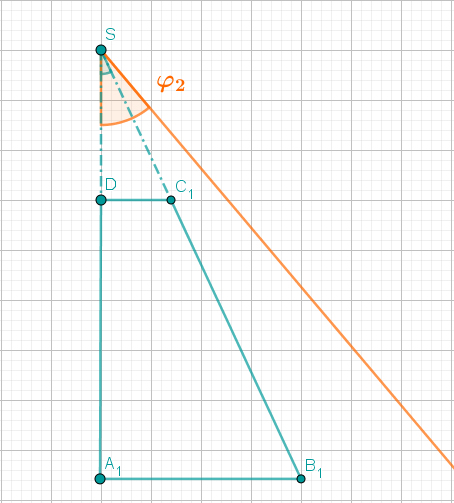
- 2
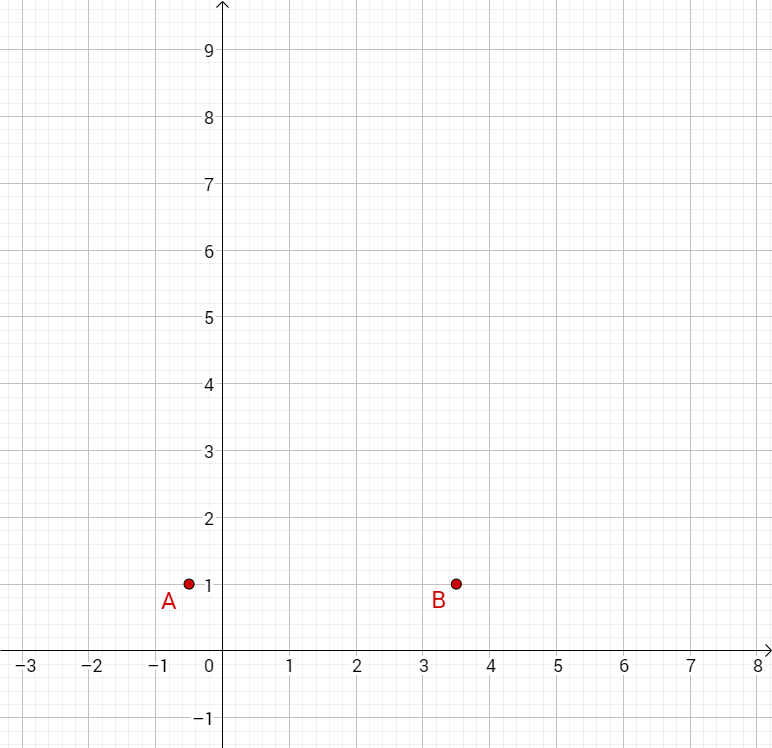
Die Punkte und legen zusammen mit Pfeilen
für Dreiecke fest.
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
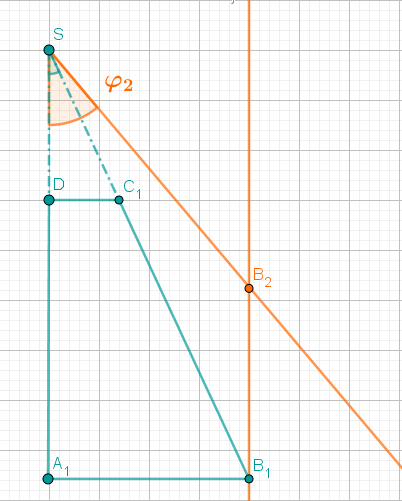
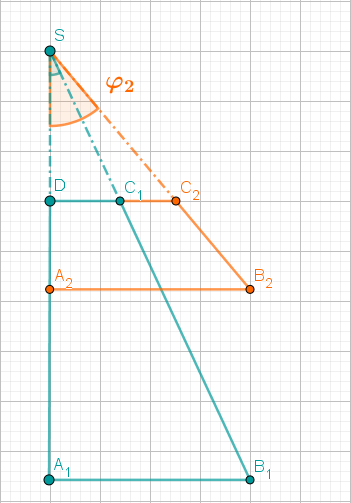
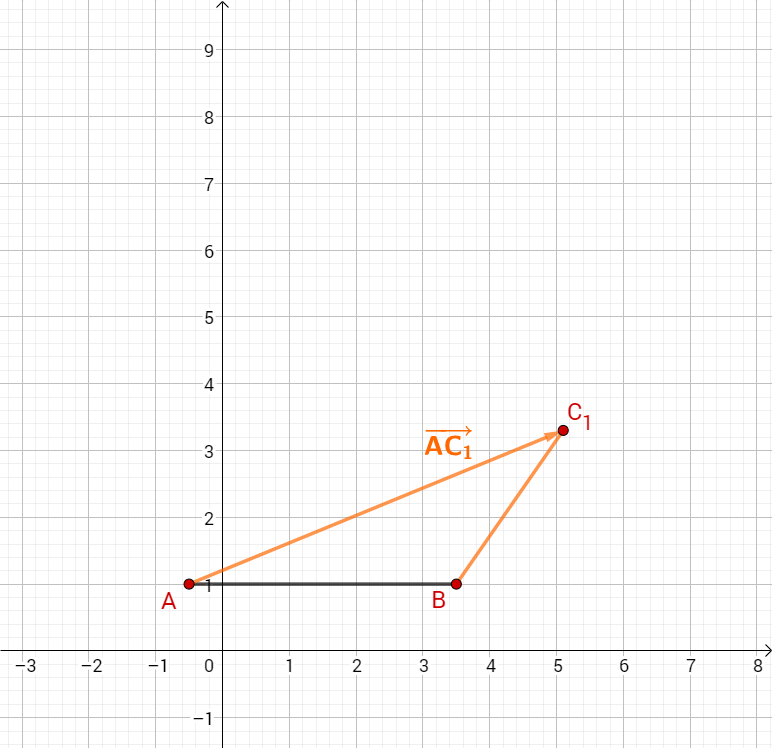
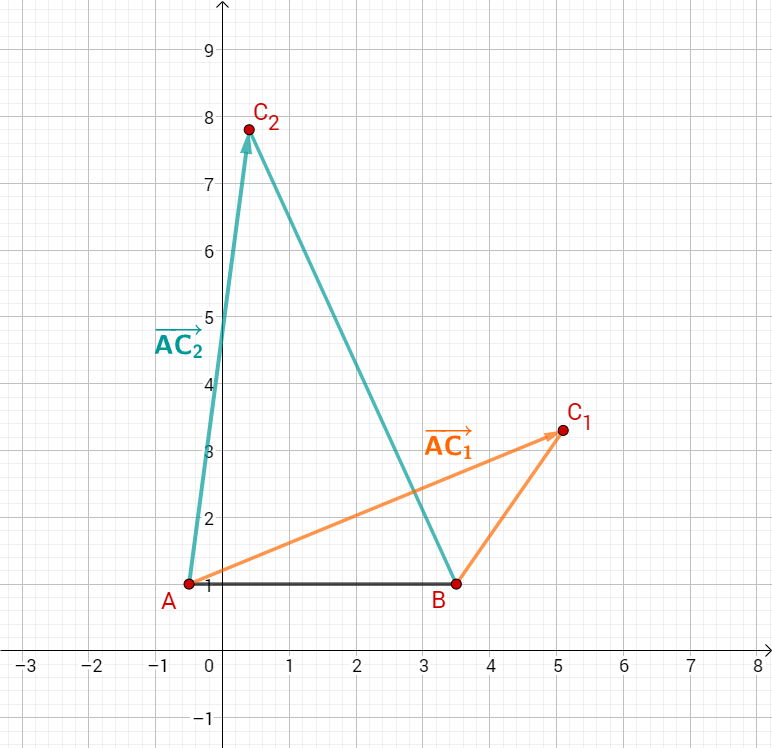
Berechnen Sie die Koordinaten der Pfeile für und für .
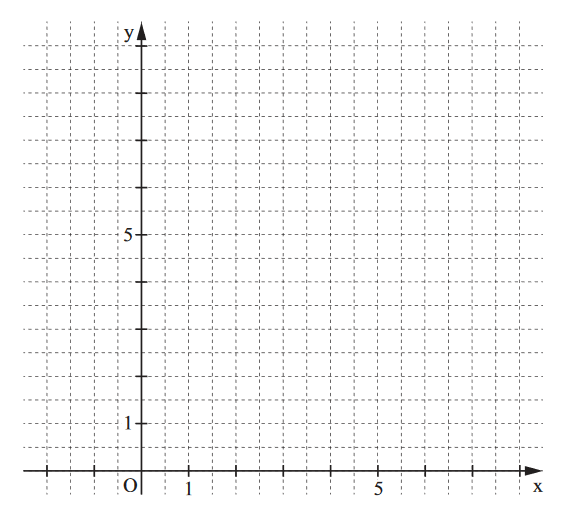
Zeichnen Sie anschließend die Dreiecke und in das Koordinatensystem ein.
3 Punkte
Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte in Abhängigkeit von gilt: .
(1 Punkt)
Bestimmen Sie rechnerisch die Gleichung des Trägergraphen der Punkte .
(2 Punkte)
Unter den Dreiecken gibt es das gleichschenklige Dreieck mit der Basis .
Ermitteln Sie das zugehörige Winkelmaß und begründen Sie durch Rechnung, dass das Dreieck nicht gleichseitig ist.
(3 Punkte)
- 3
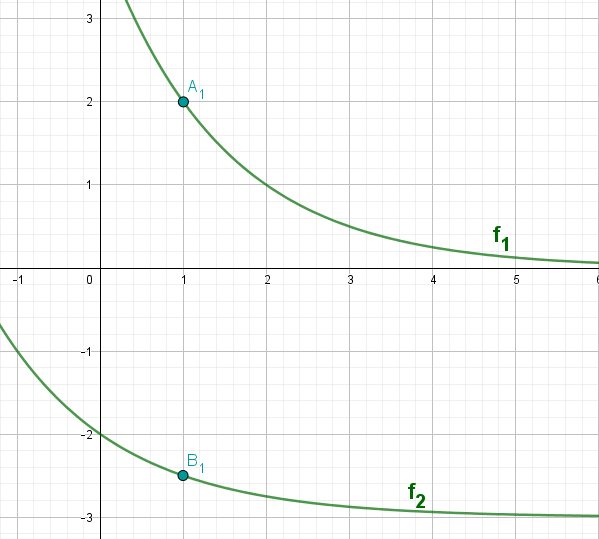
Gegeben sind die Funktionen mit der Gleichung und mit der Gleichung . Punkte auf dem Graphen zu und Punkte auf dem Graphen zu haben dieselbe Abszisse . Die Strecken sind für die Basen von gleichschenkligen Dreiecken .
Für die Höhen der Dreiecke gilt:
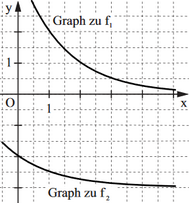
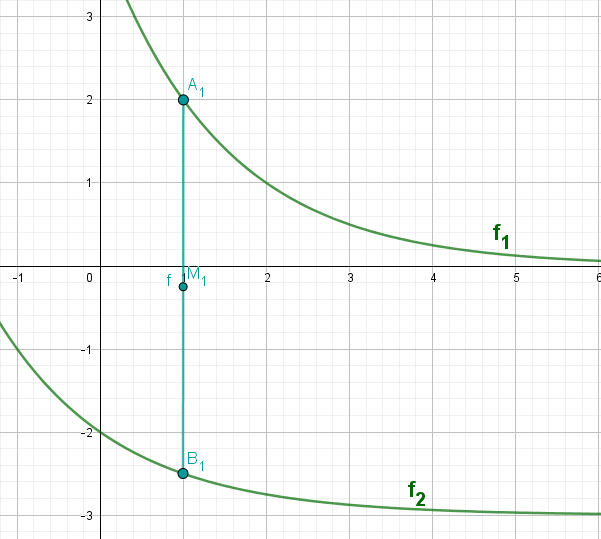
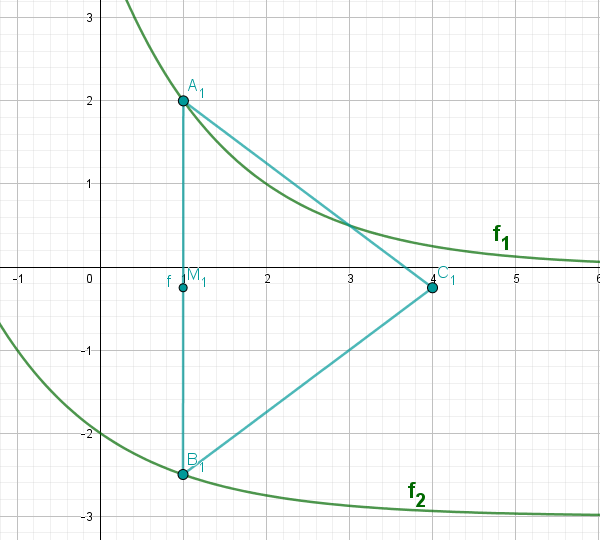
Zeichnen Sie das Dreieck für in das Koordinatensystem ein.
Zeigen Sie durch Rechnung, dass für die Länge der Strecken in Abhängigkeit von der Abszisse der Punkte gilt:
Das Dreieck hat einen Flächeninhalt von .
Berechnen Sie den zugehörigen Wert für .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?