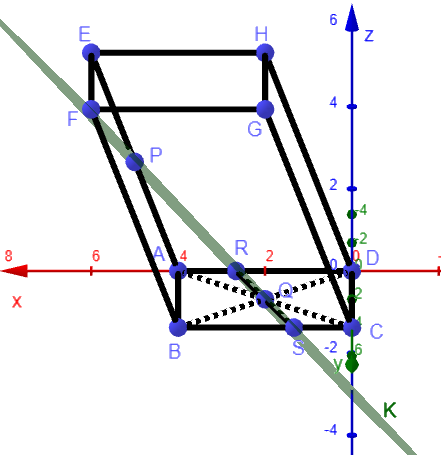
Ein Holzklotz in Form eines Spats mit quadratischer Grundfläche soll bearbeitet werden. Er ist in einem kartesischen Koordinatensystem des modellhaft so dargestellt, dass die Seiten sowie auf der - bzw. -Achse liegen und im Koordinatenursprung liegt. Die Seite wird halbiert vom Punkt . Der Diagonalenschnittpunkt der Grundfläche ist . Die Koordinaten der Punkte sind Längenangaben in der Einheit Dezimeter. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden.
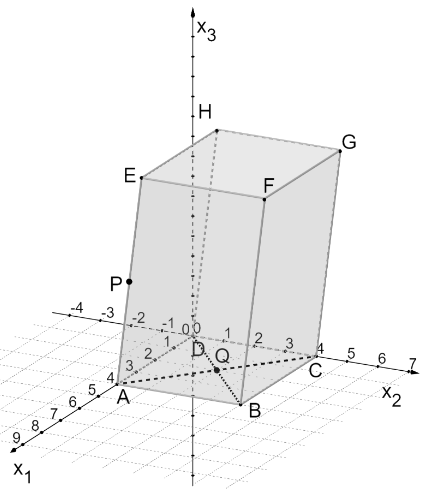
Lesen Sie die Koordinaten der Punkte und aus der Zeichnung ab. Ermitteln Sie rechnerisch die Koordinaten des Punktes [4 BE]
Die Punkte und legen die Ebene fest. Ermitteln Sie jeweils eine Gleichung von in Parameter- und Koordinatenform.
[ Mögliches Ergebnis: ] [6 BE]
Berechnen Sie den Winkel, unter dem die Gerade auf die Ebene trifft. [4 BE]
Der Holzklotz wird entlang der Ebene durchtrennt und der vordere Teil weggenommen. Dadurch ergibt sich in der Grundfläche eine Schnittkante, die die Kante im Punkt sowie die Kante im Punkt schneidet. Die Schnittfläche wird durch die Punkte und begrenzt (siehe Skizze).
Berechnen Sie die Koordinaten der Punkte und . [5 BE]
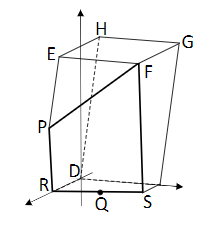
Erläutern Sie, wie Sie den Inhalt der Fläche berechnen können, ohne diese Rechnung konkret durchzuführen. [4 BE]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?