Mittelwertberechnung mithilfe eines Integrals

Geometrische Herleitung der Mittelwertberechnung mithilfe eines Integrals

Der Zusammenhang zwischen Integral und Mittelwert einer Funktion $f$ kann geometrisch hergeleitet werden.

Betrachtet wird eine Funktion $f$.

Das Integral ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$ entspricht dem orientiertem Flächeninhalt zwischen dem Graphen von $f$ und der x-Achse:

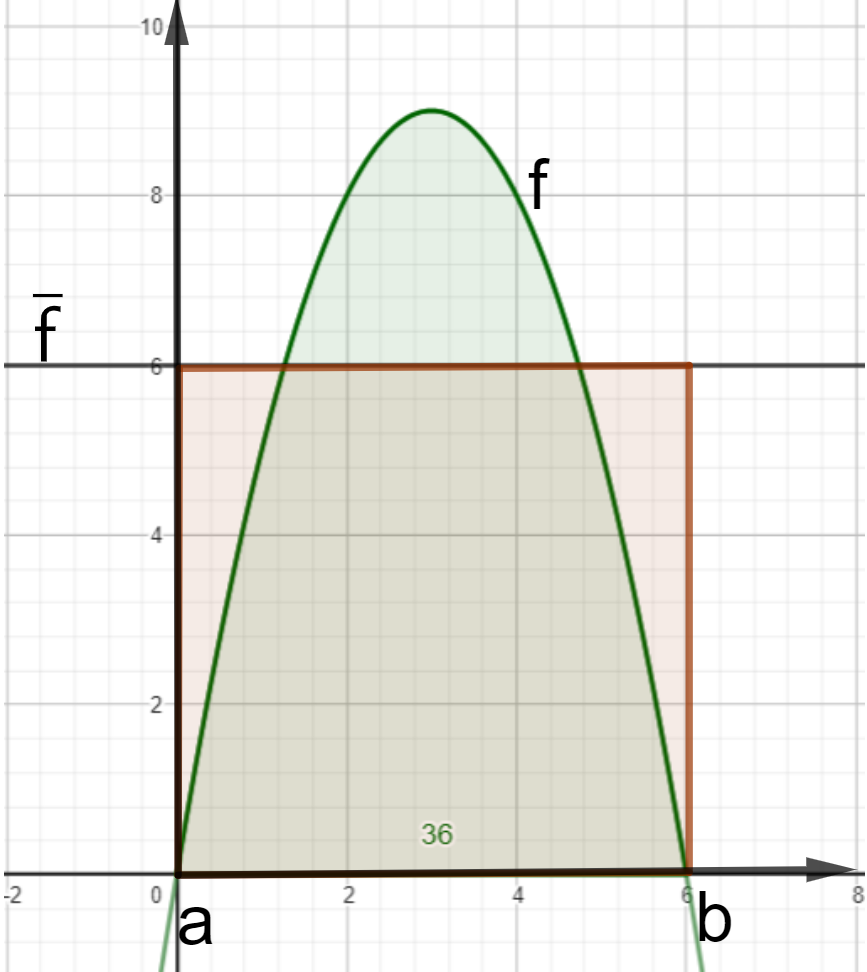
Wird die Funktion so verändert, dass sie nur den durchschnittlichen Funktionswert annimmt, dann sollte sich ihr Flächeninhalt unter dem Graphen nicht ändern.

Man kann den Durchschnittswert ${\displaystyle {\overline {f}}}$ der Funktion $f$ also darüber definieren, dass der Flächeninhalt des Rechtecks mit der Grundseite ${\displaystyle [a,b]}$ auf der x-Achse und der Höhe ${\displaystyle {\overline {f}}}$ gleich dem orientierten Flächeninhalt unter dem Graphen von $f$ ist.

Es ist also $A_{\text{Rechteck}}=(b-a)\cdot \overline {f}$ und $A_{\text{Integral}}=\displaystyle\int _{a}^{b}f(x)\,\mathrm {d} x$

Damit erhält man die Gleichung:

$A_{\text{Rechteck}}=A_{\text{Integral}}\;\Rightarrow\;(b-a)\cdot{\textstyle {\overline {f}} =\displaystyle\int _{a}^{b}f(x)\,\mathrm {d} x}$.

Die Gleichung kann umgeformt werden zu:

Anwendungsbeispiele für die Berechnung des Mittelwertes mithilfe eines Integrals

1. Durchschnittliche Geschwindigkeit

Die Funktion $v(t)$ gibt zu jedem Zeitpunkt die momentane Geschwindigkeit eines Autos in $\dfrac{\text{km}}{\text{h}}$ während einer dreistündigen Autofahrt an.

Welche durchschnittliche Geschwindigkeit hatte das Auto bei seiner Fahrt?

Es ist ${\displaystyle {\overline {v}}={\frac {1}{3-0}}\displaystyle\int _{0}^{3}v(t)\,\mathrm {d} t}$.

2. Durchschnittliche Höhe

Nachdem ein Heißluftballon zur Zeit $t=0$ seine Reisehöhe erreicht hat, wird seine Flughöhe durch die Funktion $h(t)$ beschrieben ($h$ in Metern und $t$ in Stunden).

Welche durchschnittliche Reisehöhe hatte der Ballon zwischen der $2.$ und $6.$ Stunde?

Es ist ${\displaystyle {\overline {h}}={\frac {1}{6-2}}\displaystyle\int _{2}^{6}h(t)\,\mathrm {d} t}$.

3. Durchschnittliche Temperatur

Der Temperaturverlauf der Außentemperatur wird zwischen $0$ Uhr und $24$ Uhr durch die Funktion $t(x)$ dargestellt. Wie groß ist die Durchschnittstemperatur zwischen $7.30$ Uhr und $15$ Uhr?

Es ist ${\displaystyle {\overline {t}}={\frac {1}{15-7{,}5}}\displaystyle\int _{7{,}5}^{15}f(x)\,\mathrm {d} x}$.

4. Mittlere Steigung

Gegeben ist eine Funktion $f(x)$.

Wie groß ist die mittlere Steigung des Schaubildes von $f$ im Intervall $[2;8]$?

Es ist ${\displaystyle {\overline {f'}}={\frac {1}{8-2}}\displaystyle\int _{2}^{8}f'(x)\,\mathrm {d} x}$.