Wahlteil - GTR - lernen mit Serlo!

Aufgabe 2B

Bei einer statistischen Erhebung werden in einer deutschen Großstadt die privaten

Haushalte mit mindestens einem Kind im Vorschulalter betrachtet. Diese werden im

Folgenden als „junge Haushalte“ bezeichnet. Es wird festgestellt, dass $60 %$ der jungen

Haushalte mit mindestens einem Pkw ausgestattet sind und $8 %$ der jungen Haushalte mit mindestens einem Lastenrad. In $14 %$ der jungen Haushalte ohne Pkw ist mindestens ein Lastenrad vorhanden.

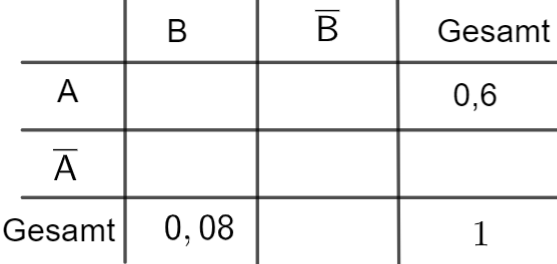
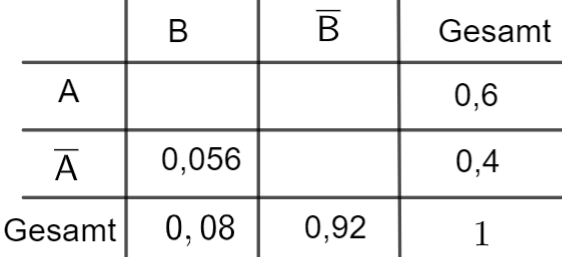
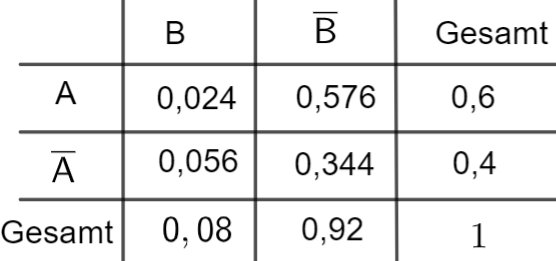
Stellen Sie den beschriebenen Sachverhalt in einer vollständig ausgefüllten
Vierfeldertafel dar. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Festlegung:
$A$ : „Ein junger Haushalt ist mit mindestens einem Pkw ausgestattet.“
$B$ : „Ein junger Haushalt ist mit mindestens einem Lastenrad ausgestattet.“
Gegeben sind $P (A) = 0,6$ und $P (B) = 0,08$ . Trage diese Werte in die Vierfeldertafel ein.
Durch Differenzbildung findest Du zwei weitere Werte.
$P(\overline{A})=1-06=0{,}4$
$P(\overline{B})=1-0{,}08=0{,}92$
Weiterhin ist bekannt, dass in $14 %$ der jungen Haushalte ohne Pkw $\left(P(\overline{A})\right)$ mindestens ein Lastenrad vorhanden ist.
$P(B\cap \overline{A})=0{,}14\cdot 0{,}4=0{,}56$
Ergänze die Vierfeldertafel mit diesen Werten.
Die restlichen Felder erhältst Du durch Differenzbildung:
$P(B\cap A)=0{,}08-0{,}056=0{,}24$
$P(\overline{B}\cap \overline{A})=0{,}4-0{,}056=0{,}344$
$P(\overline{B}\cap A)=0{,}92-0{,}344=0{,}576$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$A$ : „Ein junger Haushalt ist mit mindestens einem Pkw ausgestattet.“ $B$ : „Ein junger Haushalt ist mit mindestens einem Lastenrad ausgestattet.“
Gegeben sind $P (A) = 0,6$ und $P (B) = 0,08$ . Trage diese Werte in die Vierfeldertafel ein.
Durch Differenzbildung findest Du zwei weitere Werte.
Weiterhin ist bekannt, dass in $14 %$ der jungen Haushalte ohne Pkw $\left(P(\overline{A})\right)$ mindestens ein Lastenrad vorhanden ist. Ergänze die Vierfeldertafel mit diesen Werten. Die restlichen Felder erhältst Du durch Differenzbildung.
Beurteilen Sie für diese Großstadt die folgende Aussage: [4 BE]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter junger Haushalt mit mindestens einem Lastenrad ausgestattet ist, ist bei einem jungen Haushalt ohne Pkw mehr als dreimal so groß wie bei einem jungen Haushalt mit mindestens einem Pkw.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Beurteile für diese Großstadt die Aussage
Ein junger Haushalt ist mit mindestens einem Lastenrad ausgestattet, ist bei einem jungen Haushalt ohne Pkw... $\;\Rightarrow\;P_{\overline{A}}(B)$
Ein junger Haushalt ist mit mindestens einem Lastenrad ausgestattet, ist bei einem jungen Haushalt mit mindestens einem Pkw... $\;\Rightarrow\;P_A( B)$
Die Aussage lautet nun: $P_{\overline{A}}(B)>3\cdot P_A(B)$
$\Rightarrow\;P_{\overline{A}}(B)=\dfrac{P(B\cap \overline{A})}{P(\overline{A})}=\dfrac{0{,}056}{0{,}4}=0{,}14$
und $P_A(B)=\dfrac{P(B\cap A)}{P(A)}=\dfrac{0{,}024}{0{,}6}=0{,}04$
Damit folgt dann: $0{,}14>3\cdot 0{,}04=0{,}12$
Die Aussage ist wahr.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeige, dass gilt $P_{\overline{A}}(B)>3\cdot P_A(B)$ .
$300$ junge Haushalte dieser Großstadt werden zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als $20$ und höchstens $30$ dieser
Haushalte mit mindestens einem Lastenrad ausgestattet sind. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Bestimme die Wahrscheinlichkeit dafür, dass mehr als $20$ und höchstens $30$ dieser Haushalte mit mindestens einem Lastenrad ausgestattet sind
$X$ : Anzahl der Haushalte mit mindestens einem Lastenrad
$X$ ist binomialverteilt mit $n = 300$ und $p = 0,08$
Berechne $P(21\leq X\leq 30)$ :
$\text{binomCdf}(300{,}0.08{,}21{,}30)\approx0{,}680955$
Die Wahrscheinlichkeit, dass mehr als $20$ und höchstens $30$ dieser Haushalte mit mindestens einem Lastenrad ausgestattet sind, beträgt rund $68 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$X$ : Anzahl der Haushalte mit mindestens einem Lastenrad
$X$ ist binomialverteilt mit $n = 300$ und $p = 0,08$
Berechne $P(21\leq X\leq 30)$ .
Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem
Term
$1 − \displaystyle\sum ^{300}_{𝑘=201} \binom{300}{𝑘} \cdot 0{,}6^𝑘\cdot 0{,}4^{{300−𝑘}}$
berechnet werden kann. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $1 − \displaystyle\sum^{300}_{𝑘=201} \binom{300}{𝑘}\cdot 0{,}6^𝑘 \cdot 0{,}4^{300−𝑘}$ berechnet werden kann
Im Term tritt die Wahrscheinlichkeit $0,6$ auf. Das ist die Wahrscheinlichkeit dafür, dass ein junger Haushalt mit mindestens einem Pkw ausgestattet ist.
Weiterhin entnimmt man dem Term $n = 300$ und $k = 201$ .
Der Summenterm berechnet somit die Wahrscheinlichkeit $P(X\geq 201)$ .
Dann ist die Gegenwahrscheinlichkeit $1-P(X\geq 201)=P(X\leq 200)$
$P(X\leq 200)$ besagt, dass höchstens 200 dieser Haushalte mit mindestens einem Pkw ausgestattet sind.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Im Term tritt die Wahrscheinlichkeit $0,6$ auf. Das ist die Wahrscheinlichkeit dafür, dass ein junger Haushalt mit mindestens einem Pkw ausgestattet ist.
Weiterhin entnimmt man dem Term $n = 300$ und $k = 201$ . Der Summenterm berechnet somit die Wahrscheinlichkeit $P(X\geq 201)$ .
Was ist dann die Gegenwahrscheinlichkeit?
Betrachtet werden Vorderrad- und Hinterradreifen für Lastenräder. Die Laufleistung gibt die Gesamtstrecke an, bis ein Reifen unbrauchbar wird. Die Zufallsgröße $V$ beschreibt die Laufleistung in Kilometern ( $\text{km}$ ) der Vorderradreifen eines Herstellers, die Zufallsgröße $H$ die Laufleistung der Hinterradreifen desselben Herstellers. Beide Zufallsgrößen sind normalverteilt. Es gilt:
$\mu_V = 6800\;\text{km}$ und $\sigma_V = 530\;\text{km}$
$\mu_H = 4600\;\text{km}$ und $\sigma_H= 480\;\text{km}$
Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter
Vorderradreifen eine Laufleistung hat, die um höchstens $600\;\text{km}$ vom Erwartungswert
für diese Laufleistung abweicht. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Vorderradreifen eine Laufleistung hat, die um höchstens $600\;\text{km}$ vom Erwartungswert für diese Laufleistung abweicht
Gesucht ist $P(|V-\mu_V|\leq 600)$ :
Gegeben sind $\mu_V = 6800\;\text{km}$ und $\sigma_V = 530\;\text{km}$ .
Dann ist folgende Wahrscheinlichkeit gesucht:
$P(6800-600\leq X\leq6800+600)=P(6200\leq X\leq7400)$
$P(6200\leq X\leq7400)=\Phi\left(\dfrac{7400-6800}{530}\right)-\Phi\left(\dfrac{6200-6800}{530}\right)$
$\Rightarrow\;\Phi\left(\dfrac{600}{530}\right)-\Phi\left(-\dfrac{600}{530}\right)=2\cdot \Phi\left(\dfrac{600}{530}\right)-1\approx2\cdot0{,}8712-1=0{,}7424$
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Vorderradreifen eine Laufleistung hat, die um höchstens $600\;\text{km}$ vom Erwartungswert für diese Laufleistung abweicht, beträgt rund $74 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gegeben sind $\mu_V = 6800\;\text{km}$ und $\sigma_V = 530\;\text{km}$ .
Gesucht ist $P(|V-\mu_V|\leq 600)$ $\;\Rightarrow\;P(6200\leq X\leq7400)$ .
Beachte $\Phi(z)- \Phi(-z)=2\cdot \Phi(z)-1$ .
Begründen Sie, dass die folgende Aussage für die Vorderrad- und Hinterradreifen wahr ist: [4 BE]
Die Laufleistung, die ein zufällig ausgewählter Vorderradreifen gemäß dem Modell mit der Wahrscheinlichkeit von $90 %$ übertreffen wird, wird ein zufällig ausgewählter Hinterradreifen nahezu mit Sicherheit unterschreiten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Begründe, dass die Aussage für die Vorderrad- und Hinterradreifen wahr ist
Für den Vorderradreifen wird behauptet:
$P (V > c) = 0,9$
Es gilt: $P(X\geq a)=1-\Phi\left(\dfrac{a-\mu}{\sigma}\right)$
Dann folgt:
$P(V > c) = 1-\Phi\left(\dfrac{c-\mu_V}{\sigma_V}\right)=0{,}9$
$0{,}1=\Phi\left(\dfrac{c-6800}{530}\right)$
$\Phi(z)=0{,}1$ liefert $z\approx -1{,}282$ und damit folgt die Gleichung:
$-1{,}282=\dfrac{c-6800}{530}$
Dann ist $c=-1{,}282\cdot 530+6800\approx 6120$ .
Betrachtet man nun einen Hinterradradreifen, dann kann $P (H < 6120)$ berechnet werden:
Es gilt $\mu_H = 4600\;\text{km}$ und $\sigma_H = 480\;\text{km}$ .
$P(H < 6120)= \Phi\left(\dfrac{6120-4600}{480}\right)\approx\Phi(3{,}167)\approx0{,}9992$
Ein zufällig ausgewählter Hinterradradreifen hat wegen $P(H < 6120) \approx0{,}9992$ mit einer sehr großen Wahrscheinlichkeit eine Laufleistung von weniger als $6120⁡\;\text{km}$ .
Die Aussage ist wahr.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für den Vorderradreifen wird behauptet: $P (V > c) = 0,9$
Es gilt: $P(X\geq a)=1-\Phi\left(\dfrac{a-\mu}{\sigma}\right)$
Berechne mit den gegebenen Werten $c$ .
Für einen Hinterradradreifen kann dann $P (H < c)$ berechnet werden.
Die Zufallsgröße $Z$ beschreibt die
Laufleistung in km der Hinterradreifen
eines anderen Herstellers.
$Z$ wird als normalverteilt mit dem Erwartungswert $\mu_Z$ und der Standardabweichung $\sigma_Z$ angenommen.
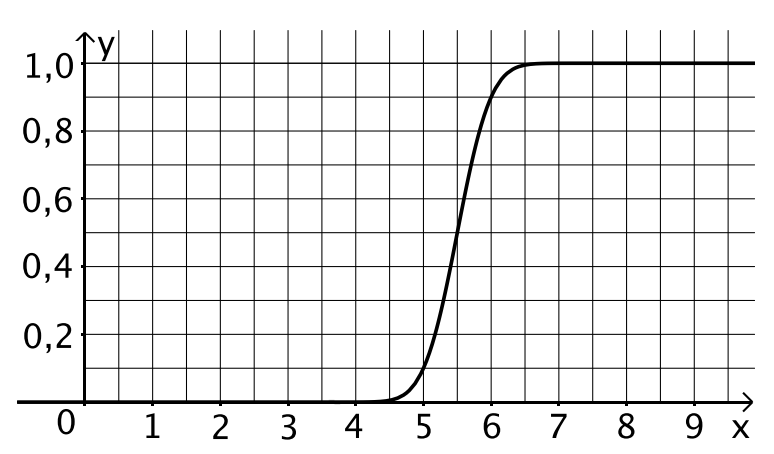
Die Abbildung stellt den Graphen der
Funktion $𝑓$ mit $f(x) = P(Z≤ 1000 \cdot x)$ dar. Ermitteln Sie die Werte von $\mu_Z$ und $\sigma_Z$ jeweils in km. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Ermittle die Werte von $\mu_Z$ und $\sigma_Z$ jeweils in km
Aus dem Graphen entnimmt man $f (5,5) = 0,5$ .
Mit $f(x)=P(Z \leq 1000 \cdot x)$ folgt dann:
$0{,}5 =P(Z \leq 1000 \cdot 5{,}5)=P(Z \leq 5500)=\Phi\left(\dfrac{5500-\mu_z}{\sigma_z}\right)$
Andererseits ist $\Phi(0)=0{,}5\;\Rightarrow\;\dfrac{5500-\mu_z}{\sigma_z}=0$ .
$\dfrac{5500-\mu_z}{\sigma_z}=0\;\Rightarrow\;\mu_z=5500$
Zur Bestimmung von $\sigma_z$ wird ein zweiter Punkt des Graphens benötigt.
Es ist $f (6) = 0,9$ .
$f(6)=0{,}9\;\Rightarrow\;P(Z \leq 1000 \cdot 6)=P(Z \leq 6000)=\Phi\left(\dfrac{6000-5500}{\sigma_z}\right)=0{,}9$
Mit $\Phi\left(\dfrac{6000-5500}{\sigma_z}\right)=0{,}9$ folgt $\Phi(z)=0{,}9$ und $z\approx 1{,}283$ .
Dann erhält man:
$\dfrac{6000-5500}{\sigma_z}\approx1{,}283\;\Rightarrow\;\sigma_z=\dfrac{500}{1{,}283}\approx389{,}7$
Damit sind $\mu_z=5500\;\text{km}$ und $\sigma_z=390\;\text{km}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Aus dem Graphen entnimmt man $f (5,5) = 0,5$ . Berechne damit $\mu_z$ .
Entnimm dem Graphen einen weiteren Punkt und berechne $\sigma_z$ .

Aufgabe 2B

Hast du eine Frage oder Feedback?

Beurteile für diese Großstadt die Aussage

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit dafür, dass mehr als 202020 und höchstens 303030 dieser Haushalte mit mindestens einem Lastenrad ausgestattet sind

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Vorderradreifen eine Laufleistung hat, die um höchstens 600 km600\;\text{km}600km vom Erwartungswert für diese Laufleistung abweicht

Hast du eine Frage oder Feedback?

Begründe, dass die Aussage für die Vorderrad- und Hinterradreifen wahr ist

Hast du eine Frage oder Feedback?

Ermittle die Werte von μZ\mu_ZμZ​ und σZ\sigma_ZσZ​ jeweils in km

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit dafür, dass mehr als $20$ und höchstens $30$ dieser Haushalte mit mindestens einem Lastenrad ausgestattet sind

Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Vorderradreifen eine Laufleistung hat, die um höchstens $600\;\text{km}$ vom Erwartungswert für diese Laufleistung abweicht

Ermittle die Werte von $\mu_Z$ und $\sigma_Z$ jeweils in km