Wahlteil - CAS - lernen mit Serlo!

Aufgabe 3B

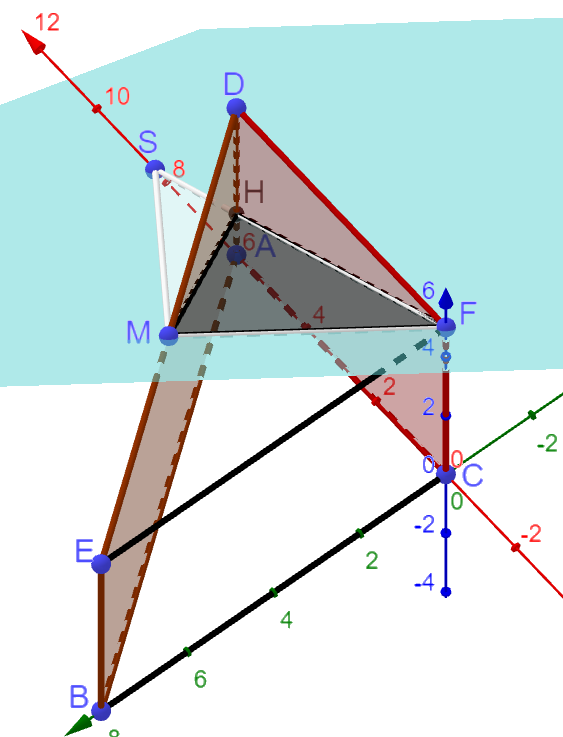
Gegeben sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 ∣ 0 ∣ 0), D (6 ∣ 0 ∣ 5)$ , $E (0 ∣ 8 ∣ 5)$ und $F (0 ∣ 0 ∣ 5)$ sowie der Punkt $M (3 ∣ 4 ∣ 5)$ (vgl. Abbildung 1).

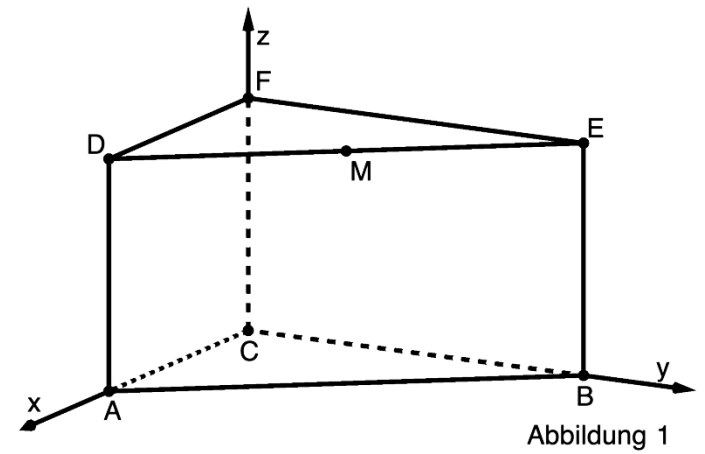
Berechnen Sie den Inhalt der Oberfläche des Prismas. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
Berechne den Inhalt der Oberfläche des Prismas
Für die Oberflächenberechnung werden verschiedene Vektoren und ihre Beträge benötigt.
$\overrightarrow{DE}=\overrightarrow{OE}-\overrightarrow{OD}=\begin{pmatrix}0\\8\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-6\\8\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DE}\Big\vert=\sqrt{(-6)^2+8^2+0}=\sqrt{100}=10$
$\overrightarrow{DF}=\overrightarrow{OF}-\overrightarrow{OD}=\begin{pmatrix}0\\0\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-6\\0\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DF}\Big\vert=6$
$\overrightarrow{FE}=\overrightarrow{OE}-\overrightarrow{OF}=\begin{pmatrix}0\\8\\5\end{pmatrix}-\begin{pmatrix}0\\0\\5\end{pmatrix}=\begin{pmatrix}0\\8\\0\end{pmatrix}\\\Big\vert\overrightarrow{FE}\Big\vert=8$
Die Höhe des Prismas ist $h = 5$ .
Dann folgt für den Oberflächeninhalt des Prismas:
$O_\text{Prisma}=\Big\vert\overrightarrow{DF}\Big\vert\cdot h+\Big\vert\overrightarrow{EF}\Big\vert\cdot h+\Big\vert\overrightarrow{DE}\Big\vert\cdot h+2\cdot \dfrac{1}{2}\cdot \Big\vert\overrightarrow{DF}\Big\vert\cdot \Big\vert\overrightarrow{EF}\Big\vert$
$O_\text{Prisma}=(6+8+10)\cdot 5+2\cdot \dfrac{1}{2}\cdot 6\cdot 8=168$
Der Inhalt der Oberfläche des Prismas beträgt $168\; \text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Vektoren $\overrightarrow{DE}$ , $\overrightarrow{DF}$ und $\overrightarrow{FE}$ und ihre Beträge.
Die Höhe des Prismas ist die z-Koordinate eines in der Deckfläche liegenden Punktes.
Begründen Sie, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$
liegen. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einführung zum Kreis
Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen
Berechne die Vektoren $\overrightarrow{DM}, \overrightarrow{FM}$ und $\overrightarrow{EM}$ , sowie ihre Beträge.
$\overrightarrow{DM}=\overrightarrow{OM}-\overrightarrow{OD}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-3\\4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DM}\Big\vert=\sqrt{(-3)^2+4^2+0}=\sqrt{25}=5$
$\overrightarrow{FM}=\overrightarrow{OM}-\overrightarrow{OF}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}0\\0\\5\end{pmatrix}=\begin{pmatrix}3\\4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{FM}\Big\vert=\sqrt{3^2+4^2+0}=\sqrt{25}=5$
$\overrightarrow{EM}=\overrightarrow{OM}-\overrightarrow{OE}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}0\\8\\5\end{pmatrix}=\begin{pmatrix}3\\-4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{EM}\Big\vert=\sqrt{3^2+(-4)^2+0}=\sqrt{25}=5$
Es gilt: $\Big\vert\overrightarrow{DM}\Big\vert= \Big\vert\overrightarrow{FM}\Big\vert= \Big\vert\overrightarrow{EM}\Big\vert=5$
Alle Punkte liegen zusammen mit $M$ in einer Ebene und haben den gleichen Abstand $5$ vom Punkt $M$ und liegen deshalb auf einem Kreis um $M$ mit dem Radius $5$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Vektoren $\overrightarrow{DM}, \overrightarrow{FM}$ und $\overrightarrow{EM}$ , sowie ihre Beträge.
Berechnen Sie den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
Berechne den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt
Berechne den Vektor $\overrightarrow{MA}$ :
$\overrightarrow{MA}=\overrightarrow{OA}-\overrightarrow{OM}=\begin{pmatrix}6\\0\\0\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}3\\-4\\-5\end{pmatrix}$
Der Vektor $\vec n=\begin{pmatrix}1\\0\\0\end{pmatrix}$ .
Für den Winkel zwischen den beiden Vektoren gilt:
$\cos\alpha=\dfrac{|\vec{n}\circ\overrightarrow{MA}|}{|\vec{n}|\cdot|\overrightarrow{MA}|}=\dfrac{\left|\begin{pmatrix}1\\0\\0\end{pmatrix}\circ\begin{pmatrix}3\\-4\\-5\end{pmatrix}\right|}{1\cdot \sqrt{3^2+(-4)^2+(-5)^2}}=\dfrac{3}{\sqrt{50}}$
$\alpha=\cos^{-1}\left(\dfrac{3}{\sqrt{50}}\right)\approx 64{,}9^\circ$
Der Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt, beträgt rund $65^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Vektor $\overrightarrow{MA}$ .
Die x-Achse wird durch den Vektor $\begin{pmatrix}1\\0\\0\end{pmatrix}$ dargestellt.
Für den Winkel zwischen zwei Vektoren gilt: $\cos\alpha=\dfrac{|\vec{a}\circ\vec{b}|}{|\vec{a}|\cdot|\vec{b}|}$
Durch
$\def\arraystretch{1.25} \vec x= \left(\begin{array}{} 0\\0 \\5 \end{array}\right) + \lambda \left(\begin{array}{}3 \\4 \\0 \end{array}\right) + \mu \left(\begin{array}{} 7{,}5\\ 0\\-5 \end{array}\right)$
mit $\lambda, \mu \in\mathbb{R}$ ist die Ebene $H$ gegeben.
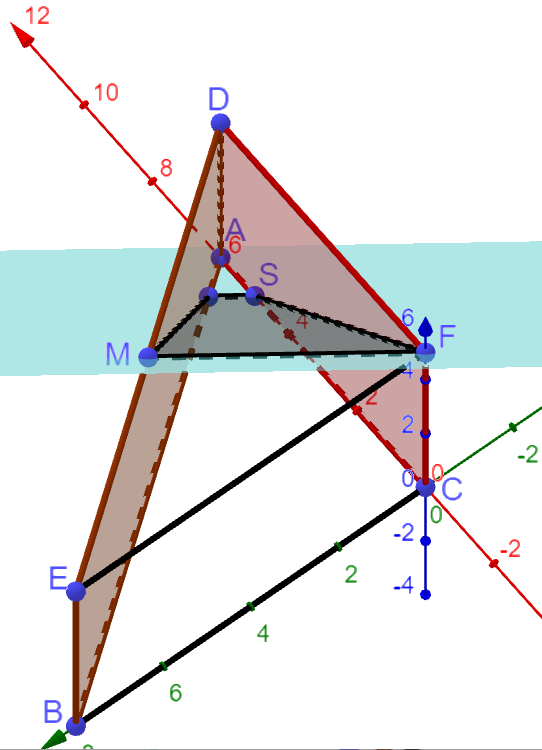
Die Punkte $M, F$ und $S (7,5 ∣ 0 ∣ 0)$ liegen in der Ebene $H$ (vgl. Abbildung 2).
Im Folgenden sind zwei Schritte zum Lösen einer Aufgabe angegeben, die im Zusammenhang mit den betrachteten geometrischen Objekten steht:
$\def\arraystretch{1.25} \left(\begin{array}{} 6\\0 \\1\end{array}\right) = \left(\begin{array}{} 0\\0 \\5 \end{array}\right) + \lambda \left(\begin{array}{} 3\\4 \\0 \end{array}\right) + \mu \left(\begin{array}{} 7{,}5\\0 \\-5 \end{array}\right)$
$\def\arraystretch{1.25} \left(\begin{array}{} 6\\0 \\1 \end{array}\right) = \left(\begin{array}{} 6\\0 \\0 \end{array}\right) + r\left(\begin{array}{} 0\\0 \\5 \end{array}\right)$ mit $r \in\mathbb{R}$
Geben Sie eine passende Aufgabenstellung an. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung von Punkten, Geraden und Ebenen
Gib eine passende Aufgabenstellung an
In Gleichung $\mathrm{(I)}$ wird eine Punktprobe durchgeführt. Es wird geprüft, ob der Punkt $(6 ∣ 0 ∣ 1)$ in der Ebene $H$ liegt.
In Gleichung $\mathrm{(II)}$ wird ebenfalls eine Punktprobe durchgeführt. Es wird geprüft, ob der Punkt $(6 ∣ 0 ∣ 1)$ auf der Geraden durch die Punkte $A$ und $D$ liegt.
Aufgabenstellung: Untersuche, ob der Punkt $(6 ∣ 0 ∣ 1)$ sowohl in der Ebene $H$ als auch auf der Geraden durch $A$ und $D$ liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es werden zwei Punktproben für den Punkt $(6 ∣ 0 ∣ 1)$ durchgeführt.
Wo soll der Punkt liegen?
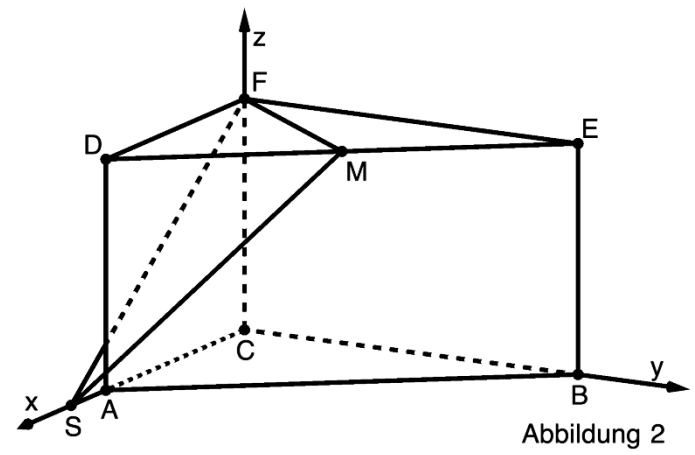
Anstelle des Punkts $S$ werden nun Punkte $S_{t} (t ∣ 0 ∣ 0)$ mit $t\geq 0$ auf der x-Achse betrachtet.
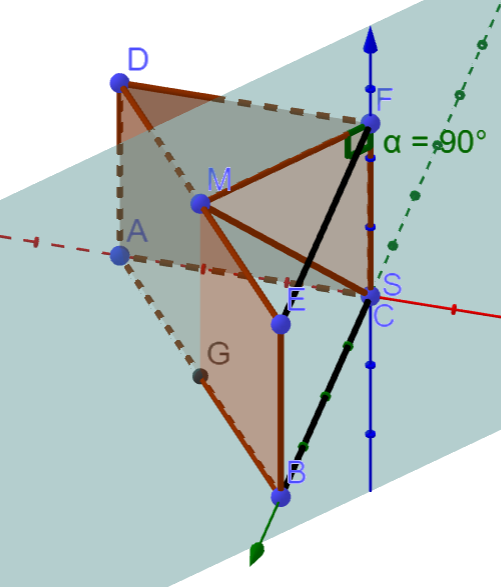
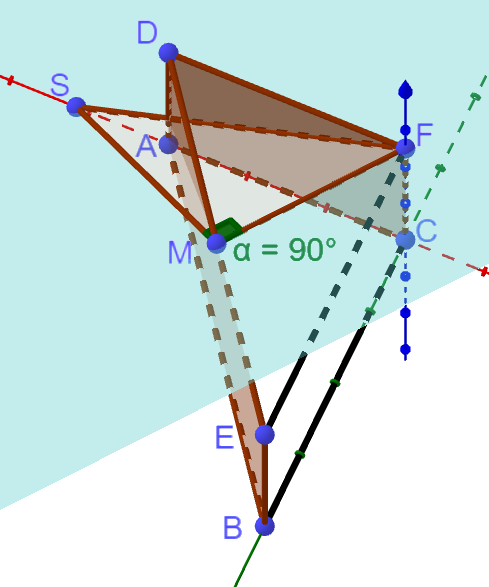
Für jeden Wert von $t$ schneidet die Ebene durch die Punkte $M, F$ und $S_{t}$ das Prisma
$A B C D E F$ in einem Vieleck.
Geben Sie die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an. [4 BE]

Gib die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an
Maßgebend für die Art des Vielecks ist die x-Koordinate von $A$ : $x = 6$
Für $t\geq 6$ besitzt das Vieleck drei Ecken.
Für $0 \leq t < 6$ besitzt das Vieleck vier Ecken.
Zur Veranschaulichung: Vieleck mit drei Ecken
Hier hat $t$ den Wert $\dfrac{25}{3}>6$ .
Das weiß umrandete Dreieck liegt in der Ebene durch die Punkte $M, F$ und $S_{t}$ .
Das schwarze Dreieck ist die Schnittfläche der Ebene mit dem Prisma.
Zur Veranschaulichung: Vieleck mit vier Ecken
Hier hat $t$ den Wert $5 < 6$ .
Das schwarze Viereck ist die Schnittfläche der Ebene mit dem Prisma.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Maßgebend für die Art des Vielecks ist die x-Koordinate von $A$ : $x = 6$
Bestimmen Sie die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Bestimme die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist
Möglichkeit 1
Für $t = 0$ liegt der Punkt $S$ auf dem Punkt $C$ . Dann befindet sich ein rechter Winkel im Punkt $F$ .
Skizze zur Veranschaulichung:
Möglichkeit 2
Berechne das Skalarprodukt der beiden Vektoren $\overrightarrow{MF}$ und $\overrightarrow{MS_t}$ . Es muss für einen rechten Winkel bei $M$ gleich null sein.
$\overrightarrow{MF}=\overrightarrow{OF}-\overrightarrow{OM}=\begin{pmatrix}0\\0\\5\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}-3\\-4\\0\end{pmatrix}$
$\overrightarrow{MS_t}=\overrightarrow{OS_t}-\overrightarrow{OM}=\begin{pmatrix}t\\0\\0\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}t-3\\-4\\-5\end{pmatrix}$
$\overrightarrow{MF}\circ \overrightarrow{MS_t}=\begin{pmatrix}-3\\-4\\0\end{pmatrix}\circ \begin{pmatrix}t-3\\-4\\-5\end{pmatrix}=-3\cdot(t-3)+(-4)\cdot(-4)=0$
$\Rightarrow\; -3t+9+16=0\;\Rightarrow\;t=\dfrac{25}{3}$
Für $t=\dfrac{25}{3}$ liegt der rechte Winkel im Punkt $M$ .
Skizze zur Veranschaulichung:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Möglichkeit 1:
Überlege Dir, wo der Punkt $S$ für $t = 0$ liegt.
Möglichkeit 2:
Berechne das Skalarprodukt der beiden Vektoren $\overrightarrow{MF}$ und $\overrightarrow{MS_t}$ .

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

Aufgabe 3B

Berechne den Inhalt der Oberfläche des Prismas

Hast du eine Frage oder Feedback?

Begründe, dass die Punkte D,ED, ED,E und FFF auf einem Kreis mit dem Mittelpunkt MMM liegen

Hast du eine Frage oder Feedback?

Berechne den Winkel, den die Strecke AM‾\overline{AM}AM mit der x-Achse einschließt

Hast du eine Frage oder Feedback?

Gib eine passende Aufgabenstellung an

Hast du eine Frage oder Feedback?

Gib die Anzahl der Ecken des Vielecks in Abhängigkeit von ttt an

Hast du eine Frage oder Feedback?

Bestimme die beiden Werte von ttt, für die das Dreieck MFStMFS_tMFSt​ rechtwinklig ist

Möglichkeit 1

Möglichkeit 2

Hast du eine Frage oder Feedback?

Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen

Berechne den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt

Gib die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an

Bestimme die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist