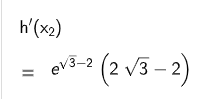Abiturprüfungen Mathe gA mit Lösungen

1

Aufgabe 1A

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit

$f(x) =\frac3{1000}\cdot x^4 −\frac8{100}\cdot x^3 +\frac6{10}\cdot x^2$ .

Abbildung 1 zeigt den Graphen von $f$ sowie den Punkt $P(0|-\frac58).$

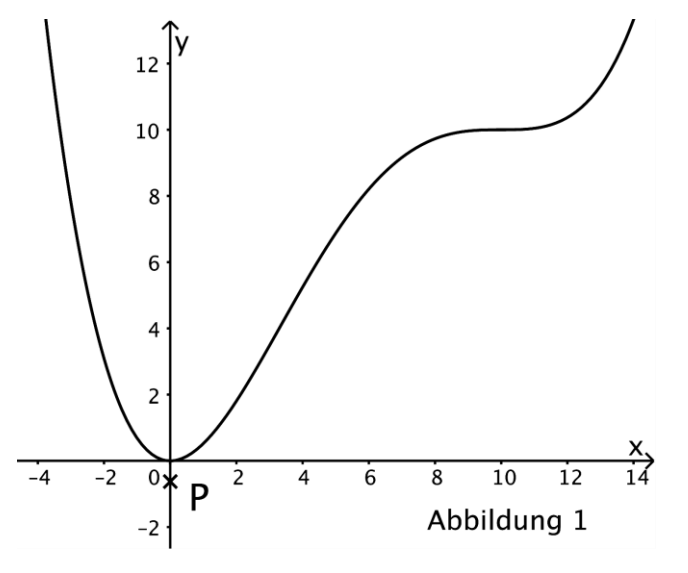
Der Graph von $f$ besitzt den Tiefpunkt $(0 ∣ 0)$ .
Zeigen Sie rechnerisch, dass der Graph von $f$ keine weiteren Extrempunkte besitzt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Zeige rechnerisch, dass der Graph von $f$ keine weiteren Extrempunkte besitzt
Löse $(f^{'} (x) = 0)$ mit den beiden Lösungen $x = 0$ oder $x = 10$
Bei $x = 0$ besitzt der Graph von $f$ den Tiefpunkt $(0 ∣ 0)$ .
$x = 10$ :
Berechne $f^{''} (10)$ und $f^{'''} (10)$ :
$f^{''} (10) = 0$ und $f'''(10)=\dfrac{6}{25}>0$
Bei $x = 10$ besitzt der Graph von $f$ einen Terrassenpunkt (Sattelpunkt) und damit keine weiteren Extrempunkte.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse $(f^{'} (x) = 0)$ $\;\Rightarrow\;x_1=0$ und $x_{2}$
Berechne $f^{''} (x_{2})$ und $f^{'''} (x_{2})$ .
Die Gerade durch die Punkte $P(0|−\frac58)$ und $Q (−\frac14|−1)$ wird mit $t$ bezeichnet.
Ermitteln Sie eine Gleichung von $t$ . Weisen Sie rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ ist. [5 BE]
[Zur Kontrolle: Gleichung von $𝑡: 𝑦 =\frac32𝑥 −\frac58$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Ermittle eine Gleichung von $t$
Aus $P$ entnimmt man den y-Achsenabschnitt $b=-\dfrac{5}{8}$ .
Setze in $y=m \cdot x+b= m \cdot x-\dfrac{5}{8}$ die Koordinaten von $Q$ ein:
$-1=m \cdot \left(-\dfrac{1}{4}\right)-\dfrac{5}{8}\;\Rightarrow\;-\dfrac{3}{8}=m \cdot \left(-\dfrac{1}{4}\right)\;\Rightarrow\;m=\dfrac{3}{2}$
Damit erhält man:
$\displaystyle t:y=\dfrac{3}{2}\cdot x-\dfrac{5}{8}$
Weise rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ ist
$t$ ist Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ , wenn:
$f (5) = t (5)$
$f^{'} (5) = m_{t}$
Berechne: $f (5) = 6,875$ und $t(5)=6{,}875 \;\Rightarrow\;f(5)=t(5)\;\checkmark$
$f'(5)=\dfrac{3}{2}$ und $m_t=\dfrac{3}{2}\;\Rightarrow\;f'(5)=m_t\;\checkmark$
Beide Bedingungen sind erfüllt:
$\Rightarrow\;t$ ist die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Aus $P$ entnimmt man den y-Achsenabschnitt $b$ .
Setze in $y=m \cdot x+b$ die Koordinaten von $Q$ ein.
Teil 2
$t$ ist Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ , wenn $f (5) = t (5)$ und $f^{'} (5) = m_{t}$
Der Graph von $f$ und die Tangente $t$ schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechnen Sie den Inhalt dieser Fläche. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne den Inhalt dieser Fläche
Für die Integrationsgrenzen berechne $f\cap t$ :
Löse $($ $f (x) = t (x)$ $)$ :
Man erhält die Lösungen $x_1=\dfrac{-5\sqrt{22}+25}{3}$ , $x_{2} = 5$ und $x_3=\dfrac{5\sqrt{22}+25}{3}$ .
Bei $x_{2} = 5$ berühren sich $f$ und $t$ (siehe Aufgabe b).
Berechne den Flächeninhalt:
$A=\displaystyle\int_{x_1}^{x_3}(t(x)-f(x))\;\mathrm{d}x=\dfrac{770}{81}\cdot \sqrt{22}\approx44{,}6$
Der gesuchte Flächeninhalt beträgt rund $44{,}6 \;\text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für die Integrationsgrenzen berechne $f (x) = t (x)$ $\;\Rightarrow\;x_1,x_2$ und $x_{3}$ .
Bei $x_{2}$ berühren sich $f$ und $t$ .
Berechne den Flächeninhalt: $A=\displaystyle\int_{x_1}^{x_3}(t(x)-f(x))\;\mathrm{d}x$
Der Graph der in $\mathbb{R}$ definierten Funktion $g$ kann aus dem Graphen von $f$ erzeugt
werden.
Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des
Graphen von $f$ erzeugt und für alle $x\in\mathbb{R}$ gilt $𝑔(𝑥) = 𝑎 \cdot 𝑓(𝑏 ⋅ 𝑥)$ mit $a,b \in\mathbb{R}^+$
Geben Sie in diesem Zusammenhang die Bedeutung von $a$ und $b$ an und
berechnen Sie die Werte von $𝑎$ und $𝑏$ . [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
Gib in diesem Zusammenhang die Bedeutung von $a$ und $b$ an
Die Funktion $f$ wird mit dem Faktor $a$ in y-Richtung gestreckt und anschließend mit dem Faktor $\dfrac{1}{b}$ in x-Richtung gestreckt.
$\underbrace{f\xrightarrow{\cdot a}a\cdot f}_\text{Streckung in y-Richt.mit Faktor a}\;\underbrace{\xrightarrow{f(b\cdot x)}a\cdot f(b\cdot x)}_{\text{Streckung in x-Richt.mit Faktor\;}\frac{1}{b}}=g(x)$
Berechne die Werte von $𝑎$ und $𝑏$
Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des
Graphen von $f$ erzeugt:
$\Rightarrow\; g(12)=a\cdot f(10)\;\Rightarrow\;12=a\cdot 10\;\Rightarrow\;a=\dfrac{6}{5}$
Weiterhin folgt: $12=\dfrac{1}{b}\cdot 10\;\Rightarrow\;b=\dfrac{5}{6}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Es handelt sich einmal um eine Streckung in y-Richtung und um eine Streckung in x-Richtung.
Teil 2
Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des Graphen von $f$ erzeugt. Stelle zwei Gleichungen zur Berechnung von $a$ und $b$ auf.
Zwei Radfahrer starten gleichzeitig nebeneinander.
Die Geschwindigkeit von Radfahrer $F$ wird in den ersten $10$ Sekunden (s) nach dem Start durch die Funktion $f$ mit $f(x) =\frac3{1000}\cdot x^4 −\frac8{100}\cdot x^3 +\frac6{10}\cdot x^2$
beschrieben.
Die Geschwindigkeit von Radfahrer $H$ wird in den ersten $12$ Sekunden nach dem Start
durch die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x) =\frac1{576}\cdot x^4 −\frac1{18}\cdot x^3 +\frac{1}{2}\cdot x^2$ beschrieben.
Dabei ist $x$ die seit dem Start vergangene Zeit in Sekunden und $f (x)$ bzw. $h (x)$ die
Geschwindigkeit in Meter pro Sekunde $(\frac{\text{m}}{\text{s}})$ .
Berechnen Sie die Geschwindigkeit von Radfahrer $F$ drei Sekunden nach dem Start
sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von $8\;\frac{\text{m}}{\text{s}}$ erreicht. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Berechne $f (3)$ :
$f (3) = 3,483$
Die Geschwindigkeit beträgt etwa $3{,}5 \;\frac{\text{m}}{\text{s}}$ .
Löse $(f (x) = 8)$ :
Die Gleichung hat im betrachteten Zeitraum die Lösung $x \approx5{,}82$ , d. h. die
Geschwindigkeit wird etwa $5,8$ Sekunden nach dem Start erreicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne $f (3)$ .
Teil 2
Löse $(f (x) = 8)$ .
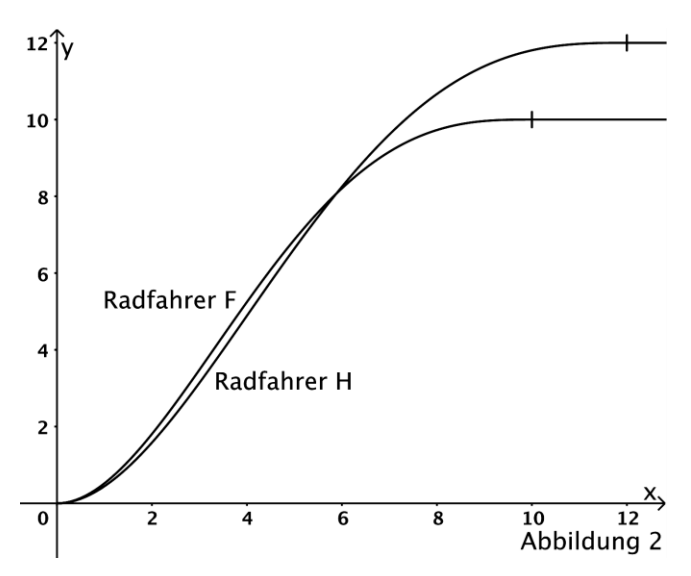
Nach den ersten $12$ Sekunden fährt Radfahrer $H$ mit konstanter Geschwindigkeit.
Geben Sie diese konstante Geschwindigkeit an.
Zeigen Sie durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der
Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Gib diese konstante Geschwindigkeit an
Berechne $h (12)$ :
$h (12) = 12$
Die konstante Geschwindigkeit beträgt $12\;\frac{\text{m}}{\text{s}}$ .
Zeige durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist
Berechne $h^{'} (12)$ :
$h^{'} (12) = 0$ , d.h. die Tangente hat an der Stelle $x = 0$ die Steigung null (waagrechte Tangente).
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne $h (12)$ .
Teil 2
Berechne $h^{'} (12)$ .
Nach dem Start gibt es genau einen Zeitpunkt, zu dem die Geschwindigkeiten beider
Radfahrer gleich groß sind. Im Modell wird dieser Zeitpunkt mit $x_{s}$ bezeichnet.
Berechnen Sie $x_{s}$ . [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Berechne $x_{s}$
Löse $(f (x) = h (x))$ :
Für $0 < x < 10$ hat die Gleichung die Lösung $x_s =\dfrac{880−20}{91}\cdot \sqrt{298}\approx5{,}88$ .
Der Zeitpunkt, zu dem die Geschwindigkeiten beider Radfahrer gleich groß sind, ist etwa $5,88$ Sekunden nach dem Start.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse $($ $f (x) = h (x)$ $)$ .
Es gibt genau einen Zeitpunkt in den ersten $10$ Sekunden nach dem Start, zu dem einer
der beiden Radfahrer den anderen überholt.
Berechnen Sie, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die
Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt.
[5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt
Der zurückgelegte Weg muss beim Überholen für beide Radfahrer gleich groß sein. d.h. das $\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x$ muss gleich null sein (gleicher zurückgelegter Weg).
$\text{Löse}\left(\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x=0,z\right)$
Für $0 < z < 10$ erhält man die Lösung $z_1=\dfrac{1100-20\cdot\sqrt{295}}{91}$ .
Berechne die prozentuale Änderung:
Es ist $\dfrac{h(z_1)-f(z_1)}{f(z_1)}\approx 0{,}11=11\;\%$
Um $11 %$ Prozent übersteigt die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der zurückgelegte Weg muss beim Überholen für beide Radfahrer gleich groß sein, d.h. das $\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x$ muss gleich null sein (gleicher zurückgelegter Weg).
Man erhält für $0 < z < 10$ die Lösung $z_{1}$ .
Berechne mit dem Wert $z_{1}$ die prozentuale Änderung.

2

Aufgabe 1B

Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in $\mathbb{R}$ definierten Funktion $𝑓$ mit $𝑓(𝑡) = 25 − 20𝑒^{−0{,}014⋅𝑡}$ modellhaft beschreiben. Dabei ist $t$ die Zeit in Minuten, die seit der Entnahme aus dem Kühlschrank vergangen ist, und $f (t)$ die Wassertemperatur in $^\circ C$ . Die Raumtemperatur beträgt konstant $25^\circ C$ .

Geben Sie die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.
Bestimmen Sie den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.
Berechne $f (0)$ :
$f (0) = 25 - 20 = 5$
Die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank beträgt $5^\circ C$ .
Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt
$\text{Löse}(f(t)=12)$ , man erhält die Lösung $t\approx30{,}8$ .
Das Wasser hat rund $31$ Minuten nach der Entnahme eine Temperatur von $12^\circ C$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne $f (0)$ .
Teil 2
$\text{Löse}(f(t)=12)$ .
Berechnen Sie die Werte der folgenden Terme und interpretieren Sie diese im Sachzusammenhang: [6 BE]
1. $f^{'} (30)$
2. $\dfrac{𝑓(30)−𝑓(0)}{30−0}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Die mittlere Änderungsrate – Einführung der Ableitung
Berechne die Werte der folgenden Terme und interpretiere diese im Sachzusammenhang
$\mathrm{(I)}\;$ : $f'(30) \approx 0{,}18$
$f^{'} (30)$ beschreibt die momentane Änderungsrate der Wassertemperatur $30$ Minuten nach Entnahme in Grad pro Minute.
$\mathrm{(II)}\;$ : $\dfrac{f(30)−f(0)}{30−0}\approx0{,}23$

$\dfrac{f(30)−f(0)}{30−0}$ beschreibt die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten in Grad pro Minute.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $f^{'} (30)$ . Die erste Ableitung entspricht der momentanen Änderungsrate.
Berechne $\dfrac{f(30)−f(0)}{30−0}$ . Sekantensteigung oder mittlere Änderungsrate.
Gegeben ist die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x) = (1 − x^2) \cdot e^x$ .
Der Graph von $h$ wird mit $G_{h}$ bezeichnet.
Begründen Sie anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: e-Funktion
Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist
Die Funktion hat die beiden Nullstellen $x_{1} = - 1$ und $x_{2} = 1$ .
Betrachte den Funktionsterm: $(1 − x^2)\cdot e^x$
$e^{x}$ ist für alle $x$ größer null.
Der Term $(1 - x^{2})$ ist für $- 1 < x < + 1$ ebenfalls größer null, sodass das Produkt aus den beiden Termen $e^{x}$ und $(1 - x^{2})$ ebenfalls größer null ist.
(Für x-Werte außerhalb des Intervalls $] - 1; 1 [$ ist der Term $(1 - x^{2})$ kleiner null.)
Damit ist $h (x)$ nur für $- 1 < x < 1$ positiv.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Nullstellen der Funktion $f$ .
Betrachte die beiden Terme $(1 - x^{2})$ und $e^{x}$ und entscheide, für welche x-Werte die Terme größer oder kleiner null sind.
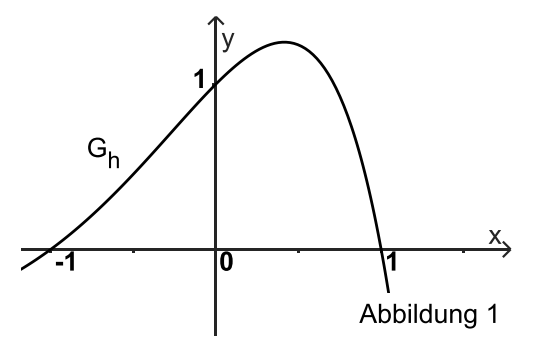
Die Gerade $u$ ist die Tangente an $G_{h}$ im Punkt $(0 ∣ 1)$ . Es gibt genau eine Tangente $v$ an $G_{h}$ , die zu $u$ senkrecht ist. Geben Sie die notwendigen Schritte zur Berechnung einer Gleichung von $v$ an und erläutern Sie diese. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Gib die notwendigen Schritte zur Berechnung einer Gleichung von $v$ an und erläutere diese
Die Gerade $u$ ist die Tangente an $G_{h}$ im Punkt $(0 ∣ 1)$ $\;\Rightarrow\;m_u=h'(0)$
Es gibt eine Tangente $v$ an $G_{h}$ , die zu $u$ senkrecht ist $\;\Rightarrow\;m_u\cdot m_v=-1$
Steigung von $v: m_v=-\dfrac{1}{m_u}=-\dfrac{1}{h'(0)}$
Lösen der Gleichung $h'(x)= − \dfrac{1}{h'(0)}$ zur Bestimmung der x-Koordinate $x_{Q}$ des Berührpunkts $Q$ von $G_{h}$ und $v$ .
Bestimmung der y-Koordinate $y_{Q}$ von $Q$ : $y_{Q} = h (x_{Q})$
Bestimmung des y-Achsenabschnitts von $v$ mithilfe der Steigung von $v$ und der Koordinaten von $Q$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Steigung von $m_v=-\dfrac{1}{m_u}=-\dfrac{1}{h'(0)}$
Löse $h'(x)= − \dfrac{1}{h'(0)}$ zur Bestimmung der x-Koordinate $x_{Q}$ des Berührpunkts $Q$ von $G_{h}$ und $v$ .
Berechne $y_{Q} = h (x_{Q})$
Bestimmung des y-Achsenabschnitts von $v$ mithilfe der Steigung von $v$ und der Koordinaten von $Q$ .
Berechnen Sie die Wendestellen von $h$ . In einem der Wendepunkte von $G_{h}$ ist die Steigung von $G_{h}$ maximal. Berechnen Sie den Wert der maximalen Steigung. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Berechne die Wendestellen von $h$
$\text{Löse}(h''(x) = 0)$ $\;\Rightarrow\;$ $x_1 = −2 − \sqrt{3}$ und $x_2 = −2 + \sqrt{3}$ .
Es gibt zwei Wendestellen $x_{1}$ und $x_{2}$ .
Berechne den Wert der maximalen Steigung
Da $h^{'''} (x_{1}) > 0$ und $h^{'''} (x_{2}) < 0$ , ist $x_{2}$ die x-Koordinate des Punktes, in dem die
Steigung von $G_{h}$ maximal ist.
Anmerkung: $h^{'''} (x_{2})$ ist die 2. Ableitung von $h^{'} (x)$ und wenn die 2. Ableitung kleiner null ist, handelt es sich um ein Maximum.
Berechne $h^{'} (x_{2})$ :
Ergebnis berechnet mit dem CAS-Rechner von Geogebra
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
$\text{Löse}(h''(x) = 0)\;\Rightarrow\;x_1$ und $x_{2}$
Teil 2
Betrachte $h^{'''} (x_{1})$ und $h^{'''} (x_{2})$ . Ist einer dieser beiden Werte kleiner null, dann gibt es an dieser Stelle die maximale Steigung.
Für $0 < 𝑤 < 1$ wird das Dreieck mit den Eckpunkten $(0 ∣ 0)$ , $(w ∣ 0)$ und $(w ∣ h (w))$ betrachtet. Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal.
Berechnen Sie den maximalen Flächeninhalt. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal
Skizze:
Es ist $A(w)=\dfrac{1}{2}\cdot w\cdot h(w)=\dfrac{1}{2}\cdot w\cdot (1 − w^2) \cdot e^w$
$\text{Löse}(A'(w) = 0)\;\Rightarrow\;$ im Bereich $0 < w < 1$ gibt es die Lösung $w\approx 0{,}68$ .
Der Flächeninhalt des Dreiecks ist maximal für $w\approx 0{,}68$ .
Berechne den maximalen Flächeninhalt
Berechne $A (0,68)$ :
$A(0{,}68)\approx0{,}36$
Der maximale Flächeninhalt beträgt rund $0{,}36\;\text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Es ist $A(w)=\dfrac{1}{2}\cdot w\cdot h(w)$ . $\text{Löse}(A'(w) = 0)\;\Rightarrow\; w_1$
Teil 2
Berechne $A (w_{1})$ .
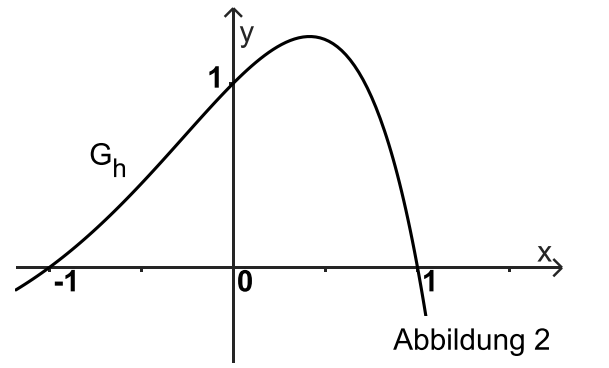
$G_{h}$ schließt mit der x-Achse eine Fläche $A$ ein.
Es gibt genau einen Punkt $P$ auf $G_{h}$ mit positiver x-Koordinate, sodass die Gerade durch die Punkte $O (0 ∣ 0)$ und $P$ die Fläche $A$ in zwei Flächenstücke gleichen Inhalts teilt.
Geben Sie eine Gleichung an, mit der die
x-Koordinate von $P$ bestimmt werden kann. Veranschaulichen Sie den Aufbau der Gleichung in Abbildung 2. [7 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Gib eine Gleichung an, mit der die x-Koordinate von $P$ bestimmt werden kann
Für die Koordinate $x_{P}$ des Punktes $P$ gilt:
Die Hälfte der Fläche, die $G_{h}$ mit der x-Achse einschließt, ist so groß wie die Summe der beiden Flächen $\textcolor{ff6600}{A_1}$ und $\textcolor{660099}{A_2}$ .
$\dfrac{1}{2}\cdot\underbrace{\displaystyle\int_{-1}^1h(x)\;\mathrm{d}x}_{A{\text{gesamt}}}=\textcolor{ff6600}{ \underbrace{\dfrac{1}{2}\cdot x_P\cdot h(x_P)}_{A_1}}+\textcolor{660099}{\underbrace{\displaystyle\int_{x_P}^1h(x)\;\mathrm{d}x}_{A_2}}$

Veranschauliche den Aufbau der Gleichung in Abbildung 2
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Zeichne einen Punkt $P$ auf $G_{h}$ mit positiver x-Koordinate ein. $x_{P}$ ist seine x-Koordinate.
Die Hälfte der Fläche, die $G_{h}$ mit der x-Achse einschließt, ist so groß wie die Summe der Dreiecksfläche $A_{Ox_PP}$ und der Fläche unter $G_{h}$ von $x_{P}$ bis $1$ .
Teil 2
Markiere die unter Teil 1 angegebenen Flächen in der Abbildung 2.

3

Aufgabe 2A

Bei einer Studie über das Kaufverhalten von Kunden eines Baumarktes werden ausschließlich Kunden betrachtet, die sich registrieren ließen. Aus der Gruppe dieser Kunden wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

$T$ : „Die Person ist sogenannter Treuekunde, d. h. sie ist bereits länger als fünf Jahre ein registrierter Kunde des Baumarktes.“
$M$ : „Die Person ist sogenannter Morgenkunde, d. h. sie kauft überwiegend vor $10$ Uhr ein.“

Bei dieser Studie wurde festgestellt, dass $60 %$ aller Kunden Treuekunden und $20 %$ aller

Kunden Morgenkunden sind.

Es gilt $P(\overline{T} \cap M)=0{,}05$ . Interpretieren Sie diese Gleichung im Sachzusammenhang. [2 BE]
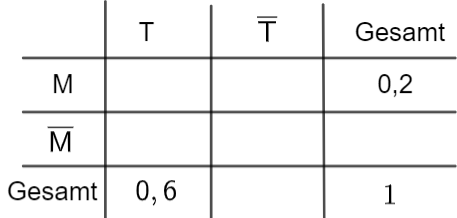
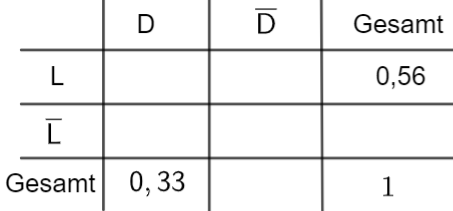
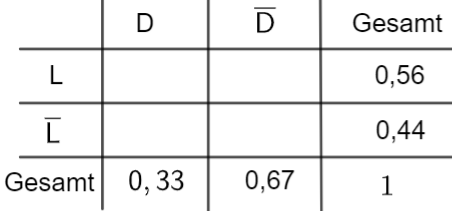
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Interpretiere die Gleichung $P(\overline{T} \cap M)=0{,}05$ im Sachzusammenhang
$\overline{T}$ : Die Person ist kein sogenannter Treuekunde.
$M$ : Die Person ist ein sogenannter Morgenkunde.
Für $P(\overline{T} \cap M)=0{,}05$ gilt dann:
Die Wahrscheinlichkeit dafür, dass die ausgewählte Person ein Morgenkunde und kein Treuekunde ist, beträgt $5 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\overline{T}$ : Die Person ist kein sogenannter Treuekunde und $M$ : Die Person ist ein sogenannter Morgenkunde.
Was ist dann $P(\overline{T} \cap M)=0{,}05$ ?
Stellen Sie den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar
Laut Aufgabenstellung sind $60 %$ aller Kunden Treuekunden und $20 %$ aller
Kunden Morgenkunden.
Mit diesen beiden Angaben beginnt die Vierfeldertafel:
Zunächst können durch Differenzbildung zwei weitere Felder ausgefüllt werden:
Aus Aufgabe a) folgt: $P(\overline{T} \cap M)=0{,}05$ . Dieser Wert wird eingetragen.
Dann ist $P(T\cap M)=0{,}2-0{,}05=0{,}15$ und $P(T \cap \overline{M})=0{,}6-0{,}15=0{,}45$ .
Der letzte Wert ist dann $P(\overline{T} \cap \overline{M})=0{,}4-0{,}05=0{,}35$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$60 %$ aller Kunden sind Treuekunden und $20 %$ aller Kunden sind Morgenkunden. Trage diese Werte ein und ergänze die Differenzwerte zu $1$ .
Aus Aufgabe a) kann ein weiter Wert in die Tafel eingetragen werden. Die restlichen Werte erfolgen durch Differenzbildung.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass die ausgewählte Person entweder ein
Treuekunde oder ein Morgenkunde ist. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Ermittele die Wahrscheinlichkeit dafür, dass die ausgewählte Person entweder ein Treuekunde oder ein Morgenkunde ist
Entnimm die Wahrscheinlichkeiten der Vierfeldertafel aus Aufgabe b).
Gesucht ist dann die Wahrscheinlichkeit:
$P(T\cap \overline{M}) + P(\overline{T} \cap M)= 0{,}45 + 0{,}05 = 0{,}5=50\;\%$ .
Die Wahrscheinlichkeit dafür, dass die ausgewählte Person entweder ein Treuekunde oder ein Morgenkunde ist, beträgt $50 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gesucht ist die Wahrscheinlichkeit $P(T\cap \overline{M}) + P(\overline{T} \cap M)$ .
Entnimm die entsprechenden Werte der Vierfeldertafel.
Untersuchen Sie, ob die Ereignisse $T$ und $M$ stochastisch unabhängig sind. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
Untersuche, ob die Ereignisse $T$ und $M$ stochastisch unabhängig sind
Zwei Ereignisse sind stochastisch unabhängig, falls gilt: $P_{T} (M) = P (M)$
Es ist $P_T(M)=\dfrac{P(T\cap M)}{P(T)}=\dfrac{0{,}15}{0{,}6}=0{,}25$ und $P (M) = 0,2$ .
Aufgrund der Ungleichheit der beiden Wahrscheinlichkeiten sind $T$ und $M$ nicht
stochastisch unabhängig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche, ob gilt $P_{T} (M) = P (M)$ ?
Im Baumarkt wird ein Gewinnspiel mit einem Glücksrad angeboten. Das Glücksrad besteht aus gleich großen Sektoren, die jeweils entweder mit der Zahl $5$ oder mit der Zahl $2$ beschriftet sind.
Bei diesem Gewinnspiel dreht eine Person zweimal das Glücksrad und kann
dabei einen Rabatt gewinnen. Das Produkt der beiden erzielten Zahlen entspricht dem
Rabatt in Prozent.
Die Wahrscheinlichkeit dafür, in beiden Drehungen die Zahl 5 zu erzielen, beträgt $\frac1{36}$ und die Wahrscheinlichkeit dafür, den kleinstmöglichen Rabatt zu erzielen, beträgt $\frac{25}{36}$ .
Stellen Sie das dem Gewinnspiel zugrundeliegende Zufallsexperiment in einem
beschrifteten Baumdiagramm dar. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Stelle das dem Gewinnspiel zugrundeliegende Zufallsexperiment in einem beschrifteten Baumdiagramm dar
Es gilt: $P(55)=\dfrac{1}{36}\;\Rightarrow\;P(5)=\dfrac{1}{6}$
Den kleinstmöglichen Rabatt erhält man, wenn zweimal die $2$ erzielt wird:
$P(22)=\dfrac{25}{36}\;\Rightarrow\;P(2)=\dfrac{5}{6}$
Damit kann das Baumdiagramm erstellt werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es sind $P (55)$ und $P (22)$ gegeben. Damit können $P (5)$ und $P (2)$ berechnet werden.
Dann kann das Baumdiagramm erstellt werden.
Betrachtet werden sieben Personen, die nacheinander jeweils einmal am Gewinnspiel
teilnehmen.
Berechnen Sie die Wahrscheinlichkeit dafür, dass dabei genau viermal der kleinstmögliche Rabatt erzielt wird und dies bei vier Personen unmittelbar hintereinander. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Berechne die Wahrscheinlichkeit dafür, dass dabei genau viermal der kleinstmögliche Rabatt erzielt wird und dies bei vier Personen unmittelbar hintereinander
In der Skizze sind die Möglichkeiten dargestellt. Die schwarzen Felder stehen für irgendeinen Rabatt, nur nicht für den kleinstmöglichen Rabatt.
Die mit $2$ beschrifteten Felder stehen für den kleinstmöglichen Rabatt.
Es gibt also $4$ solche Anordnungen.
$P(\text{"irgendeinen Rabatt"})=1-P(\text{"kleinstmöglicher Rabatt"})=1-\dfrac{25}{36}=\dfrac{11}{36}$
$P(\text{"kleinstmöglicher Rabatt"})=\dfrac{25}{26}$
$P(\text{"irgendeinen Rabatt"})$ tritt 3-mal auf $\;\Rightarrow\;p=\left(\dfrac{11}{36}\right)^3$
$P(\text{"kleinstmöglicher Rabatt"})$ tritt 4-mal auf $\;\Rightarrow\;p= \left(\dfrac{25}{26}\right)^4$
Da es $4$ Anordnungen gibt, gilt für die Wahrscheinlichkeit:
$p=4\cdot\left(\dfrac{25}{36}\right)^4\cdot\left(\dfrac{11}{36}\right)^3\approx0{,}027$
Die Wahrscheinlichkeit dafür, dass dabei genau viermal der kleinstmögliche Rabatt erzielt wird und dies bei vier Personen unmittelbar hintereinander, beträgt rund $2,7 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle eine Reihe mit $7$ Kästchen und kreuze $4$ zusammenhängende Kästchen von links an.
Schiebe dann in der nächsten Reihe die $4$ Kästchen mit den Kreuzen um $1$ Kästchen weiter.
Wie viele Reihen gibt es insgesamt, bis die $4$ Kästchen mit den Kreuzen am Ende der Reihe angekommen sind?
Berechne die Wahrscheinlichkeit für $P(\text{"irgendeinen Rabatt"})$ , die $3$ -mal auftritt und die Wahrscheinlichkeit $P(\text{"kleinstmöglicher Rabatt"})$ , die $4$ -mal auftritt.

Die Geschäftsführung des Baumarkts setzt ein anderes Glücksrad ein, das ebenfalls

zweimal gedreht wird. Dieses hat ebenfalls mehrere Sektoren, von denen einige mit der

Zahl $5$ und die anderen mit der Zahl $2$ beschriftet sind.

Durch Änderung der Größen der Sektoren kann jedoch die Wahrscheinlichkeit $q$ dafür, beim einmaligen Drehen die Zahl $5$ zu erzielen, variiert werden. Der Rabatt, der einer Person beim nächsten Einkauf gewährt wird, wird auf gleiche Weise wie bisher ermittelt.

Berechnen Sie die Wahrscheinlichkeit $q$ , wenn beim Glücksspiel mit dem Glücksrad auf

lange Sicht im Mittel ein Rabatt von $9 %$ erzielt werden soll. [4 BE]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Berechne die Wahrscheinlichkeit $q$ , wenn beim Glücksspiel mit dem Glücksrad auf lange Sicht im Mittel ein Rabatt von $9 %$ erzielt werden soll

Beim einmaligen Drehen die Zahl $5$ zu erzielen hat die Wahrscheinlichkeit $q$ .

Beim einmaligen Drehen die Zahl $2$ zu erzielen, hat dann die Wahrscheinlichkeit $1 - q$ .

Ergebnis	$55$	$52$	$25$	$22$
Rabatt in $%$	$25 %$	$10 %$	$10 %$	$4 %$
Wahrschein-lichkeit	$q\cdot q$	$q\cdot(1-q)$ $~~~~~~~~~~~~~~~~~~$	$q\cdot(1-q)$ $~~~~~~~~~~~~~~~~~~$	$(1 - q)^{2}$ $~~~~~~~~~~~~~~~~~~$

Man erhält dann als Erwartungswert:

$E=0{,}25\cdot q^2+2\cdot0{,}1\cdot q\cdot(1-q)+0{,}04\cdot(1-q)^2$

Da im Mittel ein Rabatt von $9 %$ erzielt werden soll, folgt:

$0{,}09=0{,}25\cdot q^2+2\cdot0{,}1\cdot q\cdot(1-q)+0{,}04\cdot(1-q)^2$

$\text{Löse}(0{,}09=0{,}25\cdot q^2+2\cdot0{,}1\cdot q\cdot(1-q)+0{,}04\cdot(1-q)^2,q)$

$=\{q=-\dfrac{5}{3}; q=\dfrac{1}{3}\}$

Die Gleichung liefert im Sachkontext die Lösung $q=\dfrac{1}{3}$ .

Wenn beim Glücksspiel mit dem Glücksrad auf lange Sicht im Mittel ein Rabatt von $9 %$ erzielt werden soll, muss die Wahrscheinlichkeit, ⁣die Zahl $5$ zu erzielen, $\dfrac{1}{3}$ betragen.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

4

Aufgabe 2B

Eine umfassende Studie zu den Arbeits- und Lebensbedingungen von Studierenden einer

Universität ergab, dass $56 %$ der Studierenden einen Laptop und $33 %$ einen Desktop-PC

besitzen. $72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte.

Unter den Studierenden der Universität wird eine Person zufällig ausgewählt und zum Besitz von digitalen Endgeräten befragt. Folgende Ereignisse werden betrachtet:

$L$ : „Die Person besitzt einen Laptop.“
$D$ : „Die Person besitzt einen Desktop-PC.“

Zeigen Sie, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt, und geben Sie das zugrundeliegende Ereignis im Sachzusammenhang an. [3 BE]
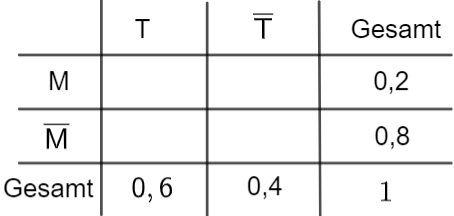
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Zeige, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt
$72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte.
$\Rightarrow\; P(L\cap D)+P(L\cap \overline{D})+P( \overline{L}\cap D)=0{,}72$
$\Rightarrow\;P(\overline{L} \cap \overline{D})=1-\left(P(L\cap D)+P(L\cap \overline{D})+P( \overline{L}\cap D)\right)=1-0{,}72=0{,}28$
Gib das zugrundeliegende Ereignis im Sachzusammenhang an
Ereignis: Die ausgewählte Person besitzt weder einen Laptop noch einen
Desktop-PC.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
$72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte. Gib dazu das Gegenereignis an.
Teil 2
Was bedeuten $\overline{L}$ und $\overline{D}$ . Wie lautet das zugehörige Ereignis?
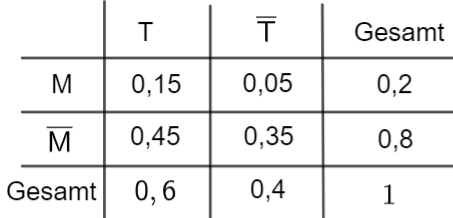
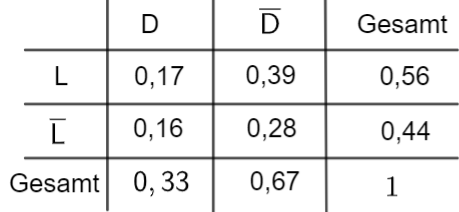
Stellen Sie den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.
Geben Sie die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar
einen Laptop, jedoch keinen Desktop-PC besitzt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar
Laut Aufgabenstellung haben $56 %$ der Studierenden einen Laptop und $33 %$ besitzen einen Desktop-PC.
Mit diesen beiden Angaben beginnt die Vierfeldertafel:
Zunächst können durch Differenzbildung zwei weitere Felder ausgefüllt werden:
Aus Aufgabe a) folgt: $P(\overline{L} \cap \overline{D})=0{,}28$ . Dieser Wert wird eingetragen.
Dann ist $P({L} \cap \overline{D})=0{,}67-0{,}28=0{,}39$ und $P(\overline{L} \cap {D})=0{,}44-0{,}28=0{,}16$ .
Der letzte Wert ist dann $P({L} \cap {D})=0{,}33-0{,}16=0{,}17$ .
Die vollständige Vierfeldertafel sieht dann so aus:
Gib die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar einen Laptop, jedoch keinen Desktop-PC besitzt
Gesucht ist hier die Wahrscheinlichkeit $P(L\cap \overline{D})$ .
Aus der Vierfeldertafel entnimmt man: $P(L \cap \overline{D})=0{,}39$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Laut Aufgabenstellung haben $56 %$ der Studierenden einen Laptop und $33 %$ besitzen einen Desktop-PC. Trage diese Werte ein und ergänze die Differenzwerte zu $1$ .
Aus Aufgabe a) kann ein weiterer Wert in die Tafel eingetragen werden. Die restlichen Werte erfolgen durch Differenzbildung.
Teil 2
Gesucht ist hier die Wahrscheinlichkeit $P(L\cap \overline{D})$ .
Nun wird unter allen Befragten, die einen Desktop-PC haben, eine Person zufällig
ausgewählt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Berechne die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt
Gesucht ist $P_{D} (L)$ :
Mit den Werten aus der Vierfeldertafel folgt:
$P_D(L)=\dfrac{P(L\cap D)}{P(D)}=\dfrac{0{,}17}{0{,}33}\approx0{,}52$
Die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt, beträgt rund $52 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne mit den Werten aus der Vierfeldertafel $P_D(L)=\dfrac{P(L\cap D}{P(D)}$ .
In derselben Studie wurde auch festgestellt, dass $68 %$ der Besitzer von Laptops und
Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen.
Unter den Besitzern dieser Endgeräte werden $900$ Personen zufällig ausgewählt. Die
Zufallsgröße $X$ beschreibt die Anzahl derjenigen unter diesen $900$ Personen, die versuchen, ein Software-Problem selbstständig zu lösen. Dabei wird $X$ als binomialverteilt angenommen.
Berechnen Sie die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen
bei einem Software-Problem versuchen, dieses selbstständig zu lösen. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Berechne die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen
$70 %$ dieser $n = 900$ Personen sind $630$ Personen.
Gegeben ist weiterhin, dass $68 %$ der Besitzer von Laptops und
Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen $\;\Rightarrow\;p=0{,}68$
Gesucht ist die Wahrscheinlichkeit: $P(X\leq 630)=\text{binomCdf}(900;0{,}68;0;630)\approx0{,}9075$
Die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen, beträgt rund $91 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $70 %$ von $n = 900$ Personen.
Gegeben ist, dass $68 %$ der Besitzer von Laptops und Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen.
Berechne $P(X\leq 70\;\%\text{ von}\; 900)$ .
Berechnen Sie den Erwartungswert $μ \mu$ von $X$ und ermitteln Sie die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Berechne den Erwartungswert $μ \mu$ von $X$
Es ist $\mu=n\cdot p=900\cdot 0{,}68=612$
Der Erwartungswert von $X$ beträgt $612$ .
Ermittele die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt
Gefordert ist: $P(\mu − k ≤ X ≤ \mu) ≥ 0{,}3$
$\Rightarrow\;P(612− k ≤ X ≤ 612) ≥ 0{,}3$
Man findet:
$P(600 ≤ X ≤ 612) \approx 0{,}3269 > 0{,}3$
$P(601 ≤ X ≤ 612) \approx 0{,}3072>0{,}3$
$P(602 ≤ X ≤ 612) \approx 0{,}2866<0{,}3$
Also ist hier die richtige Lösung: $P(612− 11 ≤ X ≤ 612)\approx0{,}3072>0{,}3\;\Rightarrow\;k=11$
Die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt, ist $k = 11$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Es ist $\mu=n\cdot p$ .
Teil 2
Gefordert ist: $P(\mu − k ≤ X ≤ \mu) ≥ 0{,}3$
Setze $μ \mu$ in die Ungleichung ein und probiere einige Werte für $k$ aus, sodass die Ungleichung gerade erfüllt wird.
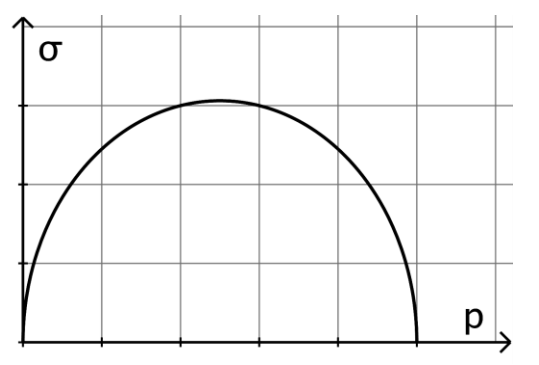
Für binomialverteilte Zufallsgrößen mit den Parametern $n = 15000$ und $p$ ist in der Abbildung die Standardabweichung $\sigma$ in Abhängigkeit von $p$ dargestellt.
Ergänzen Sie im dargestellten Koordinatensystem die
Skalierungen der Achsen und
erläutern Sie Ihr Vorgehen. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Ergänze im dargestellten Koordinatensystem die Skalierungen der Achsen und erläutere Dein Vorgehen
Es gilt: $0\leq p\leq 1$
Deshalb muss die rechte Grenze des Graphens auf der p-Achse $1$ sein.
(Ein Kästchen auf der p-Achse entspricht dann $0,2$ .)
Bei $p = 0,4$ (in der Skizze eingetragen) kann der $\sigma$ -Wert genau bestimmt werden.
Es ist $\sigma=\sqrt{n\cdot p\cdot(1-p)}$ .
Mit $n = 15000$ und $p = 0,4$ folgt dann:
$\sigma=\sqrt{15000\cdot 0{,}4\cdot 0{,}6}=60$
(Ein Kästchen auf der $\sigma$ -Achse entspricht dann $20$ .)
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es gilt: $0\leq p\leq 1$
Die rechte Grenze des Graphens ist damit bestimmt.
Bei einem bestimmten p-Wert kann der $\sigma$ -Wert genau bestimmt werden.
Berechne $\sigma=\sqrt{n\cdot p\cdot(1-p)}$ .

5

Aufgabe 3A

Abbildung 1 zeigt die Pyramide $A B C D S$ mit $A (0 ∣ 0 ∣ 0), B (2 ∣ 0 ∣ 0), C (2 ∣ 2 ∣ 0), D (0 ∣ 4 ∣ 0)$ und $S (0 ∣ 0 ∣ 3,5) .$

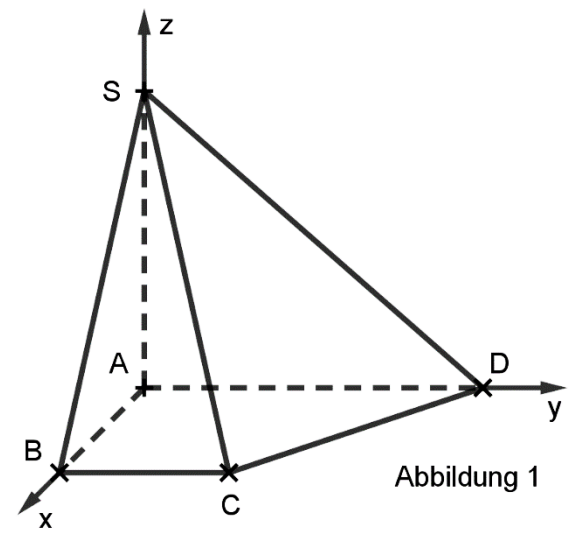
Begründen Sie, dass die Grundfläche der Pyramide ein Trapez ist.
Berechnen Sie das Volumen der Pyramide. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Begründe, dass die Grundfläche der Pyramide ein Trapez ist
Berechne die Vektoren $\overrightarrow{BC}$ und $\overrightarrow{AD}$ :
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=\begin{pmatrix}2\\2\\0\end{pmatrix}-\begin{pmatrix}2\\0\\0\end{pmatrix}=\begin{pmatrix}0\\2\\0\end{pmatrix}$
$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}=\begin{pmatrix}0\\4\\0\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}=\begin{pmatrix}0\\4\\0\end{pmatrix}$
$\Rightarrow\; \overrightarrow{AD}\parallel \overrightarrow{BC}$
Das Rechteck ist ein Trapez.
Berechne das Volumen der Pyramide
$V=\dfrac{1}{3}\cdot G \cdot h_P$
Die Grundfläche $G$ ist ein Trapez: $G_{\text{Trapez}}=\frac{\left(a+c\right)}2\cdot h_T=\dfrac{2+4}{2}\cdot 2=6$
$V=\dfrac{1}{3}\cdot G \cdot h_P=\dfrac{1}{3}\cdot 6\cdot 3{,}5=7$
( $z = 3,5$ ist die z-Koordinate von $S$ und ist die Höhe der Pyramide.)
Das Volumen der Pyramide beträgt $7\;\text{VE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Vergleiche die Vektoren $\overrightarrow{BC}$ und $\overrightarrow{AD}$ .
Teil 2
Berechne $V=\dfrac{1}{3}\cdot G \cdot h_P$
Zeigen Sie, dass das Dreieck $C D S$ im Punkt $C$ rechtwinklig ist. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Zeige, dass das Dreieck $C D S$ im Punkt $C$ rechtwinklig ist
Berechne die Vektoren $\overrightarrow{CD}$ und $\overrightarrow{CS}$ :
$\overrightarrow{CD}=\overrightarrow{OD}-\overrightarrow{OC}=\begin{pmatrix}0\\4\\0\end{pmatrix}-\begin{pmatrix}2\\2\\0\end{pmatrix}=\begin{pmatrix}-2\\2\\0\end{pmatrix}$
$\overrightarrow{CS}=\overrightarrow{OS}-\overrightarrow{OC}=\begin{pmatrix}0\\0\\3{,}5\end{pmatrix}-\begin{pmatrix}2\\2\\0\end{pmatrix}=\begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}$
Berechne das Skalarprodukt der beiden Vektoren:
$\overrightarrow{CD}\circ \overrightarrow{CS}=\begin{pmatrix}-2\\2\\0\end{pmatrix}\circ \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}=(-2)\cdot(-2)+2\cdot(-2)+0\cdot 3{,}5=4-4+0=0$
Demnach befindet sich bei $C$ ein rechter Winkel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne das Skalarprodukt der Vektoren $\overrightarrow{CD}$ und $\overrightarrow{CS}$ .
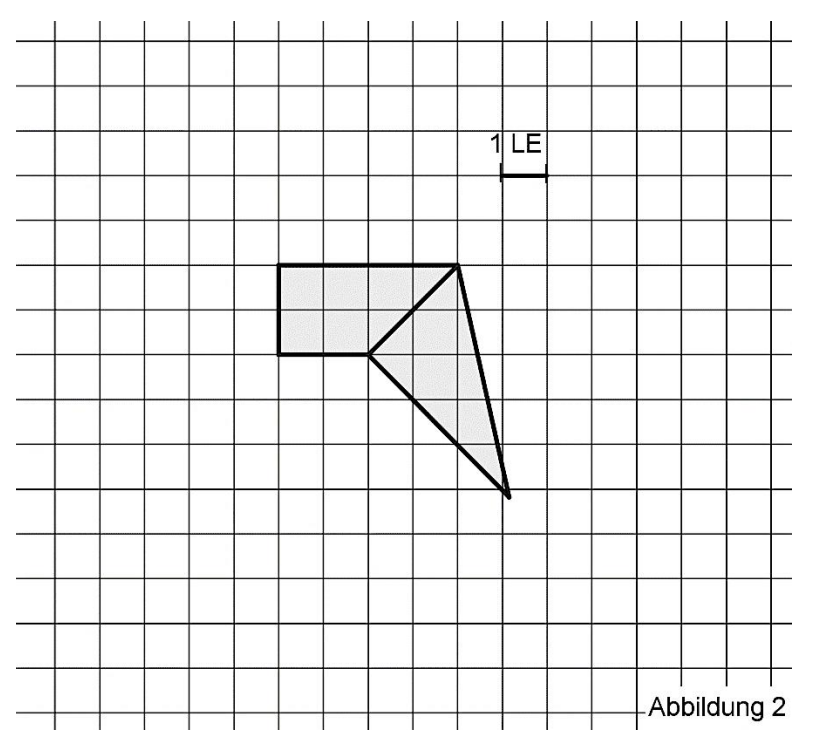
In Abbildung 2 ist ein Teil eines Netzes der Pyramide $A B C D S$ dargestellt.
Ergänzen Sie Abbildung 2 so, dass ein
vollständiges Netz der Pyramide
$A B C D S$ dargestellt ist. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
Ergänze Abbildung 2 so, dass ein vollständiges Netz der Pyramide $A B C D S$ dargestellt ist
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne das Pyramidennetz. Orientiere Dich an der vorgegebenen Seitenfläche $C D S$ und berücksichtige die Pyramidenhöhe von $3,5$ .
Untersuchen Sie, ob der Punkt $P (4 ∣ - 8 ∣ 7)$ in der Ebene liegt, in der die Seitenfläche $C D S$ liegt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung Punkt-Ebene (Inzidenz)
Untersuche, ob der Punkt $P (4 ∣ - 8 ∣ 7)$ in der Ebene liegt, in der die Seitenfläche $C D S$ liegt
Erstelle die Ebenengleichung durch die Punkte $C, D$ und $S$ .
$E:\;\vec x=\overrightarrow{OC}+r\cdot \left(\overrightarrow{OD} -\overrightarrow{OC}\right) +s\cdot \left(\overrightarrow{OS}-\overrightarrow{OC}\right)$
$E:\vec x=\begin{pmatrix}2\\2\\0\end{pmatrix}+r\cdot \left(\begin{pmatrix}0\\4\\0\end{pmatrix}-\begin{pmatrix}2\\2\\0\end{pmatrix}\right)+s\cdot \left(\begin{pmatrix}0\\0\\3{,}5\end{pmatrix}-\begin{pmatrix}2\\2\\0\end{pmatrix}\right)$
$E:\vec x=\begin{pmatrix}2\\2\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}+s\cdot \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}$
Führe eine Punktprobe durch:
$\begin{pmatrix}4\\-8\\7\end{pmatrix}=\begin{pmatrix}2\\2\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}+s\cdot \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}\;\Rightarrow\;$
$\begin{pmatrix}2\\-10\\7\end{pmatrix}=r\cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}+s\cdot \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}$
Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.
$\mathrm{(III)}\quad 7=3{,}5\cdot s\;\Rightarrow\;s=2$
$s = 2$ eingesetzt in Gleichung $\mathrm{(I)}\;\Rightarrow\; 2=-2\cdot r-4$
$\Rightarrow\;6=-2\cdot r\;\Rightarrow\;r=-3$
Kontrolle in Gleichung $\mathrm{(II)}$ :
$-10=(-3)\cdot2+2\cdot (-2)\;\Rightarrow\;-10=-10\;\checkmark$
Der Punkt $P (4 ∣ - 8 ∣ 7)$ liegt in der Ebene, in der die Seitenfläche $C D S$ liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle die Ebenengleichung durch die Punkte $C, D$ und $S$ .
Führe eine Punktprobe durch.
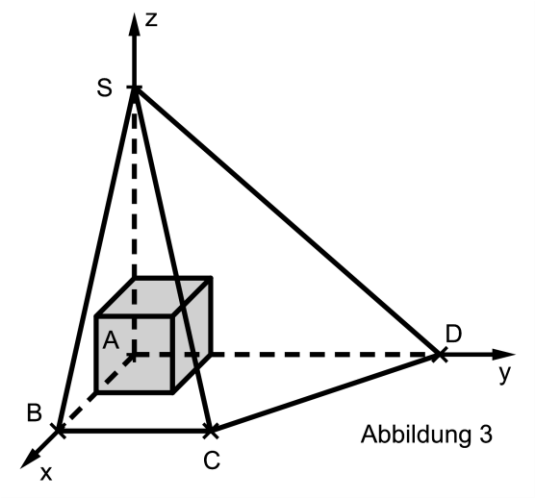
Betrachtet werden die Würfel, von denen drei Seitenflächen in den drei Koordinatenebenen liegen.
Abbildung 3 zeigt einen dieser Würfel.
Unter diesen Würfeln gibt es einen, bei dem ein Eckpunkt auf der Kante $\overline{CS}$ der Pyramide liegt.
Berechnen Sie die Kantenlänge dieses Würfels und begründen Sie, dass kein Punkt dieses Würfels außerhalb der Pyramide liegt. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Berechne die Kantenlänge dieses Würfels
Unter diesen Würfeln gibt es einen, bei dem ein Eckpunkt auf der Kante $\overline{CS}$ der Pyramide liegt.
Berechne die Geradengleichung $g_{CS}$ :
$g_{CS}:\;\vec x=\overrightarrow{OC}+r\cdot \left(\overrightarrow{OS}-\overrightarrow{OC}\right)=\begin{pmatrix}2\\2\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}$
Vom Punkt $A$ aus zeigt ein Vektor mit drei gleichen Komponenten zu einem Punkt auf der Geraden $g_{CS}$ :
$\begin{pmatrix}a\\a\\a\end{pmatrix}=\begin{pmatrix}2\\2\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\-2\\3{,}5\end{pmatrix}$
Aus Gleichung $\mathrm{(III)}$ folgt: $r=\dfrac{a}{3{,}5}$
$r=\dfrac{a}{3{,}5}$ eingesetzt in Gleichung $\mathrm{(I)}$ : $a=2-\dfrac{2a}{3{,}5}$
Die Kantenlänge $a$ des Würfels ist somit $\dfrac{14}{11}$ .
Begründe, dass kein Punkt dieses Würfels außerhalb der Pyramide liegt
In Verbindung mit der Abbildung genügt es zu prüfen, ob der Eckpunkt $\left(\frac{14}{11}|0| \frac{14}{11}\right)$ des Würfels außerhalb der Pyramide liegt.
Berechne die Geradengleichung $g_{BS}$ :
$g_{BS}:\;\vec x=\overrightarrow{OB}+r\cdot \left(\overrightarrow{OS}-\overrightarrow{OB}\right)=\begin{pmatrix}2\\0\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\0\\3{,}5\end{pmatrix}$
Prüfe, ob der obige Eckpunkt auf $g_{BS}$ liegt:
$\begin{pmatrix}\frac{14}{11}\\0\\\frac{14}{11}\end{pmatrix}=\begin{pmatrix}2\\0\\0\end{pmatrix}+r\cdot \begin{pmatrix}-2\\0\\3{,}5\end{pmatrix}$
Aus Gleichung $\mathrm{(III)}$ folgt: $r=\dfrac{14}{11\cdot 3{,}5}=\dfrac{4}{11}$
$r=\dfrac{4}{11}$ eingesetzt in Gleichung $\mathrm{(I)}$ :
$\dfrac{14}{11}=2-\dfrac{8}{11}=\dfrac{14}{11}\;\checkmark$
Da die Gleichung mit $r= \dfrac{4}{11}$ eine Lösung besitzt, liegt der Eckpunkt auf der Kante $\overline{BS}$ und nicht außerhalb der Pyramide.

Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne die Geradengleichung $g_{CS}$ .
Vom Punkt $A$ aus zeigt ein Vektor mit drei gleichen Komponenten zu einem Punkt auf der Geraden $g_{CS}$ .
Löse diese Gleichung.
Teil 2
In Verbindung mit der Abbildung genügt es zu prüfen, ob der Eckpunkt $\left(x|0| x\right)$ des Würfels außerhalb der Pyramide liegt.
Berechne die Geradengleichung $g_{BS}$ .
Prüfe, ob der Eckpunkt auf $g_{BS}$ liegt.

6

Aufgabe 3B

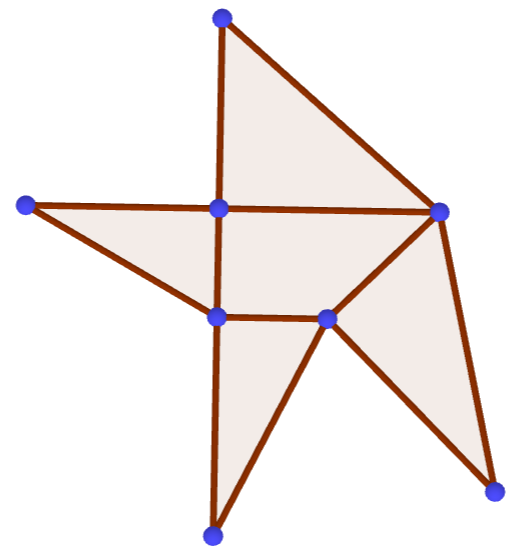
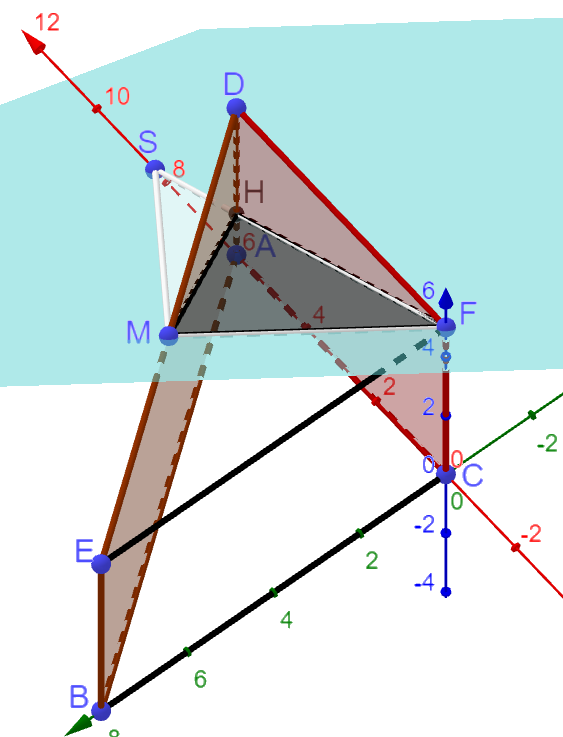
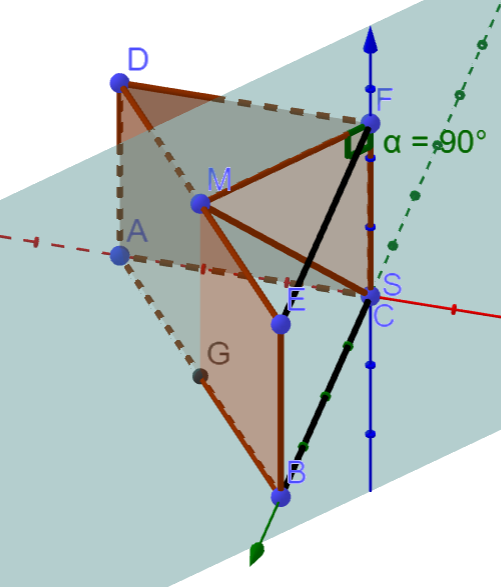
Gegeben sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 ∣ 0 ∣ 0), D (6 ∣ 0 ∣ 5)$ , $E (0 ∣ 8 ∣ 5)$ und $F (0 ∣ 0 ∣ 5)$ sowie der Punkt $M (3 ∣ 4 ∣ 5)$ (vgl. Abbildung 1).

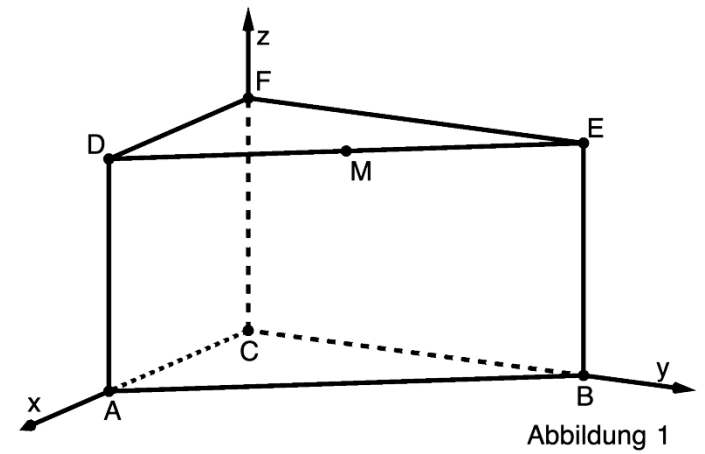
Berechnen Sie den Inhalt der Oberfläche des Prismas. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
Berechne den Inhalt der Oberfläche des Prismas
Für die Oberflächenberechnung werden verschiedene Vektoren und ihre Beträge benötigt.
$\overrightarrow{DE}=\overrightarrow{OE}-\overrightarrow{OD}=\begin{pmatrix}0\\8\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-6\\8\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DE}\Big\vert=\sqrt{(-6)^2+8^2+0}=\sqrt{100}=10$
$\overrightarrow{DF}=\overrightarrow{OF}-\overrightarrow{OD}=\begin{pmatrix}0\\0\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-6\\0\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DF}\Big\vert=6$
$\overrightarrow{FE}=\overrightarrow{OE}-\overrightarrow{OF}=\begin{pmatrix}0\\8\\5\end{pmatrix}-\begin{pmatrix}0\\0\\5\end{pmatrix}=\begin{pmatrix}0\\8\\0\end{pmatrix}\\\Big\vert\overrightarrow{FE}\Big\vert=8$
Die Höhe des Prismas ist $h = 5$ .
Dann folgt für den Oberflächeninhalt des Prismas:
$O_\text{Prisma}=\Big\vert\overrightarrow{DF}\Big\vert\cdot h+\Big\vert\overrightarrow{EF}\Big\vert\cdot h+\Big\vert\overrightarrow{DE}\Big\vert\cdot h+2\cdot \dfrac{1}{2}\cdot \Big\vert\overrightarrow{DF}\Big\vert\cdot \Big\vert\overrightarrow{EF}\Big\vert$
$O_\text{Prisma}=(6+8+10)\cdot 5+2\cdot \dfrac{1}{2}\cdot 6\cdot 8=168$
Der Inhalt der Oberfläche des Prismas beträgt $168\; \text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Vektoren $\overrightarrow{DE}$ , $\overrightarrow{DF}$ und $\overrightarrow{FE}$ und ihre Beträge.
Die Höhe des Prismas ist die z-Koordinate eines in der Deckfläche liegenden Punktes.
Begründen Sie, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$
liegen. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einführung zum Kreis
Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen
Berechne die Vektoren $\overrightarrow{DM}, \overrightarrow{FM}$ und $\overrightarrow{EM}$ , sowie ihre Beträge.
$\overrightarrow{DM}=\overrightarrow{OM}-\overrightarrow{OD}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}6\\0\\5\end{pmatrix}=\begin{pmatrix}-3\\4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{DM}\Big\vert=\sqrt{(-3)^2+4^2+0}=\sqrt{25}=5$
$\overrightarrow{FM}=\overrightarrow{OM}-\overrightarrow{OF}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}0\\0\\5\end{pmatrix}=\begin{pmatrix}3\\4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{FM}\Big\vert=\sqrt{3^2+4^2+0}=\sqrt{25}=5$
$\overrightarrow{EM}=\overrightarrow{OM}-\overrightarrow{OE}=\begin{pmatrix}3\\4\\5\end{pmatrix}-\begin{pmatrix}0\\8\\5\end{pmatrix}=\begin{pmatrix}3\\-4\\0\end{pmatrix}$
$\Big\vert\overrightarrow{EM}\Big\vert=\sqrt{3^2+(-4)^2+0}=\sqrt{25}=5$
Es gilt: $\Big\vert\overrightarrow{DM}\Big\vert= \Big\vert\overrightarrow{FM}\Big\vert= \Big\vert\overrightarrow{EM}\Big\vert=5$
Alle Punkte liegen zusammen mit $M$ in einer Ebene und haben den gleichen Abstand $5$ vom Punkt $M$ und liegen deshalb auf einem Kreis um $M$ mit dem Radius $5$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Vektoren $\overrightarrow{DM}, \overrightarrow{FM}$ und $\overrightarrow{EM}$ , sowie ihre Beträge.
Berechnen Sie den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
Berechne den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt
Berechne den Vektor $\overrightarrow{MA}$ :
$\overrightarrow{MA}=\overrightarrow{OA}-\overrightarrow{OM}=\begin{pmatrix}6\\0\\0\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}3\\-4\\-5\end{pmatrix}$
Der Vektor $\vec n=\begin{pmatrix}1\\0\\0\end{pmatrix}$ .
Für den Winkel zwischen den beiden Vektoren gilt:
$\cos\alpha=\dfrac{|\vec{n}\circ\overrightarrow{MA}|}{|\vec{n}|\cdot|\overrightarrow{MA}|}=\dfrac{\left|\begin{pmatrix}1\\0\\0\end{pmatrix}\circ\begin{pmatrix}3\\-4\\-5\end{pmatrix}\right|}{1\cdot \sqrt{3^2+(-4)^2+(-5)^2}}=\dfrac{3}{\sqrt{50}}$
$\alpha=\cos^{-1}\left(\dfrac{3}{\sqrt{50}}\right)\approx 64{,}9^\circ$
Der Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt, beträgt rund $65^\circ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne den Vektor $\overrightarrow{MA}$ .
Die x-Achse wird durch den Vektor $\begin{pmatrix}1\\0\\0\end{pmatrix}$ dargestellt.
Für den Winkel zwischen zwei Vektoren gilt: $\cos\alpha=\dfrac{|\vec{a}\circ\vec{b}|}{|\vec{a}|\cdot|\vec{b}|}$
Durch
$\def\arraystretch{1.25} \vec x= \left(\begin{array}{} 0\\0 \\5 \end{array}\right) + \lambda \left(\begin{array}{}3 \\4 \\0 \end{array}\right) + \mu \left(\begin{array}{} 7{,}5\\ 0\\-5 \end{array}\right)$
mit $\lambda, \mu \in\mathbb{R}$ ist die Ebene $H$ gegeben.
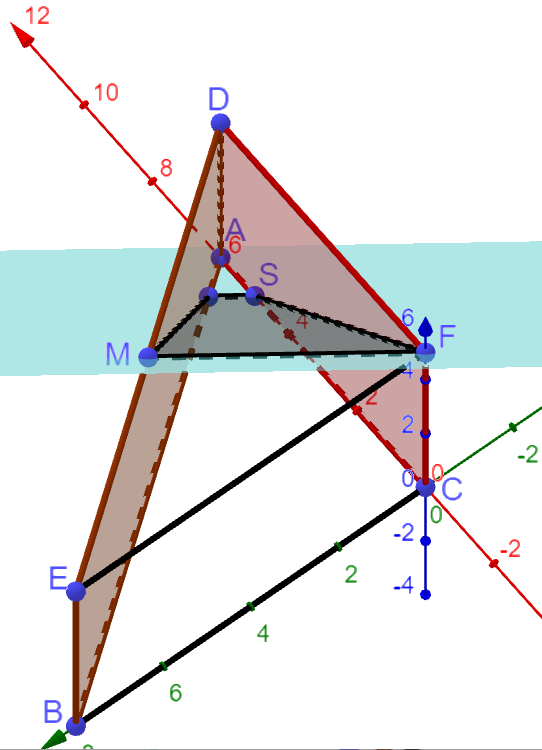
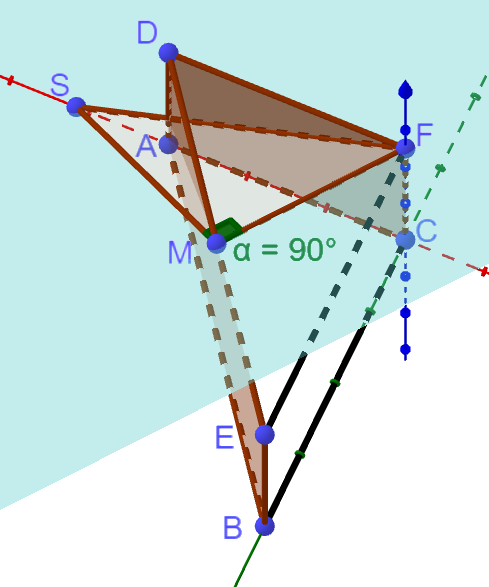
Die Punkte $M, F$ und $S (7,5 ∣ 0 ∣ 0)$ liegen in der Ebene $H$ (vgl. Abbildung 2).
Im Folgenden sind zwei Schritte zum Lösen einer Aufgabe angegeben, die im Zusammenhang mit den betrachteten geometrischen Objekten steht:
$\def\arraystretch{1.25} \left(\begin{array}{} 6\\0 \\1\end{array}\right) = \left(\begin{array}{} 0\\0 \\5 \end{array}\right) + \lambda \left(\begin{array}{} 3\\4 \\0 \end{array}\right) + \mu \left(\begin{array}{} 7{,}5\\0 \\-5 \end{array}\right)$
$\def\arraystretch{1.25} \left(\begin{array}{} 6\\0 \\1 \end{array}\right) = \left(\begin{array}{} 6\\0 \\0 \end{array}\right) + r\left(\begin{array}{} 0\\0 \\5 \end{array}\right)$ mit $r \in\mathbb{R}$
Geben Sie eine passende Aufgabenstellung an. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung von Punkten, Geraden und Ebenen
Gib eine passende Aufgabenstellung an
In Gleichung $\mathrm{(I)}$ wird eine Punktprobe durchgeführt. Es wird geprüft, ob der Punkt $(6 ∣ 0 ∣ 1)$ in der Ebene $H$ liegt.
In Gleichung $\mathrm{(II)}$ wird ebenfalls eine Punktprobe durchgeführt. Es wird geprüft, ob der Punkt $(6 ∣ 0 ∣ 1)$ auf der Geraden durch die Punkte $A$ und $D$ liegt.
Aufgabenstellung: Untersuche, ob der Punkt $(6 ∣ 0 ∣ 1)$ sowohl in der Ebene $H$ als auch auf der Geraden durch $A$ und $D$ liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es werden zwei Punktproben für den Punkt $(6 ∣ 0 ∣ 1)$ durchgeführt.
Wo soll der Punkt liegen?
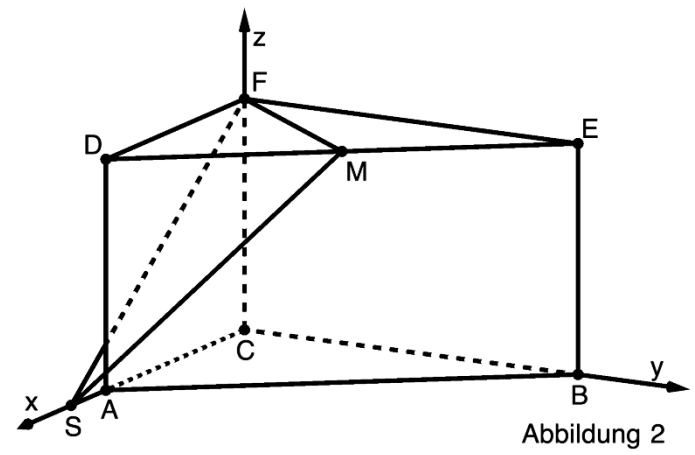
Anstelle des Punkts $S$ werden nun Punkte $S_{t} (t ∣ 0 ∣ 0)$ mit $t\geq 0$ auf der x-Achse betrachtet.
Für jeden Wert von $t$ schneidet die Ebene durch die Punkte $M, F$ und $S_{t}$ das Prisma
$A B C D E F$ in einem Vieleck.
Geben Sie die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an. [4 BE]

Gib die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an
Maßgebend für die Art des Vielecks ist die x-Koordinate von $A$ : $x = 6$
Für $t\geq 6$ besitzt das Vieleck drei Ecken.
Für $0 \leq t < 6$ besitzt das Vieleck vier Ecken.
Zur Veranschaulichung: Vieleck mit drei Ecken
Hier hat $t$ den Wert $\dfrac{25}{3}>6$ .
Das weiß umrandete Dreieck liegt in der Ebene durch die Punkte $M, F$ und $S_{t}$ .
Das schwarze Dreieck ist die Schnittfläche der Ebene mit dem Prisma.
Zur Veranschaulichung: Vieleck mit vier Ecken
Hier hat $t$ den Wert $5 < 6$ .
Das schwarze Viereck ist die Schnittfläche der Ebene mit dem Prisma.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Maßgebend für die Art des Vielecks ist die x-Koordinate von $A$ : $x = 6$
Bestimmen Sie die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Bestimme die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist
Möglichkeit 1
Für $t = 0$ liegt der Punkt $S$ auf dem Punkt $C$ . Dann befindet sich ein rechter Winkel im Punkt $F$ .
Skizze zur Veranschaulichung:
Möglichkeit 2
Berechne das Skalarprodukt der beiden Vektoren $\overrightarrow{MF}$ und $\overrightarrow{MS_t}$ . Es muss für einen rechten Winkel bei $M$ gleich null sein.
$\overrightarrow{MF}=\overrightarrow{OF}-\overrightarrow{OM}=\begin{pmatrix}0\\0\\5\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}-3\\-4\\0\end{pmatrix}$
$\overrightarrow{MS_t}=\overrightarrow{OS_t}-\overrightarrow{OM}=\begin{pmatrix}t\\0\\0\end{pmatrix}-\begin{pmatrix}3\\4\\5\end{pmatrix}=\begin{pmatrix}t-3\\-4\\-5\end{pmatrix}$
$\overrightarrow{MF}\circ \overrightarrow{MS_t}=\begin{pmatrix}-3\\-4\\0\end{pmatrix}\circ \begin{pmatrix}t-3\\-4\\-5\end{pmatrix}=-3\cdot(t-3)+(-4)\cdot(-4)=0$
$\Rightarrow\; -3t+9+16=0\;\Rightarrow\;t=\dfrac{25}{3}$
Für $t=\dfrac{25}{3}$ liegt der rechte Winkel im Punkt $M$ .
Skizze zur Veranschaulichung:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Möglichkeit 1:
Überlege Dir, wo der Punkt $S$ für $t = 0$ liegt.
Möglichkeit 2:
Berechne das Skalarprodukt der beiden Vektoren $\overrightarrow{MF}$ und $\overrightarrow{MS_t}$ .

Wahlteil - CAS

Aufgabe 1A

Zeige rechnerisch, dass der Graph von fff keine weiteren Extrempunkte besitzt

Hast du eine Frage oder Feedback?

Ermittle eine Gleichung von ttt

Weise rechnerisch nach, dass ttt die Tangente an den Graphen von fff im Punkt (5∣f(5))(5|f(5))(5∣f(5)) ist

Hast du eine Frage oder Feedback?

Berechne den Inhalt dieser Fläche

Hast du eine Frage oder Feedback?

Gib in diesem Zusammenhang die Bedeutung von aaa und bbb an

Berechne die Werte von 𝑎𝑎a und 𝑏𝑏b

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gib diese konstante Geschwindigkeit an

Zeige durch Rechnung, dass der zum Radfahrer HHH gehörende Graph in der Abbildung 2 an der Stelle 121212 eine waagerechte Tangente aufweist

Hast du eine Frage oder Feedback?

Berechne xsx_sxs​

Hast du eine Frage oder Feedback?

Berechne, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt

Hast du eine Frage oder Feedback?

Aufgabe 1B

Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.

Bestimme den Zeitpunkt, zu dem die Wassertemperatur 12∘C12^\circ C12∘C beträgt

Hast du eine Frage oder Feedback?

Berechne die Werte der folgenden Terme und interpretiere diese im Sachzusammenhang

Hast du eine Frage oder Feedback?

Begründe anhand des Funktionsterms, dass der Funktionswert h(x)h(x)h(x) nur für −1<x<1−1 < x < 1−1<x<1 positiv ist

Hast du eine Frage oder Feedback?

Gib die notwendigen Schritte zur Berechnung einer Gleichung von vvv an und erläutere diese

Hast du eine Frage oder Feedback?

Berechne die Wendestellen von hhh

Berechne den Wert der maximalen Steigung

Hast du eine Frage oder Feedback?

Für einen Wert von www ist der Flächeninhalt des Dreiecks maximal

Berechne den maximalen Flächeninhalt

Hast du eine Frage oder Feedback?

Gib eine Gleichung an, mit der die x-Koordinate von PPP bestimmt werden kann

Veranschauliche den Aufbau der Gleichung in Abbildung 2

Hast du eine Frage oder Feedback?

Aufgabe 2A

Interpretiere die Gleichung P(T‾∩M)=0,05P(\overline{T} \cap M)=0{,}05P(T∩M)=0,05 im Sachzusammenhang

Hast du eine Frage oder Feedback?

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit dafür, dass die ausgewählte Person entweder ein Treuekunde oder ein Morgenkunde ist

Hast du eine Frage oder Feedback?

Untersuche, ob die Ereignisse TTT und MMM stochastisch unabhängig sind

Hast du eine Frage oder Feedback?

Stelle das dem Gewinnspiel zugrundeliegende Zufallsexperiment in einem beschrifteten Baumdiagramm dar

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit dafür, dass dabei genau viermal der kleinstmögliche Rabatt erzielt wird und dies bei vier Personen unmittelbar hintereinander

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit qqq, wenn beim Glücksspiel mit dem Glücksrad auf lange Sicht im Mittel ein Rabatt von 9 %9 \;\%9% erzielt werden soll

Hast du eine Frage oder Feedback?

Aufgabe 2B

Zeige, dass P(L‾∩D‾)=0,28P(\overline{L} \cap \overline{D})=0{,}28P(L∩D)=0,28 gilt

Gib das zugrundeliegende Ereignis im Sachzusammenhang an

Hast du eine Frage oder Feedback?

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar

Gib die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar einen Laptop, jedoch keinen Desktop-PC besitzt

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit dafür, dass höchstens 70 %70\; \%70% dieser 900900900 Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen

Hast du eine Frage oder Feedback?

Berechne den Erwartungswert μ\muμ von XXX

Ermittele die kleinste mögliche natürliche Zahl kkk, sodass P(μ−k≤X≤μ)≥30 %P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%P(μ−k≤X≤μ)≥30% gilt

Hast du eine Frage oder Feedback?

Ergänze im dargestellten Koordinatensystem die Skalierungen der Achsen und erläutere Dein Vorgehen

Hast du eine Frage oder Feedback?

Aufgabe 3A

Begründe, dass die Grundfläche der Pyramide ein Trapez ist

Berechne das Volumen der Pyramide

Hast du eine Frage oder Feedback?

Zeige, dass das Dreieck CDSCDSCDS im Punkt CCC rechtwinklig ist

Hast du eine Frage oder Feedback?

Ergänze Abbildung 2 so, dass ein vollständiges Netz der Pyramide ABCDSABCDSABCDS dargestellt ist

Hast du eine Frage oder Feedback?

Untersuche, ob der Punkt P(4∣−8∣7)P(4|−8|7)P(4∣−8∣7) in der Ebene liegt, in der die Seitenfläche CDSCDSCDS liegt

Hast du eine Frage oder Feedback?

Zeige rechnerisch, dass der Graph von $f$ keine weiteren Extrempunkte besitzt

Ermittle eine Gleichung von $t$

Weise rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ ist

Gib in diesem Zusammenhang die Bedeutung von $a$ und $b$ an

Berechne die Werte von $𝑎$ und $𝑏$

Zeige durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist

Berechne $x_{s}$

Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt

Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist

Gib die notwendigen Schritte zur Berechnung einer Gleichung von $v$ an und erläutere diese

Berechne die Wendestellen von $h$

Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal

Gib eine Gleichung an, mit der die x-Koordinate von $P$ bestimmt werden kann

Interpretiere die Gleichung $P(\overline{T} \cap M)=0{,}05$ im Sachzusammenhang

Untersuche, ob die Ereignisse $T$ und $M$ stochastisch unabhängig sind

Berechne die Wahrscheinlichkeit $q$ , wenn beim Glücksspiel mit dem Glücksrad auf lange Sicht im Mittel ein Rabatt von $9 %$ erzielt werden soll

Zeige, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt

Berechne die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen

Berechne den Erwartungswert $μ \mu$ von $X$

Ermittele die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt

Zeige, dass das Dreieck $C D S$ im Punkt $C$ rechtwinklig ist

Ergänze Abbildung 2 so, dass ein vollständiges Netz der Pyramide $A B C D S$ dargestellt ist

Untersuche, ob der Punkt $P (4 ∣ - 8 ∣ 7)$ in der Ebene liegt, in der die Seitenfläche $C D S$ liegt

Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen

Berechne den Winkel, den die Strecke $\overline{AM}$ mit der x-Achse einschließt

Gib die Anzahl der Ecken des Vielecks in Abhängigkeit von $t$ an

Bestimme die beiden Werte von $t$ , für die das Dreieck $M F S_{t}$ rechtwinklig ist