Wahlteil - CAS - lernen mit Serlo!

Aufgabe 2B

Eine umfassende Studie zu den Arbeits- und Lebensbedingungen von Studierenden einer

Universität ergab, dass $56 %$ der Studierenden einen Laptop und $33 %$ einen Desktop-PC

besitzen. $72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte.

Unter den Studierenden der Universität wird eine Person zufällig ausgewählt und zum Besitz von digitalen Endgeräten befragt. Folgende Ereignisse werden betrachtet:

$L$ : „Die Person besitzt einen Laptop.“
$D$ : „Die Person besitzt einen Desktop-PC.“

Zeigen Sie, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt, und geben Sie das zugrundeliegende Ereignis im Sachzusammenhang an. [3 BE]
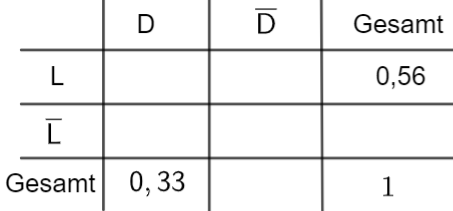
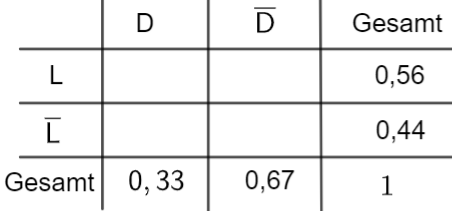
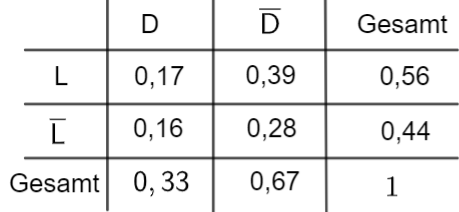
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Zeige, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt
$72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte.
$\Rightarrow\; P(L\cap D)+P(L\cap \overline{D})+P( \overline{L}\cap D)=0{,}72$
$\Rightarrow\;P(\overline{L} \cap \overline{D})=1-\left(P(L\cap D)+P(L\cap \overline{D})+P( \overline{L}\cap D)\right)=1-0{,}72=0{,}28$
Gib das zugrundeliegende Ereignis im Sachzusammenhang an
Ereignis: Die ausgewählte Person besitzt weder einen Laptop noch einen
Desktop-PC.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
$72 %$ der Studierenden haben mindestens eines dieser beiden Endgeräte. Gib dazu das Gegenereignis an.
Teil 2
Was bedeuten $\overline{L}$ und $\overline{D}$ . Wie lautet das zugehörige Ereignis?
Stellen Sie den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.
Geben Sie die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar
einen Laptop, jedoch keinen Desktop-PC besitzt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar
Laut Aufgabenstellung haben $56 %$ der Studierenden einen Laptop und $33 %$ besitzen einen Desktop-PC.
Mit diesen beiden Angaben beginnt die Vierfeldertafel:
Zunächst können durch Differenzbildung zwei weitere Felder ausgefüllt werden:
Aus Aufgabe a) folgt: $P(\overline{L} \cap \overline{D})=0{,}28$ . Dieser Wert wird eingetragen.
Dann ist $P({L} \cap \overline{D})=0{,}67-0{,}28=0{,}39$ und $P(\overline{L} \cap {D})=0{,}44-0{,}28=0{,}16$ .
Der letzte Wert ist dann $P({L} \cap {D})=0{,}33-0{,}16=0{,}17$ .
Die vollständige Vierfeldertafel sieht dann so aus:
Gib die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar einen Laptop, jedoch keinen Desktop-PC besitzt
Gesucht ist hier die Wahrscheinlichkeit $P(L\cap \overline{D})$ .
Aus der Vierfeldertafel entnimmt man: $P(L \cap \overline{D})=0{,}39$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Laut Aufgabenstellung haben $56 %$ der Studierenden einen Laptop und $33 %$ besitzen einen Desktop-PC. Trage diese Werte ein und ergänze die Differenzwerte zu $1$ .
Aus Aufgabe a) kann ein weiterer Wert in die Tafel eingetragen werden. Die restlichen Werte erfolgen durch Differenzbildung.
Teil 2
Gesucht ist hier die Wahrscheinlichkeit $P(L\cap \overline{D})$ .
Nun wird unter allen Befragten, die einen Desktop-PC haben, eine Person zufällig
ausgewählt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Berechne die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt
Gesucht ist $P_{D} (L)$ :
Mit den Werten aus der Vierfeldertafel folgt:
$P_D(L)=\dfrac{P(L\cap D)}{P(D)}=\dfrac{0{,}17}{0{,}33}\approx0{,}52$
Die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt, beträgt rund $52 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne mit den Werten aus der Vierfeldertafel $P_D(L)=\dfrac{P(L\cap D}{P(D)}$ .
In derselben Studie wurde auch festgestellt, dass $68 %$ der Besitzer von Laptops und
Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen.
Unter den Besitzern dieser Endgeräte werden $900$ Personen zufällig ausgewählt. Die
Zufallsgröße $X$ beschreibt die Anzahl derjenigen unter diesen $900$ Personen, die versuchen, ein Software-Problem selbstständig zu lösen. Dabei wird $X$ als binomialverteilt angenommen.
Berechnen Sie die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen
bei einem Software-Problem versuchen, dieses selbstständig zu lösen. [2 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Berechne die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen
$70 %$ dieser $n = 900$ Personen sind $630$ Personen.
Gegeben ist weiterhin, dass $68 %$ der Besitzer von Laptops und
Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen $\;\Rightarrow\;p=0{,}68$
Gesucht ist die Wahrscheinlichkeit: $P(X\leq 630)=\text{binomCdf}(900;0{,}68;0;630)\approx0{,}9075$
Die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen, beträgt rund $91 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $70 %$ von $n = 900$ Personen.
Gegeben ist, dass $68 %$ der Besitzer von Laptops und Desktop-PCs bei einem Software-Problem versuchen, dieses selbstständig zu lösen.
Berechne $P(X\leq 70\;\%\text{ von}\; 900)$ .
Berechnen Sie den Erwartungswert $μ \mu$ von $X$ und ermitteln Sie die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Berechne den Erwartungswert $μ \mu$ von $X$
Es ist $\mu=n\cdot p=900\cdot 0{,}68=612$
Der Erwartungswert von $X$ beträgt $612$ .
Ermittele die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt
Gefordert ist: $P(\mu − k ≤ X ≤ \mu) ≥ 0{,}3$
$\Rightarrow\;P(612− k ≤ X ≤ 612) ≥ 0{,}3$
Man findet:
$P(600 ≤ X ≤ 612) \approx 0{,}3269 > 0{,}3$
$P(601 ≤ X ≤ 612) \approx 0{,}3072>0{,}3$
$P(602 ≤ X ≤ 612) \approx 0{,}2866<0{,}3$
Also ist hier die richtige Lösung: $P(612− 11 ≤ X ≤ 612)\approx0{,}3072>0{,}3\;\Rightarrow\;k=11$
Die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt, ist $k = 11$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Es ist $\mu=n\cdot p$ .
Teil 2
Gefordert ist: $P(\mu − k ≤ X ≤ \mu) ≥ 0{,}3$
Setze $μ \mu$ in die Ungleichung ein und probiere einige Werte für $k$ aus, sodass die Ungleichung gerade erfüllt wird.
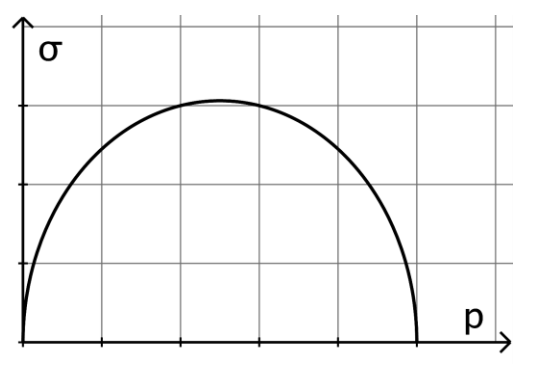
Für binomialverteilte Zufallsgrößen mit den Parametern $n = 15000$ und $p$ ist in der Abbildung die Standardabweichung $\sigma$ in Abhängigkeit von $p$ dargestellt.
Ergänzen Sie im dargestellten Koordinatensystem die
Skalierungen der Achsen und
erläutern Sie Ihr Vorgehen. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Ergänze im dargestellten Koordinatensystem die Skalierungen der Achsen und erläutere Dein Vorgehen
Es gilt: $0\leq p\leq 1$
Deshalb muss die rechte Grenze des Graphens auf der p-Achse $1$ sein.
(Ein Kästchen auf der p-Achse entspricht dann $0,2$ .)
Bei $p = 0,4$ (in der Skizze eingetragen) kann der $\sigma$ -Wert genau bestimmt werden.
Es ist $\sigma=\sqrt{n\cdot p\cdot(1-p)}$ .
Mit $n = 15000$ und $p = 0,4$ folgt dann:
$\sigma=\sqrt{15000\cdot 0{,}4\cdot 0{,}6}=60$
(Ein Kästchen auf der $\sigma$ -Achse entspricht dann $20$ .)
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es gilt: $0\leq p\leq 1$
Die rechte Grenze des Graphens ist damit bestimmt.
Bei einem bestimmten p-Wert kann der $\sigma$ -Wert genau bestimmt werden.
Berechne $\sigma=\sqrt{n\cdot p\cdot(1-p)}$ .

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

Aufgabe 2B

Zeige, dass P(L‾∩D‾)=0,28P(\overline{L} \cap \overline{D})=0{,}28P(L∩D)=0,28 gilt

Gib das zugrundeliegende Ereignis im Sachzusammenhang an

Hast du eine Frage oder Feedback?

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar

Gib die Wahrscheinlichkeit dafür an, dass die zufällig ausgewählte Person zwar einen Laptop, jedoch keinen Desktop-PC besitzt

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit dafür, dass diese einen Laptop besitzt

Hast du eine Frage oder Feedback?

Berechne die Wahrscheinlichkeit dafür, dass höchstens 70 %70\; \%70% dieser 900900900 Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen

Hast du eine Frage oder Feedback?

Berechne den Erwartungswert μ\muμ von XXX

Ermittele die kleinste mögliche natürliche Zahl kkk, sodass P(μ−k≤X≤μ)≥30 %P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%P(μ−k≤X≤μ)≥30% gilt

Hast du eine Frage oder Feedback?

Ergänze im dargestellten Koordinatensystem die Skalierungen der Achsen und erläutere Dein Vorgehen

Hast du eine Frage oder Feedback?

Zeige, dass $P(\overline{L} \cap \overline{D})=0{,}28$ gilt

Berechne die Wahrscheinlichkeit dafür, dass höchstens $70 %$ dieser $900$ Personen bei einem Software-Problem versuchen, dieses selbstständig zu lösen

Berechne den Erwartungswert $μ \mu$ von $X$

Ermittele die kleinste mögliche natürliche Zahl $k$ , sodass $P(\mu − k ≤ X ≤ \mu) ≥ 30\;\%$ gilt