Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

Aufgabe 3: Kasimir Bastelt

Kasimir zeichnet ein gleichseitiges Dreieck mit der Seitenlänge a = 10 cm und einer Höhe

h ≈ 8,7 cm (Abbildung 1).

Bild

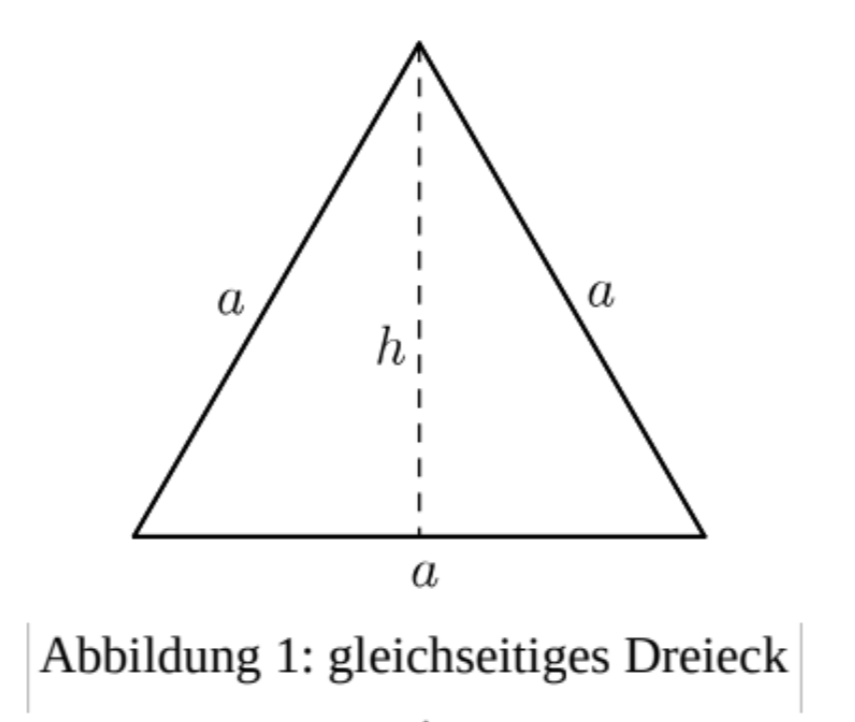
  1. Bestätige durch eine Rechnung, dass der Flächeninhalt des Dreiecks 43,5 cm2cm^2 beträgt.

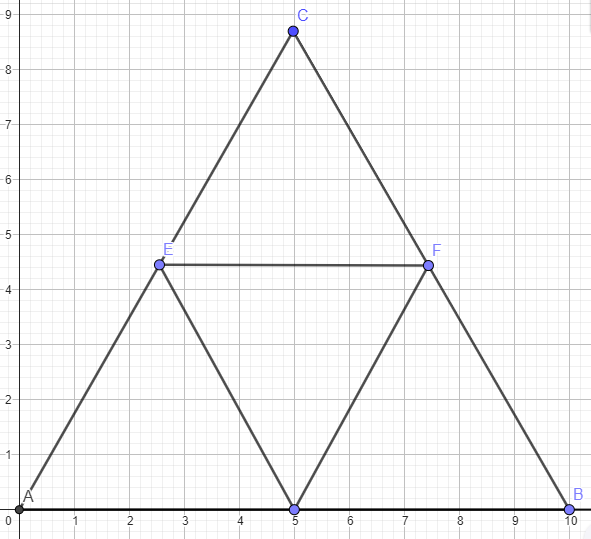
  2. Kasimir markiert auf jeder Dreieckseite den Mittelpunkt.

    Die Mittelpunkte verbindet er. Es entstehen vier gleiche kleine Dreiecke

    (Abbildung 2).

    Bild

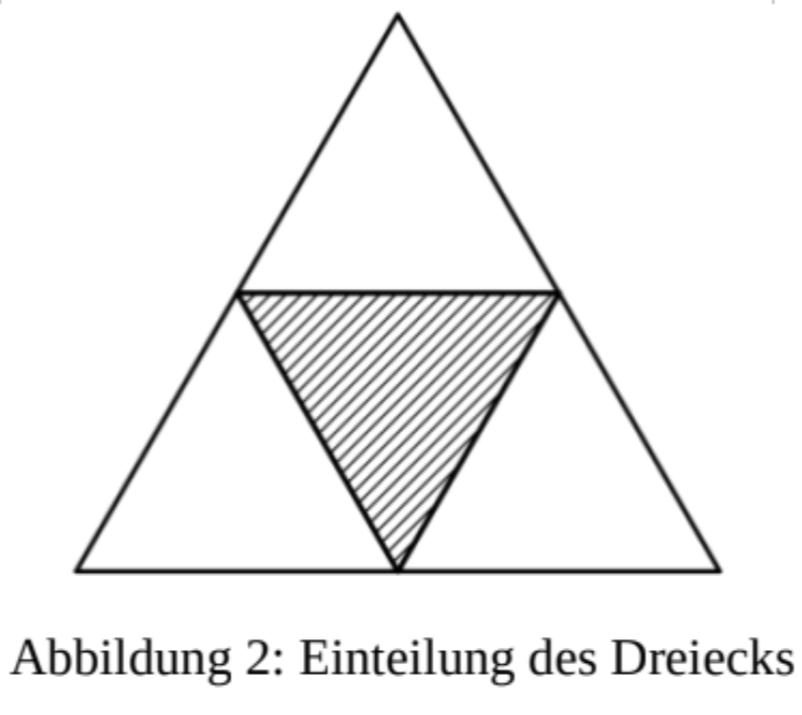
    Zeichne die Figur (Abbildung 2) mit den Originalmaßen auf ein DIN-A4-Blatt.

  3. Bestätige durch eine Rechnung, dass der Flächeninhalt eines kleinen Dreiecks

    ca. 10,9cm210{,}9 cm^2 beträgt.

  4. Kasimir klappt die drei äußeren hellen Dreiecke nach oben.

    Es entsteht eine besondere Pyramide, die Tetraeder genannt wird (Abbildung 3).

    Die Kantenlänge des Tetraeders

    beträgt 5 cm. Der Flächeninhalt der Grundfläche beträgt ca. 10,9cm210{,}9 cm^2.

    Bild

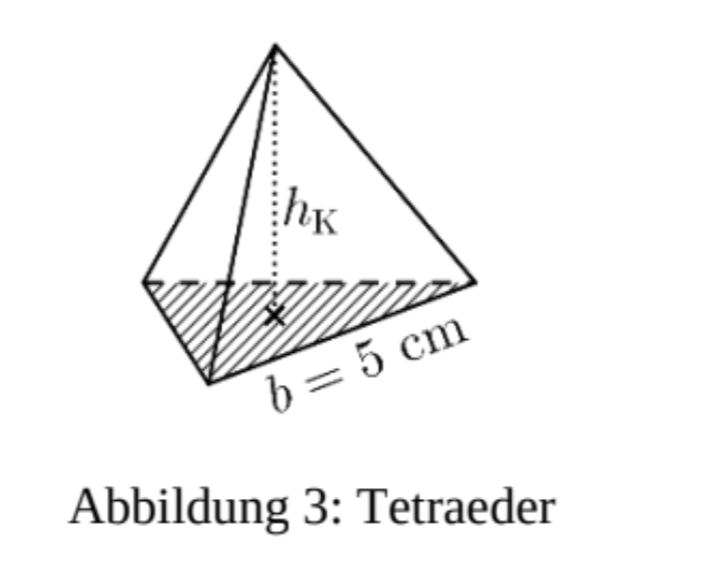
    Die Körperhöhe hKh_K eines Tetraeders kann mit folgender Formel berechnet werden:

    hK=63⋅bh_K = \frac {\sqrt 6}3 · b

    Zeige mit der Formel, dass hK≈4,1h_K ≈ 4{,}1 cm lang ist.

  5. Berechne mit der Körperhöhe hKh_K das Volumen des Tetraeders.

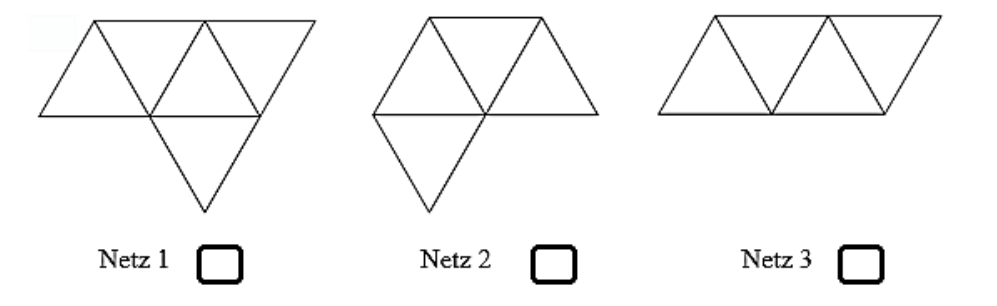
  6. Abbildung 2 stellt das Netz eines Tetraeders dar.

    Welches Netz stellt ebenfalls das Netz eines Tetraeders dar? Kreuze an.

    Bild