Teil 2, Analysis II - lernen mit Serlo!

Der Bestand einer Bakterienkultur, der kontinuierlich Gift zugeführt wird, kann in den ersten fünf Stunden näherungsweise durch eine Funktion des folgenden Typs beschrieben werden:

$k:t\mapsto 50t\cdot e^{-at}+10$ mit $t\in[0;5]$

Dabei gibt $t$ die seit Beginn der Giftzugabe zum Zeitpunkt $t_{0} = 0$ vergangene Zeit in Stunden an. Der Funktionswert $k (t)$ gibt die Anzahl der Bakterien in Tausend an. Je nach Wirksamkeit des Gifts ist $a$ eine dem Gift entsprechende positive reelle Zahl. Auf das Mitführen von Einheiten während der Rechnungen wird verzichtet. Runden Sie Ihre Ergebnisse sinnvoll. Die Abbildung zeigt drei Ausschnitte von Graphen der Funktion $k$ für drei verschiedene Werte für $a$ .

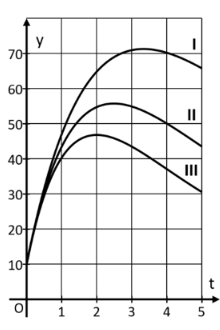
Graph I gilt für $a_1=0{,}3$ mit $k_I(t)=50t\cdot e^{-0{,}3t}+10$

Graph II gilt für $0{,}3\lt a_2\lt0{,}5$ mit $k_{II}(t)=50t\cdot e^{-a_2t}+10$

Graph III gilt für $a_3=0{,}5$ mit $k_{III}(t)=50t\cdot e^{-0{,}5t}+10$

Berechnen Sie für $t_{1} = 0$ und $t_{2} = 2$ den Quotienten $\dfrac{k_{III}(t_2)-k_{III}(t_1)}{t_2-t_1}$ und interpretieren Sie das Ergebnis im Sachzusammenhang.
Überprüfen Sie bei der Funktion $k_{III}$ rechnerisch, ob vier Stunden nach Beginn der Giftzugabe die momentane Abnahmerate der Anzahl der Bakterien ca. $113$ Bakterien pro Minute beträgt.
Entnehmen Sie der Abbildung ein geeignetes Wertepaar von Graph II und berechnen Sie damit den Wert $a_{2}$ für den Funktionsterm $k_{II}(t)$ . Folgern Sie aus den Angaben und dem berechneten Wert für $a_{2}$ , wie die Größe von $a$ mit der Wirksamkeit des Gifts zusammenhängt.