A I - lernen mit Serlo!

Einer Halbkugel mit Radius $R=10 \cm$ soll ein Zylinder mit Radius $r$ und Höhe $h$ einbeschrieben werden (siehe Skizze).

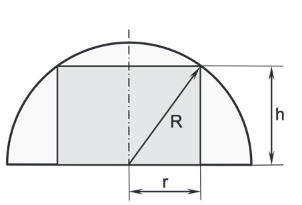
Bei Berechnungen kann auf die Verwendung von Einheiten verzichtet werden.

Ermitteln Sie die Maßzahl $V (h)$ des Volumens des Zylinders in Abhängigkeit von der Höhe $h$ und geben Sie eine sinnvolle Definitionsmenge für die Funktion $V:h\mapsto V(h)$ an, wenn die Höhe $h$ mindestens $6 \cm$ betragen soll.
[Mögliches Teilergebnis: $V(h)=h\pi(100-h^2)$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Ermittele die Maßzahl $V (h)$ des Volumens des Zylinders in Abhängigkeit von der Höhe $h$
Gegeben ist der Halbkugelradius $R=10 \cm$ .
$V_Z=\pi\cdot r^2\cdot h$
Wende im rechtwinkligen Dreieck den Satz des Pythagoras an:
$R^2=r^2+h^2\;\Rightarrow\;10^2=r^2+h^2\;\Rightarrow\;r^2=100-h^2$ .
Setze $r^{2}$ in $V_{Z}$ ein:
$V_Z(h)=\pi\cdot(100-h^2)\cdot h=\pi\cdot(100h-h^3)$
Die Maßzahl $V (h)$ des Volumens des Zylinders in Abhängigkeit von der Höhe $h$ lautet $V_Z(h)=\pi\cdot(100h-h^3)$ .
Gib eine sinnvolle Definitionsmenge für die Funktion $V:h\mapsto V(h)$ an, wenn die Höhe $h$ mindestens $6 \cm$ betragen soll
Es gilt also $h\geq 6$ und $h < 10$ (für $h = 10$ ist das Zylindervolumen gleich null).
Damit ist die Definitionsmenge $D_{V} = [6; 10 [$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Es ist $V_Z=\pi\cdot r^2\cdot h$ .
Wende im rechtwinkligen Dreieck den Satz des Pythagoras an und löse nach $r^{2}$ auf. Setze $r^{2}$ in $V_{Z}$ ein.
Teil 2
Es muss gelten $h\geq 6$ und $h < 10$ $\;\Rightarrow\;D_V$ .
Berechnen Sie $h$ so, dass $V (h)$ den absolut größten Wert annimmt, und untersuchen Sie, ob das maximale Volumen $V_{\text{max}}$ des Zylinders mehr als die Hälfte des Halbkugelvolumens beträgt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Berechne $h$ so, dass $V (h)$ den absolut größten Wert annimmt
Berechne die 1. und 2. Ableitung von $V_{Z} (h)$ .
Es ist $V_Z(h)=\pi\cdot(100h-h^3)\;\Rightarrow\;V'_Z(h)=\pi\cdot(100-3h^2)$ und
$V_Z''(h)=-6\cdot \pi\cdot h$
Die notwendige Bedingung für ein Extremum ist $V_{Z}^{'} (h) = 0$ .
Löse die Gleichung $V'_Z(h)=0\;\Rightarrow\;0=\pi\cdot(100-3h^2)$ nach $h$ auf.
$\Rightarrow\;h^2=\dfrac{100}{3}\;\Rightarrow\;h=\pm \sqrt{\dfrac{100}{3}}$
Die negative Lösung für $h$ entfällt und die positive Lösung $h= \sqrt{\dfrac{100}{3}}\approx5{,}77$ ist nicht im Definitionsbereich (siehe Aufgabe a) enthalten.
Das maximale Volumen kann also nur am Rand liegen $\;\Rightarrow\;$ Randbetrachtung.
Die linke Seite des Definitionsbereiches ist $h=6\;\Rightarrow\; V_Z(6)=\pi\cdot(100\cdot 6-6^3)=\pi\cdot 384$ .
Für die rechte Seite des Definitionsbereiches muss der Grenzwert berechnet werden: $\displaystyle\lim_{h\rightarrow 10^-}\pi\cdot(100h-h^3)=0$
Damit erhält man das absolute Maximum für $h=6\;\Rightarrow\;V_{max}=384 \pi$ .
Untersuche, ob das maximale Volumen $V_{\text{max}}$ des Zylinders mehr als die Hälfte des Halbkugelvolumens beträgt
Die Hälfte des Halbkugelvolumens ist $\dfrac{1}{4}$ des Kugelvolumens:
$\dfrac{1}{4}V_K=\dfrac{1}{4}\left(\dfrac{4}{3}\pi R^3\right)=\left(\dfrac{1}{3}\pi R^3\right)=\left(\dfrac{1}{3}\pi 10^3\right)=\dfrac{1000}{3}\pi\approx333{,}3\pi$
Gilt: $V_{max}>\dfrac{1}{4}V_K$ ?
$\Rightarrow\;384\pi>333{,}3\pi\;\checkmark$
Das maximale Volumen $V_{\text{max}}$ des Zylinders beträgt mehr als die Hälfte des Halbkugelvolumens.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne die 1. und 2. Ableitung von $V_{Z} (h)$ .
Die notwendige Bedingung für ein Extremum ist $V_{Z}^{'} (h) = 0$ .
Löse die Gleichung $V_{Z}^{'} (h) = 0$ nach $h$ auf.
Untersuche, ob die gefundene Lösung im Definitionsbereich liegt. Falls die nicht der Fall sein sollte, muss eine Randbetrachtung erfolgen.
Gib $V_{max}$ an.
Teil 2
Die Hälfte des Halbkugelvolumens ist $\dfrac{1}{4}$ des Kugelvolumens. Berechne diesen Wert.
Gilt: $V_{max}>\dfrac{1}{4}V_K$ ?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Ermittele die Maßzahl V(h)V(h)V(h) des Volumens des Zylinders in Abhängigkeit von der Höhe hhh

Gib eine sinnvolle Definitionsmenge für die Funktion V:h↦V(h)V:h\mapsto V(h)V:h↦V(h) an, wenn die Höhe hhh mindestens 6 cm6 \cm6 cm betragen soll

Hast du eine Frage oder Feedback?

Berechne hhh so, dass V(h)V(h)V(h) den absolut größten Wert annimmt

Untersuche, ob das maximale Volumen VmaxV_{\text{max}}Vmax​ des Zylinders mehr als die Hälfte des Halbkugelvolumens beträgt

Hast du eine Frage oder Feedback?

Ermittele die Maßzahl $V (h)$ des Volumens des Zylinders in Abhängigkeit von der Höhe $h$

Gib eine sinnvolle Definitionsmenge für die Funktion $V:h\mapsto V(h)$ an, wenn die Höhe $h$ mindestens $6 \cm$ betragen soll

Berechne $h$ so, dass $V (h)$ den absolut größten Wert annimmt

Untersuche, ob das maximale Volumen $V_{\text{max}}$ des Zylinders mehr als die Hälfte des Halbkugelvolumens beträgt