Aufgabe 1
Gegeben sind das gerade Prisma mit den Eckpunkten , und sowie der Punkt (vgl. Abbildung 1).
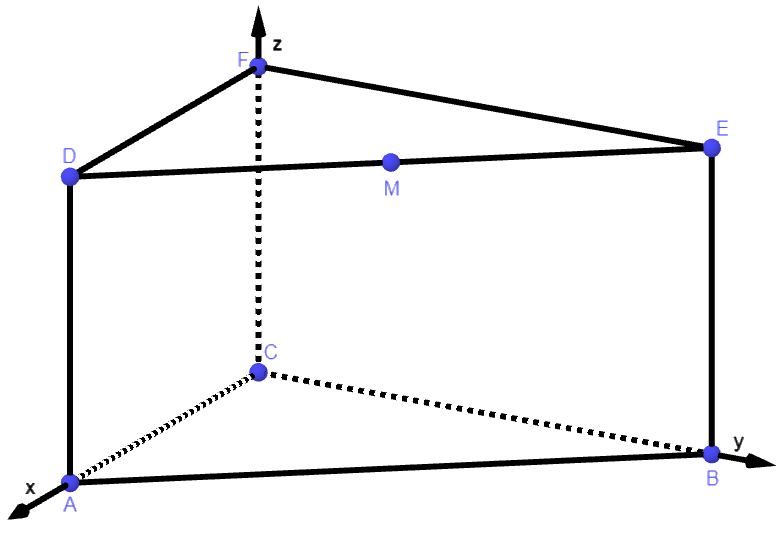
Abbildung 1
Berechnen Sie die Größe des Innenwinkels des Dreiecks bei . (2 P)
Berechnen Sie den Inhalt der Oberfläche des Prismas. (4 P)
Gegeben sind das gerade Prisma mit den Eckpunkten , und sowie der Punkt (vgl. Abbildung 1).

Abbildung 1
Berechnen Sie die Größe des Innenwinkels des Dreiecks bei . (2 P)
Berechnen Sie den Inhalt der Oberfläche des Prismas. (4 P)