Teil B: Vektorielle Geometrie

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 | 0 | 0), D (6 | 0 | 5)$ , $E (0 | 8 | 5)$ und $F (0 | 0 | 5)$ sowie der Punkt $M (3 | 4 | 5)$ (vgl. Abbildung 1).
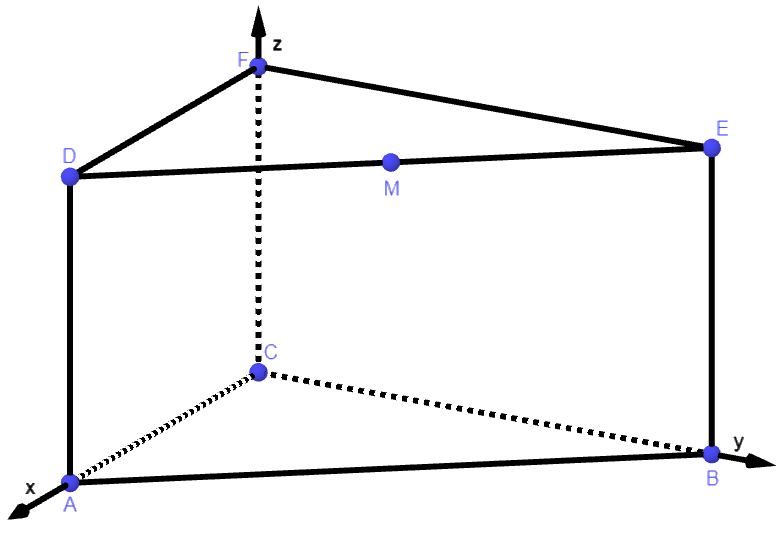
Abbildung 1
1. Berechnen Sie die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
  Berechne die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$
  Mit $α$ wird der Innenwinkel des Dreiecks $D E F$ bei $D$ bezeichnet.
  Dann gilt:
  $\begin{aligned} \cos (α) = \frac{\vec{D E} \circ \vec{D F}}{| \vec{D E} | \cdot | \vec{D F} |} \end{aligned}$
  Berechne die Vektoren und ihre Beträge:
  $\vec{D E} = \vec{O E} - \vec{O D} = (\begin{array}{c} 0 \\ 8 \\ 5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array})$
  $| \vec{D E} | = \sqrt{(- 6)^{2} + 8^{2} + 0} = \sqrt{100} = 10$
  $\vec{D F} = \vec{O F} - \vec{O D} = (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})$
  $| \vec{D F} | = 6$
  Setze die berechneten Größen in den Kosinus ein:
  $\cos (α) = \frac{(\begin{array}{c} - 6 \\ 8 \\ 0 \end{array}) \circ (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})}{10 \cdot 6} = \frac{36}{60} = 0,6$
  $\Rightarrow α = \cos^{- 1} (0,6) \approx {53,13}^{\circ}$
  Die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$ beträgt rund ${53,13}^{\circ}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{D E}$ , $\vec{D F}$ und ihre Beträge.
  Setze in $\begin{aligned} \cos (α) = \frac{\vec{D E} \circ \vec{D F}}{| \vec{D E} | \cdot | \vec{D F} |} \end{aligned}$ ein.
2. Berechnen Sie den Inhalt der Oberfläche des Prismas. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
  Berechne den Inhalt der Oberfläche des Prismas
  Für die Oberflächenberechnung werden verschiedene Vektoren und ihre Beträge benötigt.
  Aus Aufgabe a) folgt:
  $\vec{D E} = (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array})$ , $| \vec{D E} | = 10$
  $\vec{D F} = (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})$ , $| \vec{D F} | = 6$
  Berechne weiter:
  $\begin{array}{l} \vec{F E} = \vec{O E} - \vec{O F} = (\begin{array}{c} 0 \\ 8 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} 0 \\ 8 \\ 0 \end{array}) \\ | \vec{F E} | = 8 \end{array}$
  Die Höhe des Prismas ist $h = 5$ .
  Dann folgt für den Oberflächeninhalt des Prismas:
  $O_{Prisma} = | \vec{D F} | \cdot h + | \vec{E F} | \cdot h + | \vec{D E} | \cdot h + 2 \cdot \frac{1}{2} \cdot | \vec{D F} | \cdot | \vec{E F} |$
  $O_{Prisma} = (6 + 8 + 10) \cdot 5 + 2 \cdot \frac{1}{2} \cdot 6 \cdot 8 = 168$
  Der Inhalt der Oberfläche des Prismas beträgt $168 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Vektor $\vec{F E}$ und seinen Betrag.
  Die Höhe des Prismas ist die z-Koordinate eines in der Deckfläche liegenden Punktes.
  $O_{Prisma} = | \vec{D F} | \cdot h + | \vec{E F} | \cdot h + | \vec{D E} | \cdot h + 2 \cdot \frac{1}{2} \cdot | \vec{D F} | \cdot | \vec{E F} |$
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
In Aufgabe 1 sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 | 0 | 0), D (6 | 0 | 5)$ , $E (0 | 8 | 5)$ und $F (0 | 0 | 5)$ sowie der Punkt $M (3 | 4 | 5)$ gegeben.
Mit $W_{t}$ wird die Ebene bezeichnet, die die Punkte $M, F$ und $S_{t} (t | 0 | 0)$ mit $t \geq 0$ enthält.
In Abbildung 2 ist dieser Sachverhalt für einen bestimmen Wert von $t$ dargestellt.
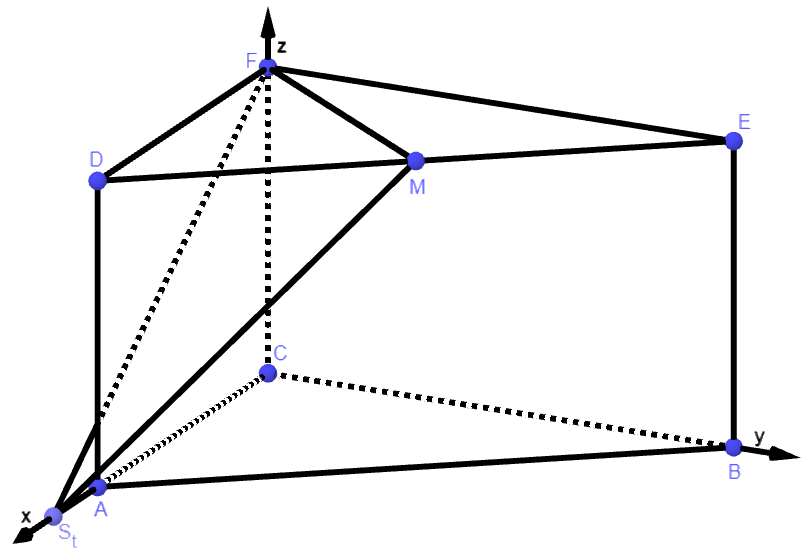
Abbildung 2
1. Stellen Sie eine Gleichung der Ebene $W_{t}$ in Parameterform auf. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten
  Stelle eine Gleichung der Ebene $W_{t}$ in Parameterform auf
  Ebene durch die drei Punkte $F, M$ und $S_{t}$ :
  $W_{t} : \vec{x} = \vec{O F} + r \cdot \vec{F M} + s \cdot \vec{F S_{t}}$
  $\vec{F M} = \vec{O M} - \vec{O F} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} 3 \\ 4 \\ 0 \end{array})$
  $\vec{F S_{t}} = \vec{O S_{t}} - \vec{O F} = (\begin{array}{c} t \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} t \\ 0 \\ - 5 \end{array})$
  Damit folgt:
  $W_{t} : \vec{x} = (\begin{matrix} 0 \\ 0 \\ 5 \end{matrix}) + r \cdot (\begin{matrix} 3 \\ 4 \\ 0 \end{matrix}) + s \cdot (\begin{matrix} t \\ 0 \\ - 5 \end{matrix})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ebene durch die drei Punkte $F, M$ und $S_{t}$ .
  $W_{t} : \vec{x} = \vec{O F} + r \cdot \vec{F M} + s \cdot \vec{F S_{t}}$
2. Bestimmen Sie die Koordinaten eines Normalenvektors der Ebene $W_{t}$ .
  $[$ Zur Kontrolle: $(\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array})$ ist ein Normalenvektor der Ebene $W_{t} .]$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalenvektor – Umwandeln von Ebenendarstellungen
  Bestimme die Koordinaten eines Normalenvektors der Ebene $W_{t}$
  Der Normalenvektor $\vec{n_{W_{t}}} = (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ muss senkrecht auf den beiden Richtungsvektoren stehen $\Rightarrow$ Skalarprodukt ist gleich null.
  $(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) \circ (\begin{array}{c} 3 \\ 4 \\ 0 \end{array}) = 0$ und $(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) \circ (\begin{array}{c} t \\ 0 \\ - 5 \end{array}) = 0$
  Man erhält das Gleichungssystem:
  $\begin{array}{rccccccc} I & 3 \cdot n_{1} & + & 4 \cdot n_{2} & = & 0 \\ II & t \cdot n_{1} & - & 5 \cdot n_{3} & = & 0 \end{array}$
  Aus $I$ folgt: $n_{2} = - \frac{3}{4} n_{1}$ und aus $II$ folgt $t \cdot n_{1} = 5 \cdot n_{3}$ .
  $n_{3}$ ist frei wählbar, z.B. $\Rightarrow n_{3} = 4 \cdot t$
  Damit ist dann $t \cdot n_{1} = 5 \cdot 4 \cdot t \Rightarrow n_{1} = 20$ und $n_{2} = - \frac{3}{4} \cdot 20 = - 15$
  Man erhält als möglichen Normalenvektor von $W_{t} : \vec{n_{W_{t}}} = (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Normalenvektor $\vec{n_{W_{t}}} = (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ muss senkrecht auf den beiden Richtungsvektoren stehen $\Rightarrow$ Skalarprodukt ist gleich null.
3. Berechnen Sie die Größe des Winkels zwischen der Ebene $W_{5}$ und der x-y-Ebene. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
  Berechne die Größe des Winkels zwischen der Ebene $W_{5}$ und der x-y-Ebene
  Für die Ebene $W_{5}$ ist $t = 5$ .
  Der Normalenvektor der Ebene $W_{5}$ ist dann $\vec{n_{W_{5}}} = (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot 5 \end{array}) = (\begin{array}{c} 20 \\ - 15 \\ 20 \end{array})$ .
  $| \vec{n_{W_{5}}} | = \sqrt{20^{2} + (- 15)^{2} + 20^{2}} = \sqrt{1025}$
  Der Normalenvektor der x-y-Ebene ist $\vec{n_{x y}} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ .
  $| \vec{n_{x y}} | = 1$
  Dann gilt für den Winkel:
  $\cos (β) = \frac{| \vec{n_{W_{5}}} \circ \vec{n_{x y}} |}{| \vec{n_{W_{5}}} | \cdot | \vec{n_{x y}} |} = \frac{| (\begin{array}{c} 20 \\ - 15 \\ 20 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) |}{\sqrt{1025} \cdot 1} = \frac{20}{\sqrt{1025}} = \frac{4}{\sqrt{41}}$ $\Rightarrow β = \cos^{- 1} (\frac{4}{\sqrt{41}}) \approx {51,34}^{\circ}$
  Die Größe des Winkels zwischen der Ebene $W_{5}$ und der x-y-Ebene beträgt rund ${51,34}^{\circ}$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Normalenvektor der Ebene $W_{5}$ ist $\vec{n_{W_{5}}} = (\begin{array}{c} 20 \\ - 15 \\ 20 \end{array})$ .
  Der Normalenvektor der x-y-Ebene ist $\vec{n_{x y}} = (\begin{array}{l} 0 \\ 0 \\ 1 \end{array})$ .
  Dann gilt für den Winkel: $\cos (β) = \frac{| \vec{n_{W_{5}}} \circ \vec{n_{x y}} |}{| \vec{n_{W_{5}}} | \cdot | \vec{n_{x y}} |}$
4. Untersuchen Sie, ob es einen Wert von $t$ gibt, für den die Strecke $B D$ senkrecht zur Ebene $W_{t}$ verläuft. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Untersuche, ob es einen Wert von $t$ gibt, für den die Strecke $B D$ senkrecht zur Ebene $W_{t}$ verläuft
  Gegeben ist $\vec{n_{W_{t}}} = (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array})$ und $\vec{B D} = \vec{O D} - \vec{O B} = (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 8 \\ 0 \end{array}) = (\begin{array}{c} 6 \\ - 8 \\ 5 \end{array})$ .
  Dann muss $\vec{n_{W_{t}}} ∥ \vec{B D}$ sein.
  $\Rightarrow$
  $\vec{n_{W_{t}}} = r \cdot \vec{B D} \Leftrightarrow | \begin{array}{ccc} 20 & = & r \cdot 6 \\ - 15 & = & r \cdot (- 8) \\ 4 \cdot t & = & r \cdot 5 \end{array} |$
  Aus Gleichung $I$ folgt $r = \frac{20}{6} = \frac{10}{3}$ .
  Aus Gleichung $II$ folgt $r = \frac{- 15}{- 8} = \frac{15}{8}$ .
  Damit ergibt sich ein Widerspruch da $\frac{10}{3} \neq \frac{15}{8}$ .
  Für keinen Wert von $t$ gibt es eine Lösung des Gleichungssystems.
  Es gibt keinen Wert von $t$ gibt, für den die Strecke $B D$ senkrecht zur Ebene $W_{t}$ verläuft.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Prüfe, ob $\vec{n_{W_{t}}} = r \cdot \vec{B D}$ für einen Wert von $t$ erfüllt ist.
5. Die Gerade $g_{t}$ verläuft durch den Punkt $D$ und senkrecht zur Ebene $W_{t}$ .
  Für $t > 0$ schneidet die Gerade $g_{t}$ die $x$ - $y$ -Ebene im Punkt $Q_{t}$ . Bestimmen Sie die Koordinaten des Punktes $Q_{t}$ .
  $[$ Zur Kontrolle: $Q_{t} (6 - \frac{25}{t} | \frac{75}{4 \cdot t} | 0) .]$ (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Bestimme die Koordinaten des Punktes $Q_{t}$
  Es ist $\vec{O D} = (\begin{array}{c} 6 \\ 0 \\ 5 \end{array})$ und der Richtungsvektor der Geraden $g_{t}$ ist der Normalenvektor $\vec{n_{W_{t}}} = (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array})$ der Ebene $W_{t}$ .
  $g_{t} : \vec{x} = \vec{O D} + r \cdot \vec{n_{W_{t}}} = (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) + r \cdot (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array})$ mit $r \in ℝ$
  Die Gerade $g_{t}$ schneidet die $x$ - $y$ -Ebene, wenn $z = 0$ ist.
  $\Rightarrow 0 = 5 + r \cdot 4 \cdot t \Rightarrow r = - \frac{5}{4 \cdot t}$
  Eingesetzt in die Geradengleichung erhält man
  ${\vec{x}}_{Q_{t}} = (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) - \frac{5}{4 \cdot t} \cdot (\begin{array}{c} 20 \\ - 15 \\ 4 \cdot t \end{array}) = (\begin{array}{c} 6 - \frac{25}{t} \\ \frac{75}{4 \cdot t} \\ 0 \end{array})$
  Damit besitzt der Punkt $Q_{t}$ die Koordinaten $Q_{t} (6 - \frac{25}{t} | \frac{75}{4 \cdot t} | 0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle die Geradengleichung auf $g_{t} : \vec{x} = \vec{O D} + r \cdot \vec{n_{W_{t}}}$ .
  Die Gerade $g_{t}$ schneidet die $x$ - $y$ -Ebene, wenn $z = 0$ ist.
  Löse $z = 0$ nach $r$ auf und setze das erhaltene $r$ in die Geradengleichung ein.
6. Im Folgenden sind drei Schritte der Lösung einer Aufgabe angegeben, die im Zusammenhang mit den betrachteten geometrischen Objekten steht:
  (I) $P (6 - 6 \cdot r | 8 \cdot r | 0)$ mit $0 \leq r \leq 1$ .
  (II) $| \begin{aligned} 6 - \frac{25}{t} & = 6 - 6 \cdot r \\ \frac{75}{4 \cdot t} & = 8 \cdot r \end{aligned} |$ .
  (III) Das Gleichungssystem (II) besitzt keine Lösung.
  Geben Sie eine passende Aufgabenstellung an und interpretieren Sie (III) geometrisch.
  (2P+1P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
  Gib eine passende Aufgabenstellung an
  Gegeben:
  $(I) P (6 - 6 \cdot r | 8 \cdot r | 0)$ mit $0 \leq r \leq 1$
  Es gilt: $\vec{A B} = \vec{O B} - \vec{O A} = (\begin{array}{c} 0 \\ 8 \\ 0 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array})$ und
  $g_{A B} : \vec{x} = \vec{O A} + r \cdot \vec{A B} = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array}) = (\begin{array}{c} 6 - 6 \cdot r \\ 8 \cdot r \\ 0 \end{array})$
  Demnach ist wegen $0 \leq r \leq 1$ der Punkt $P$ ein Punkt, der auf der Stecke $A B$ liegt.
  Weiterhin ist die folgende Gleichung gegeben:
  $(I I) | \begin{aligned} 6 - \frac{25}{t} & = 6 - 6 \cdot r \\ \frac{75}{4 \cdot t} & = 8 \cdot r \end{aligned} |$
  Mit $\vec{O Q_{t}} = (\begin{array}{c} 6 - \frac{25}{t} \\ \frac{75}{4 \cdot t} \\ 0 \end{array})$ und $\vec{O P} = (\begin{array}{c} 6 - 6 \cdot r \\ 8 \cdot r \\ 0 \end{array})$ erhält man die angegebene Gleichung $(I I)$ .
  Eine mögliche Aufgabenstellung lautet:
  Untersuchen Sie, ob es einen Wert von $t$ gibt, für den der Punkt $Q_{t}$ auf der Strecke $A B$ liegt.
  Interpretiere $(I I I)$ geometrisch
  Interpretation von $(I I I)$ : Es gibt keinen Wert von $t$ , für den der Punkt $Q_{t}$ auf der Strecke $A B$ liegt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\vec{A B}$ und $g_{A B}$ . Welche Eigenschaft hat dann der gegebene Punkt $P$ ?
  Welche beiden Vektoren sollen im Gleichungssystem $(I I)$ gleich groß sein?
  Welche Schlussfolgerung kann man aus $(I I I)$ ziehen?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil B: Vektorielle Geometrie

Aufgabe 1

Berechne die Größe des Innenwinkels des Dreiecks DEF bei D

Hast du eine Frage oder Feedback?

Berechne den Inhalt der Oberfläche des Prismas

Hast du eine Frage oder Feedback?

Aufgabe 2

Stelle eine Gleichung der Ebene Wt in Parameterform auf

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten eines Normalenvektors der Ebene Wt

Hast du eine Frage oder Feedback?

Berechne die Größe des Winkels zwischen der Ebene W5 und der x-y-Ebene

Hast du eine Frage oder Feedback?

Untersuche, ob es einen Wert von t gibt, für den die Strecke BD senkrecht zur Ebene Wt verläuft

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten des Punktes Qt

Hast du eine Frage oder Feedback?

Gib eine passende Aufgabenstellung an

Interpretiere (III) geometrisch

Hast du eine Frage oder Feedback?

Berechne die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$

Stelle eine Gleichung der Ebene $W_{t}$ in Parameterform auf

Bestimme die Koordinaten eines Normalenvektors der Ebene $W_{t}$

Berechne die Größe des Winkels zwischen der Ebene $W_{5}$ und der x-y-Ebene

Untersuche, ob es einen Wert von $t$ gibt, für den die Strecke $B D$ senkrecht zur Ebene $W_{t}$ verläuft

Bestimme die Koordinaten des Punktes $Q_{t}$

Interpretiere $(I I I)$ geometrisch