B4 - lernen mit Serlo!

Aufgabe 2

Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.

Die Fahrschulkette plant für das Jahr 2022 die Eröffnung einer Filiale in Soest. Die Zentrale stellt als Anspruch an die Ausbildungsqualität, dass von den praktischen Prüfungen im Schnitt mindestens $70 %$ bestanden werden. Man prognostiziert für Soest, dass $200$ praktische Prüfungen im Jahr 2022 $70 %$ bestanden werden. Wenn davon mindestens $140$ Prüfungen bestanden werden, will die Zentrale davon ausgehen, dass auch in Soest aufgrund der Ausbildungsqualität jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 %$ bestanden wird. Es wird modellhaft angenommen, dass die Anzahl $Y$ der bestandenen Prüfungen unter den $200$ prognostizierten Prüfungen binomialverteilt ist.

Bestimmen Sie die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 %$ bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils $65 %$ bestanden werden. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Bestimme die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 %$ bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils $65 %$ bestanden werden
Berechne $P_{200;\; 0{,}65}(Y\geq 140)=\text{binomCdf(200{,}0.65{,}140{,}200}\approx0{,}0783$ .
Die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 %$ bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils $65 %$ bestanden werden, beträgt rund $0,0783$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $P_{200;\; 0{,}65}(Y\geq 140)$ .
Die Abbildung zeigt das Histogramm zu $P_{200 ; 0{,}7}(Y=k)$ , also für den Fall, dass $p = 0,7$ gilt.
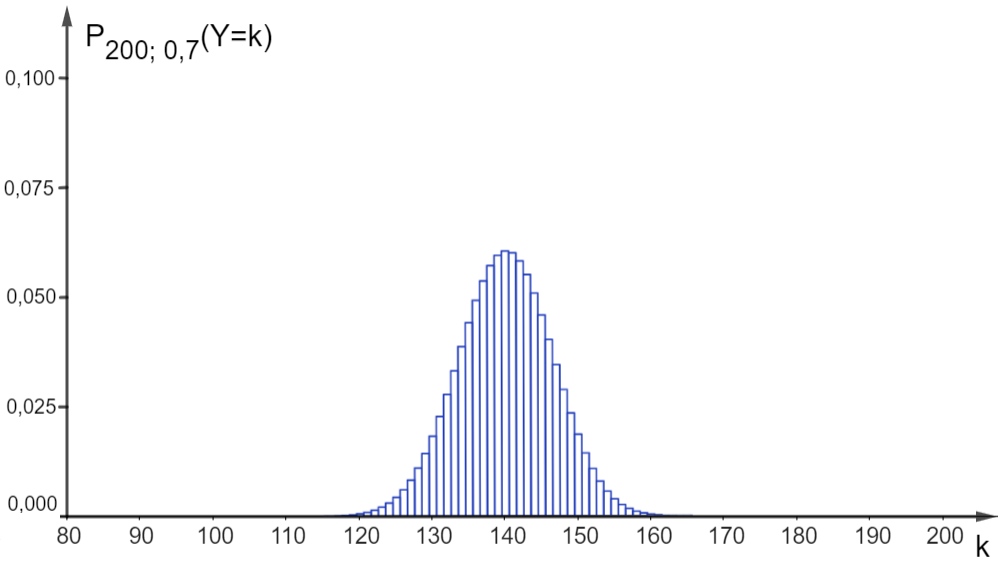
Abbildung
Falls von den $200$ prognostizierten praktischen Prüfungen in Soest z.B. nur $130$ bestanden werden, kommt die Zentrale zu der Einschätzung, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von weniger als $70 %$ bestanden wird.
Erklären Sie mithilfe des Histogramms, warum die Zentrale bei dieser Einschätzung einen Irrtum begangen haben könnte.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Erkläre mithilfe des Histogramms, warum die Zentrale bei dieser Einschätzung einen Irrtum begangen haben könnte
In der Abbildung liegt der Erwartungswert bei $\mu=200\cdot 0{,}7=140$ .
Für $k = 130$ ist die Wahrscheinlichkeit deutlich größer als null.
Beträgt die Bestehungswahrscheinlichkeit $70 %$ , dann sind also auch geringere Erfolgsquoten möglich, ohne dass $p=70\;\%$ als falsch angesehen wird.
Die Zentrale begeht also einen Irrtum, wenn sie von einer geringeren Bestehungswahrscheinlichkeit für eine Prüfung ausgehen würde.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
In der Abbildung liegt der Erwartungswert bei $\mu=200\cdot 0{,}7=140$ .
Für $k = 130$ ist die Wahrscheinlichkeit deutlich größer als null. Was bedeutet das?

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 2

Bestimme die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens 70 %70\;\%70% bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils 65 %65\;\%65% bestanden werden

Hast du eine Frage oder Feedback?

Erkläre mithilfe des Histogramms, warum die Zentrale bei dieser Einschätzung einen Irrtum begangen haben könnte

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 %$ bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils $65 %$ bestanden werden