Das gleichschenklige Dreieck $ABCABC$ und das rechtwinklige Trapez $FBDEFBDE$ überdecken sich teilweise.

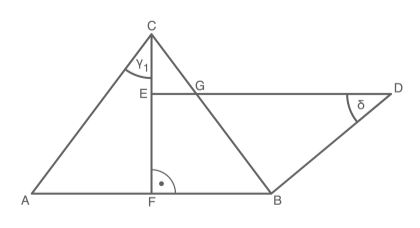
Es gilt:

$\overline{AC}=\mathrm{11,4}\text{ cm}\backslash overline\{AC\}=11\{,\}4\backslash cm$

$\overline{BD}=\mathrm{8,2}\text{ cm}\backslash overline\{BD\}=8\{,\}2\backslash cm$

${\gamma }_1=\mathrm{37,6}\mathrm{°}\backslash gamma\_1=37\{,\}6°$

$\delta =\mathrm{39,2}\mathrm{°}\backslash delta=39\{,\}2°$

$\overline{AC}=\overline{BC}\backslash overline\{AC\}=\backslash overline\{BC\}$

Berechne den Flächeninhalt des Vierecks $FBGEFBGE$.

[5 P]

Eine nach oben geöffnete verschobene Normalparabel $pp$ mit der Form $y=x^2+bx-2y=x^2+bx-2$ geht durch den Punkt $A(1\mathrm{\mid }1)A(1|1)$.

Berechne die Funktionsgleichung der Parabel $pp$.

Die Parabel $pp$ geht auch durch den Punkt $B(-3\mathrm{\mid }{y}_{B}B(-3|y\_B$).

Sie schneidet die $yy$-Achse im Punkt $C\mathrm{.}C.$

Bestimme die Koordinaten der Punkte $BB$ und $CC$.

Die Punkte $A,BA,B$ und $CC$ bilden das Dreieck $ABCABC$.

Berechne den Flächeninhalt des Dreiecks $ABCABC$.

Die Gerade $gg$ geht durch den Punkt $CC$ und hat die Steigung $m=-3m=-3$ .

Gib die Funktionsgleichung von $gg$ an.

Julius behauptet: „Die Gerade $gg$ halbiert den Flächeninhalt des Dreiecks $ABCABC$".

Überprüfe diese Aussage und begründe deine Antwort durch Rechnung oder Argumentation.

[ 5 P ]