1 Übersicht
Inhalt des Kurses
Du kannst bereits mit dem Prozentzeichen umgehen und in verschiedenen Situationen Prozentrechnungen durchführen. Ziel dieses Kurses ist es, dein Wissen über Prozentrechnung zu vertiefen und in komplexeren Alltagssituationen anzuwenden. Im Folgenden werden dir drei Darstellungsformen von Prozentangaben vorgestellt. Außerdem erhältst du eine Einführung in die Zinsrechnung.
Vorkenntnisse
Du solltest den Kurs Einführung des Prozentzeichens und seiner Umrechnung bereits verstanden haben.
Der Anwendungskurs baut unmittelbar auf den Kursen Einführung in Grundwert, Prozentwert und Prozentsatz und Einführung in den verminderten und vermehrten Grundwert auf. Dort begegnest du dem Prozentrechnen mit Grundwert, Prozentwert und Prozentsatz. Außerdem lernst du das Konzept des verminderten und vermehrten Grundwerts kennen.
Kursdauer
ungefähr 2-3 Stunden (wenn du alle Aufgaben selbstständig lösen möchtest)
2 Anwendungen im Alltag
Wenn Wahlergebnisse im Fernsehen präsentiert werden, werden die Prozentangaben oft in Säulen- oder Kreisdiagrammen dargestellt. Auch für Umfragen und Statistiken werden solche Diagramme verwendet.
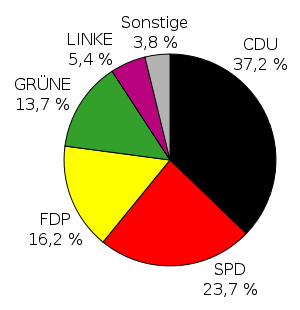
Wahlergebnis der Landtagswahl in Hessen von 2009
Banken, Möbelgeschäfte oder auch Elektronikhändler werben oft mit Aussagen wie " Finanzierung" oder "nur Zinsen". Zinsrechnung ist ein bekanntes und wichtiges Anwendungsbeispiel der Prozentrechnung.


3 Diagramme als Darstellungsform für Prozentzahlen
Dir sind im Alltag sicher schon verschiedene Diagramme begegnet. Diagramme dienen allgemein dazu, Informationen zu veranschaulichen und es so dem Leser einfacher zu machen, sie zu verstehen.
Im Folgenden werden dir die drei bekanntesten Diagramme vorgestellt.
Kreisdiagramm
Das Kreisdiagramm wird auch Kuchen- oder Tortendiagramm genannt.
Es wird meistens verwendet, um Anteile darzustellen. Der ganze Kreis entspricht dabei dem Grundwert. Prozentuale Anteile des Grundwerts werden mithilfe entsprechend großer Kreissektoren dargestellt.

Säulendiagramm
Jedes Säulendiagramm hat zwei Achsen als Grundgerüst. Auf der waagrechten Achse sind die konkreten Kategorien (z.B. Schüler, Sportarten, Würfelergebnisse, …) abgetragen. Auf der senkrechten Achse sind Prozentzahlen angegeben.
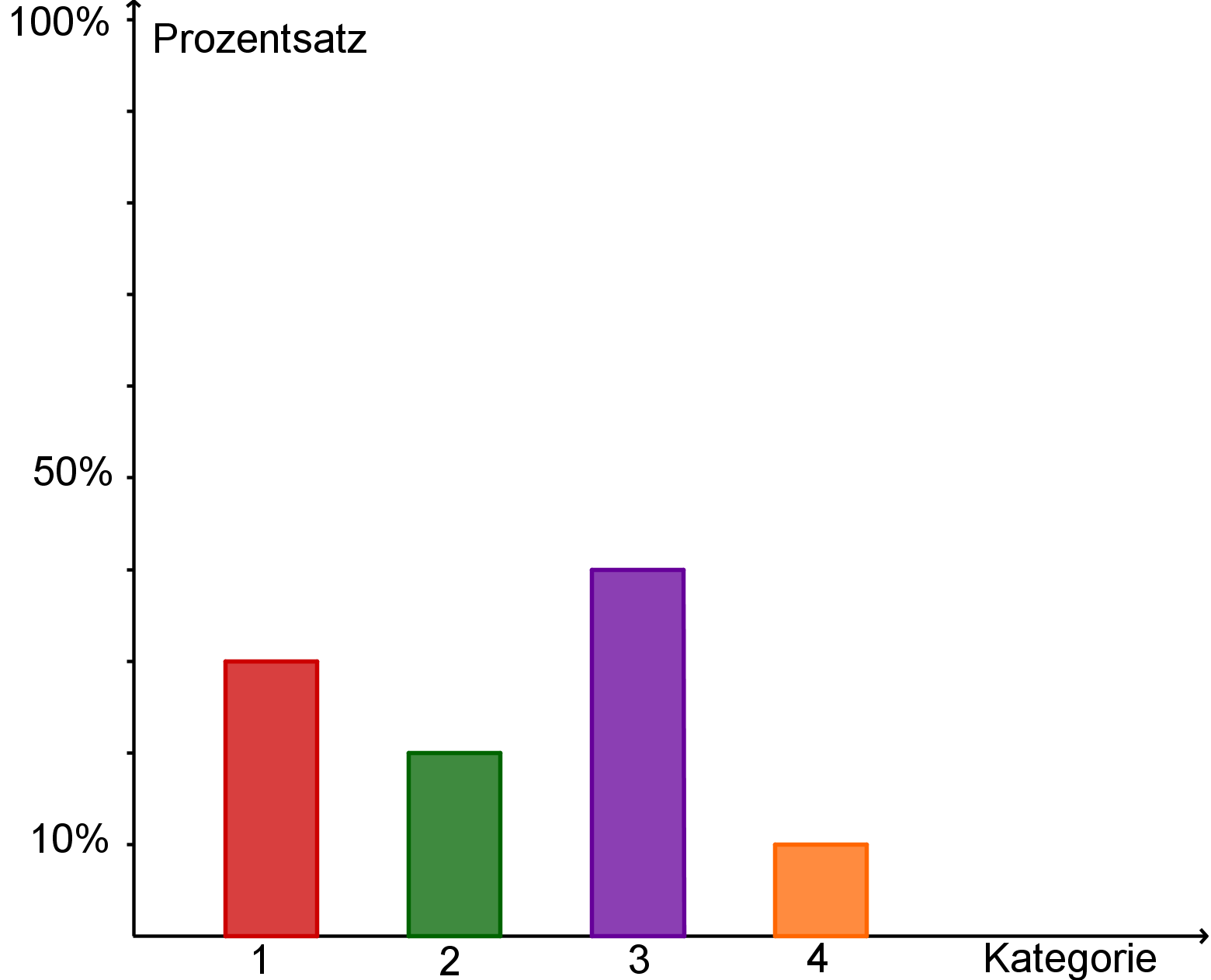
Um die Prozentzahlen den Kategorien zuzuordnen, werden Säulen mit entsprechender Höhe eingezeichnet.
Balkendiagramm
Ein Balkendiagramm ist ein um 90 Grad gedrehtes Säulendiagramm.
Das heißt, auf der waagrechten Achse sind Prozentzahlen abgetragen und auf der senkrechten Achse die Kategorien.
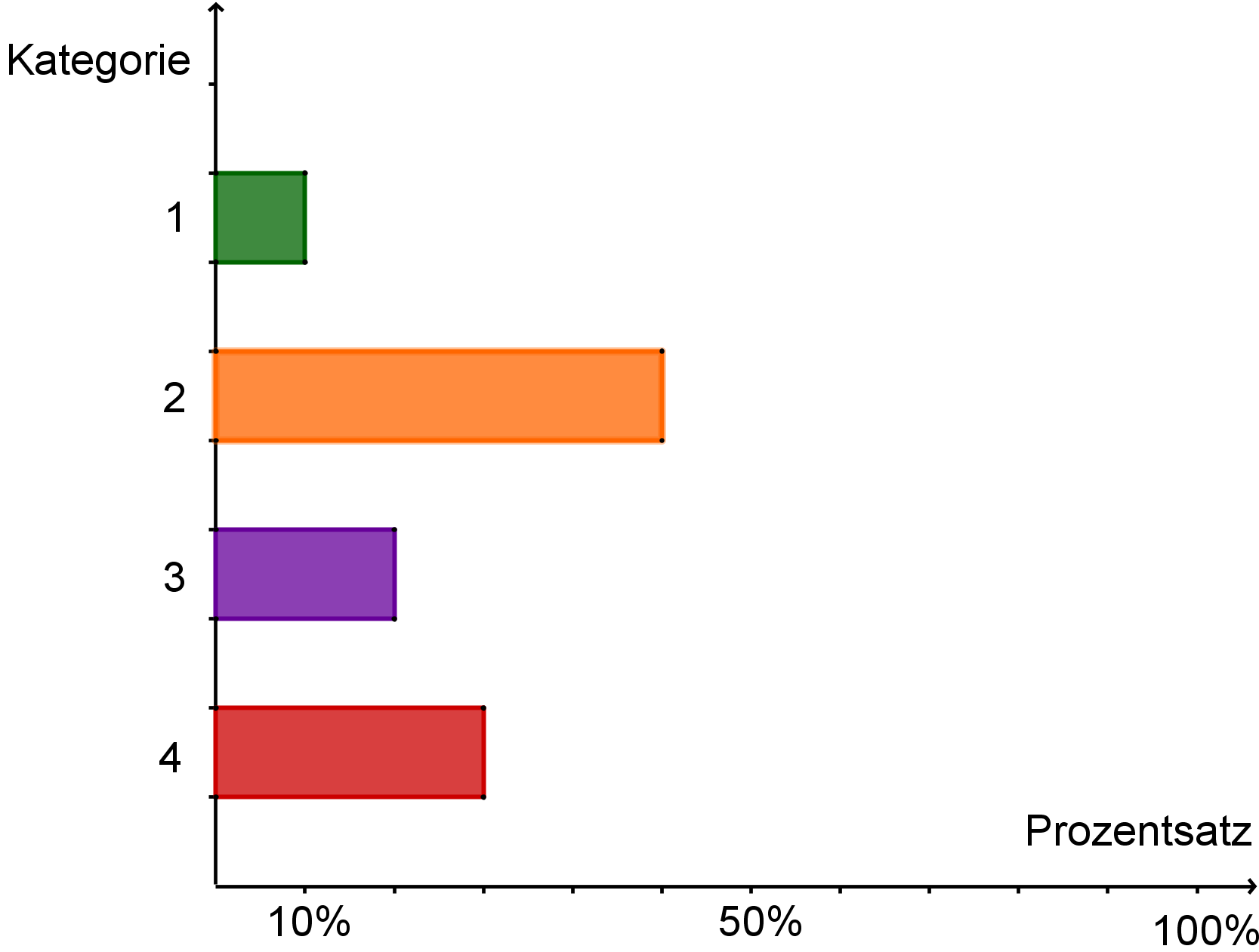
4 Kreisdiagramm
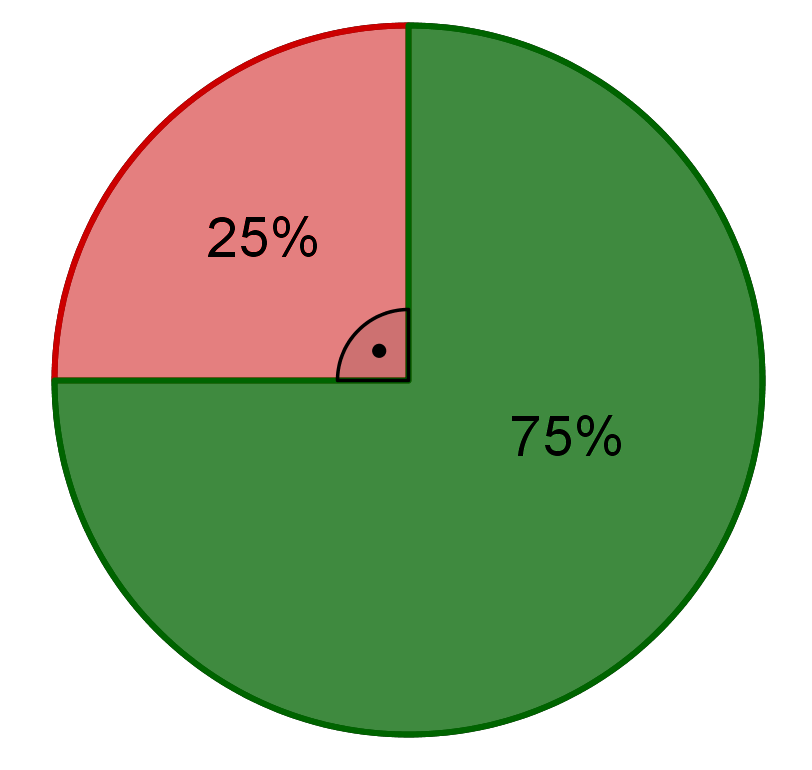
Ein Kreisdiagramm ist ein Kreis, der in verschiedene Kreissektoren aufgeteilt ist. Der Kreis kann in zwei oder mehr Kreissektoren aufgeteilt werden, welche nicht gleich groß sein müssen. entsprechen dem ganzen Kreis, also . Zum Beispiel entsprechen einem Viertelkreis und somit .
Um also Prozentsätze in einem Kreisdiagramm darzustellen, rechnest du entweder mit der Prozentformel oder mit dem Dreisatz die entsprechenden Winkelgrößen aus.
Beispielaufgabe
Für die siebten Klassen der Joseph-Effner-Schule steht demnächst die Wahl des Zweiges an. Die Schule bietet einen sprachlichen und einen naturwissenschaftlichen Zweig an. Auf einer Informationsveranstaltung sagt der Direktor, dass sich letztes Jahr des Jahrgangs für die zusätzliche Sprache und für die Naturwissenschaften entschieden hatten. Stelle diese Verteilung in einem Kreisdiagramm dar.
Berechnung mit der Prozentformel
Du überlegst dir als erstes, welche Größen du gegeben hast und zu welchen Fachbegriffen der Prozentrechnung diese passen. Die Prozentsätze sind sowohl für den sprachlichen als auch den naturwissenschaftlichen Zweig angegeben und der Grundwert entspricht dem ganzen Kreis, also .
Gegeben:
Gesucht sind die Gradzahlen für den sprachlichen (S) und den naturwissenschaftlichen (N) Zweig, also die Prozentwerte.
Gesucht:
Verwende die Prozentformel .
Der Kreissektor des sprachlichen Zweiges hat einen Winkel von , der des naturwissenschaftlichen Zweiges beträgt .
Antwort:

Berechnung mit Dreisatz
Als Erstes wird hier der Kreissektor bzw. die Gradzahl des sprachlichen Zweiges berechnet.
Wie oben schon erwähnt, entspricht dem ganzen Kreis, also . Rechne zuerst auf ein Prozent herunter und dann wieder hoch auf den gesuchten Prozentsatz ().
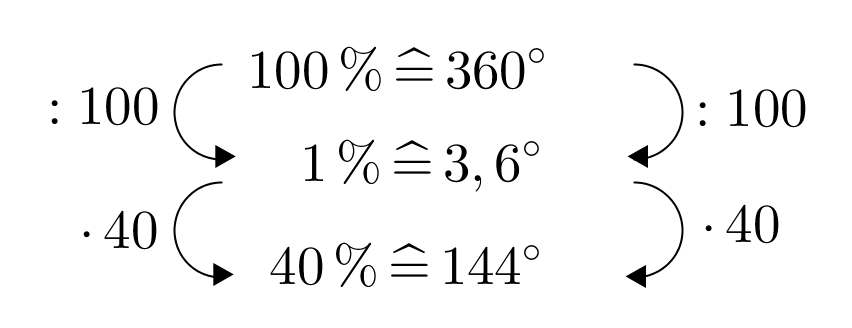
Merke: allgemein gilt , wenn du einen ganzen Kreis als Grundwert betrachtest.
Im Prinzip kannst du mit dem gleichen Vorgehen auch die Gradanzahl für den naturwissenschaftlichen Zweig berechnen.
Da aber die Anzahl der Schüler*innen des sprachlichen und des naturwissenschaftlichen Zweiges zusammen den ganzen Jahrgang ergeben, müssen auch die beiden dazugehörigen Gradzahlen zusammen bilden.
Gradzahl für den naturwissenschaftlichen Zweig:
Der Kreissektor des sprachlichen Zweiges hat einen Winkel von und der des naturwissenschaftlichen Zweiges einen Winkel von .
Antwort: Siehe Beispiel oben
5 Übungsaufgaben zum Kreisdiagramm
Laden
Laden
6 Säulendiagramm
Auf der waagrechten Achse werden bei einem Säulendiagramm immer die Kategorien abgetragen. Auf der senkrechten Achse gibt es allerdings mehrere Möglichkeiten. Man kann einerseits die konkreten Größen einer Einheit (z.B. cm, Schüler, Äpfel, …) oder andererseits Prozentsätze angeben. Dies macht man vor allem dann, wenn es eher um den Vergleich der Größen als um die absoluten Größen geht.
Oft werden z.B. Wahlergebnisse in einem Säulendiagramm dargestellt.
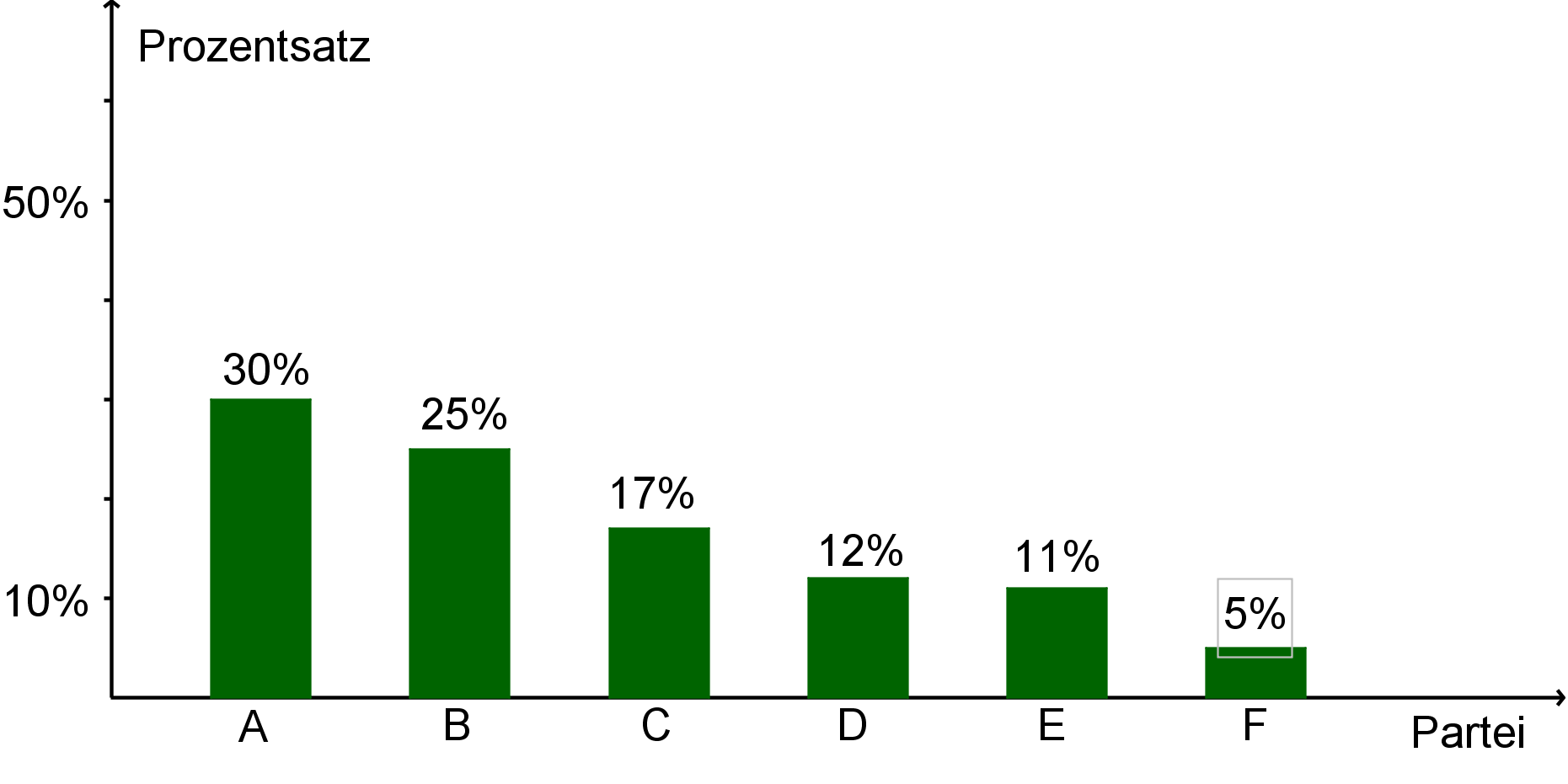
Beispielaufgabe
Auf der Straße wird eine Umfrage nach der Lieblingseissorte gestartet. Die Umfrage ergab Folgendes:
Vanille:
Schokolade:
Erdbeere:
Stracciatella:
Cookies:
Sonstige:

Stelle das Ergebnis in einem Säulendiagramm dar. Auf der senkrechten Achse sollen die Prozentsätze abgetragen werden.
Lösung:
Auf der waagrechten Achse trägst du die Eissorten ein und auf der senkrechten Achse den Prozentsatz. Jeder Eissorte wird eine Säule zugeordnet. Die Höhe der Säulen musst du entsprechend der Prozentsätze auf der senkrechten Achse einzeichnen.
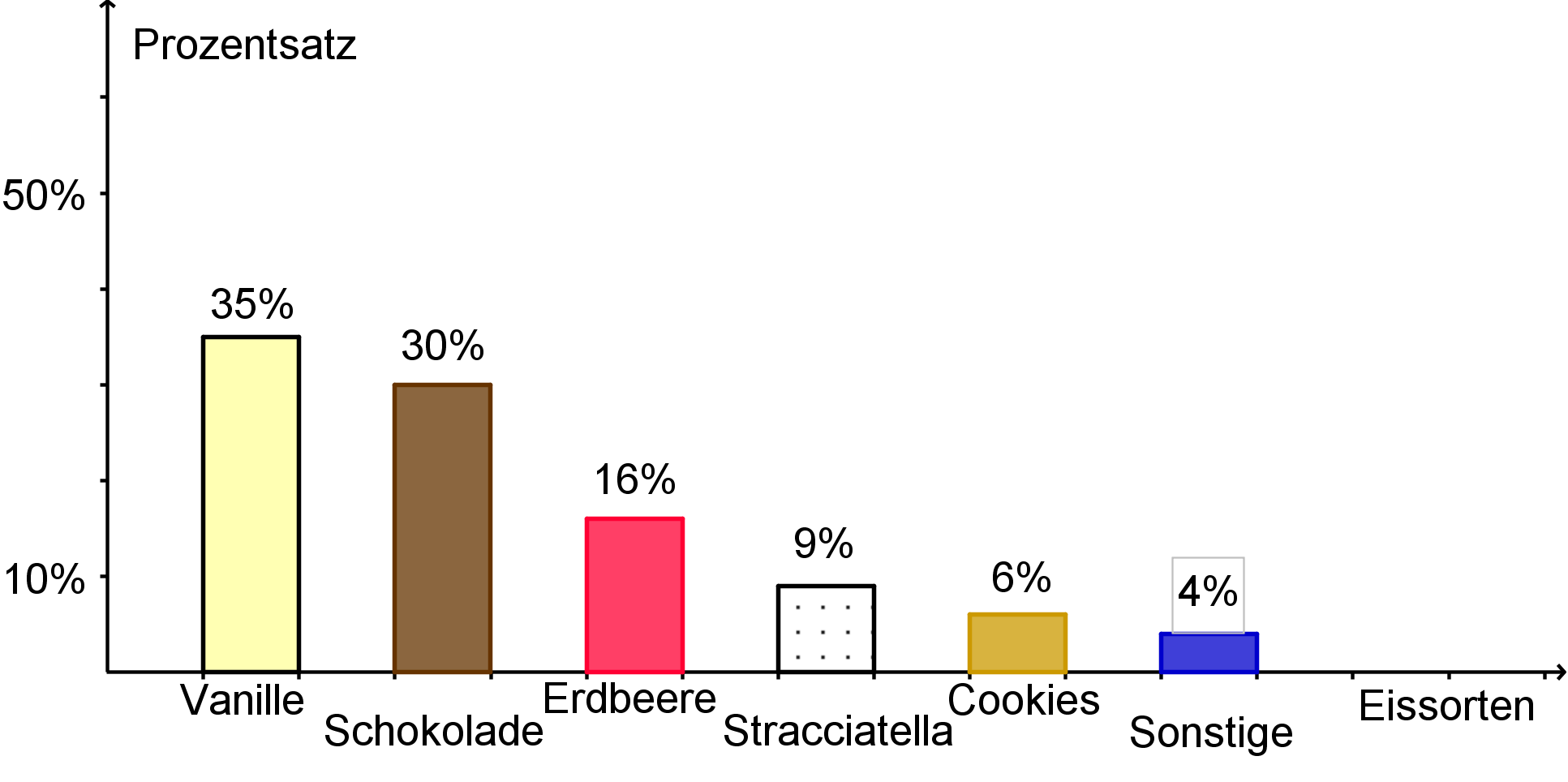
7 Übungsaufgaben zum Säulendiagramm
Laden
Laden
8 Zinsrechnung
Wenn du Geld auf die Bank bringst, erhältst du dafür Zinsen: Das ist ein kleiner Geldbetrag, den die Bank dir dafür zahlt, dass du ihr das Geld leihst. Die Zinsen sind umso höher, je mehr Geld du eingezahlt hast. Die Höhe der Zinsen berechnet die Bank mithilfe eines festgelegten Prozentsatzes, des sogenannten Zinssatzes. Der Zinssatz bezieht sich meistens auf ein Jahr und die so entstehenden Zinsen werden als Jahreszinsen bezeichnet. Das Geld, das du auf die Bank gebracht hast, ist der Grundwert und wird als Kapital bezeichnet.
Hier handelt es sich also um eine Anwendung der Prozentrechnung. Die Begriffe Prozentwert, Prozentsatz und Grundwert werden dabei anders genannt, da sie sich im Gegensatz zur Prozentrechnung ausschließlich auf Geldbeträge beziehen.
Prozentwert | Prozentsatz | Grundwert | |
|---|---|---|---|
Zinsen | Zinssatz | Kapital | |
Beispiel 1
Du zahlst auf dein Konto ein und erhältst darauf Zinsen pro Jahr. Wie viel Geld hast du nach einem Jahr?
Gegeben: Kapital Zinssatz
Gesucht: Jahreszinsen

Berechnung mit Formel
Berechnung mit Dreisatz
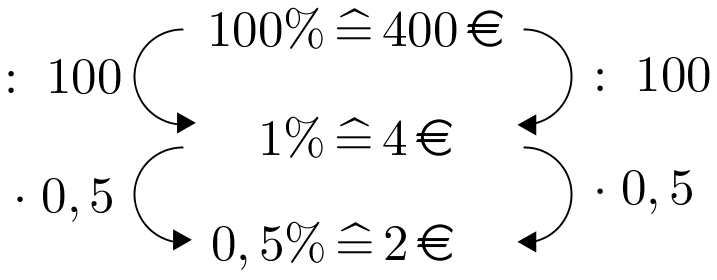
Nach einem Jahr sind auf deinem Konto somit € und zusätzlich € Zinsen. Auf deinem Konto befinden sich folglich €.
Beispiel 2
Nicht nur, wenn du Geld auf der Bank hast, sondern auch, wenn du dir von der Bank (oder jemand anderem) Geld leihst, kann von Zinsrechnung gesprochen werden.
Stell dir vor, du leihst dir von der Bank und die Bank setzt einen Zinssatz von fest. Nach einem Jahr schuldest du der Bank das Kapital von und zusätzlich Zinsen. Diese sind dann ein vermehrter Grundwert / vermehrtes Kapital.
Berechnung mit Formel | Berechnung mit Dreisatz |
|---|---|
Die Zinsen nach einem Jahr betragen also . | 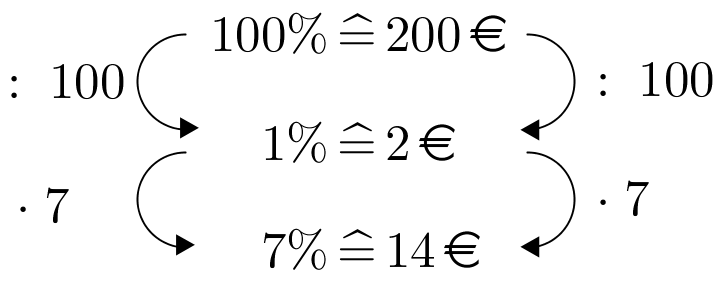 |

Du schuldest der Bank somit .
9 Übungsaufgaben zur Zinsrechnung
Laden
Laden
Laden
10 Zinseszins
Zinsen beziehen sich zwar meist auf ein Jahr, aber was passiert mit Geld, das mehrere Jahre verzinst wird? Sind die Zinserträge jedes Jahr gleich groß, wächst oder schrumpft der Zinsbetrag, den du jedes Jahr bekommst?
Betrachte dazu ein Beispiel
Überlege dir anhand von Startkapital mit Zinsen pro Jahr, wie viel Geld du nach zwei Jahren besitzt.
Drei Lösungswege:
Variante 1 | Variante 2 | Variante 3 |
|---|---|---|
Du erhältst Zinsen auf dein Kapital von .
| Dein Kapital von ist der Grundwert und entspricht somit . | Nach einem Jahr hast du dein Kapital von und zusätzlich deines Kapitals. Da dein Kapital der Grundwert ist, entspricht es . Nach einem Jahr hast du folglich deines Ausgangskapitals. Der Wachstumsfaktor beträgt also .
|
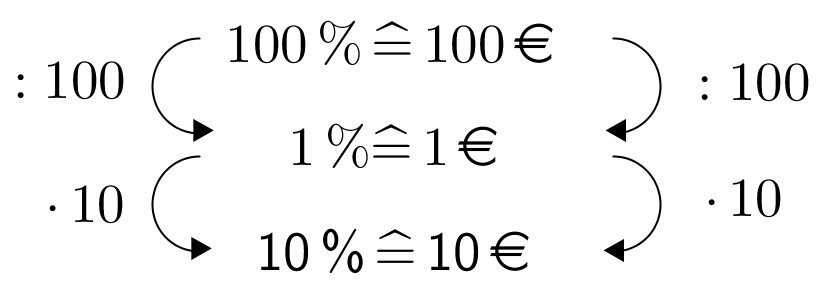 | ||
Nach einem Jahr erhältst du somit Zinsen. Dein neues Kapital beträgt . | Nach einem Jahr erhältst du somit Zinsen. Dein neues Kapital beträgt . | Nach einem Jahr hast du also . Deine Zinsen betragen |
Im zweiten Jahr bekommst du wieder Zinsen auf dein Kapital. Dein Kapital beträgt aber inzwischen €. Du hast also einen neuen Grundwert.
Variante 1 | Variante 2 | Variante 3 |
|---|---|---|
| 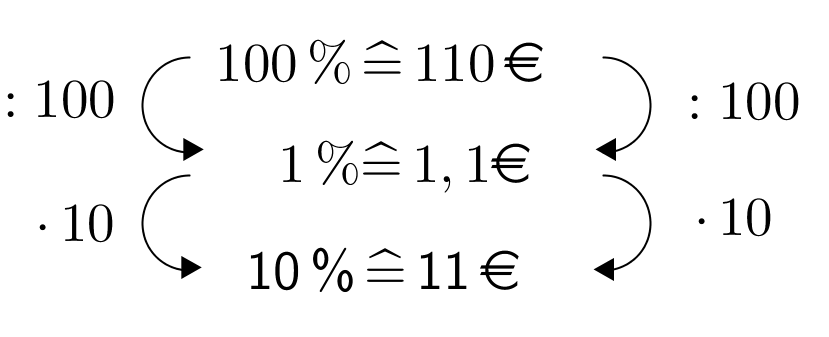 |
|
Für das zweite Jahr erhältst du € Zinsen. Gesamt bekommst du somit Zinsen. | Für das zweite Jahr erhältst du € Zinsen. Gesamt bekommst du somit Zinsen. | Nach zwei Jahren hast du €. Gesamt bekommst du somit Zinsen. |
Fazit:
Würdest du nach zwei Jahren doppelt so viele Zinsen haben wie nach einem Jahr, hättest du . In Wirklichkeit erhältst du aber . Das liegt daran, dass du auf deine Zinsen auch Zinsen bekommst. Diese nennt man Zinseszinsen.
Tipp zur Berechnung des Kapitals nach mehreren Jahren
Der schnellste Weg, das neue Kapital nach einem, zwei oder drei Jahren zu berechnen ist der einschrittige Weg aus der dritten Variante.
Dieses Verfahren kann auch leicht auf drei und vier Jahre erweitert werden.
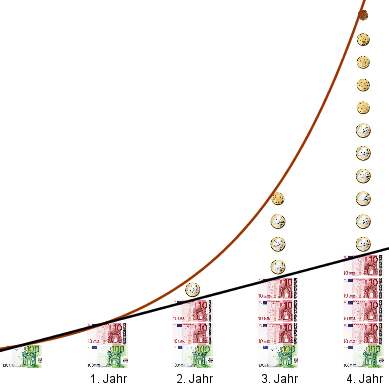
Die Gerade stellt die Geldentwicklung ohne Zinseszins dar. Mit Zinseszins steigen die Zinsen nicht mehr direkt proportional zu der Anzahl an Jahren.
11 Übungsaufgaben zum Zinseszins
Laden
Laden
12 Das Bankjahr
In der Realität werden Geldbeträge nicht immer für ganze Jahre angelegt. Wie werden die Zinsen auf einem Konto berechnet, wenn es innerhalb eines Jahres aufgelöst wird?
Es wäre sehr aufwändig, dafür eine volle Zinsberechnung mit Berücksichtigung des Zinseszinses tagesgenau durchzuführen. In Deutschland wird deshalb meist mit dem Bankjahr gerechnet: Ein Bankjahr hat 360 Tage und besteht aus zwölf Bankmonaten mit jeweils 30 Tagen.
Die bereits vergangene Zeit innerhalb eines Jahres wird zur Zinsberechnung herangezogen. Der Anteil der vergangenen Zeit entspricht dem Anteil der Jahreszinsen, die ausgezahlt werden.
Die Formel zur Zinsberechnung innerhalb eines Jahres für Tage lautet also bei einem Jahreszinssatz von und einem Kapital von :

Beispiel
Ein Konto wird nach 4 Monaten und 18 Tagen aufgelöst. Auf dem Konto lagen zu Zinsen. Wie viele Zinsen werden ausgezahlt?
4 Monate und 18 Tage entsprechen Tagen.
Berechnung mit Formel | Berechnung mit Dreisatz |
|---|---|
| Zunächst müssen die Zinsen für ein ganzes Jahr berechnet werden. |
 | |
Im Anschluss werden die Zinsen berechnet, die ausgezahlt werden. | |
|  |
Bei einer Kontoauflösung nach 4 Monaten und 18 Tagen werden somit zusätzlich zum angelegten Kapital Zinsen ausgezahlt.
Übungsaufgaben
Laden
Laden
13 Prozentpunkte
Sowohl in der Prozent- als auch in der Zinsrechnung kommt es oft vor, dass sich Prozentsätze ändern. Die Änderung wird oft nicht in Prozent, sondern in Prozentpunkten angegeben. Ein Beispiel dafür ist auf dem folgenden Ausschnitt eines Kontoauszugs zu sehen.

Wenn sich ein Prozentsatz ändert, kannst du die Größe der Änderung in Prozent oder in Prozentpunkten angeben.
Bildest du einfach die Differenz der beiden Prozentsätze, so erhältst du die Änderung in Prozentpunkten (nicht in Prozent!).
Wenn du diese Differenz wiederum selbst als Prozentsatz ausdrückst, (d. h. du verwendest den ursprünglichen Wert des Prozentsatzes als Grundwert und den neuen Prozentsatz als Prozentwert), erhältst du die Änderung in Prozent. Die Änderung in Prozent kann also nicht direkt als Differenz abgelesen werden, sondern muss berechnet werden.
Beispiel
Eine Partei bekommt bei einer Wahl der gültigen Stimmen. Bei der nächsten Wahl sind es .
Dies entspricht einer Steigerung
um 4 Prozentpunkte (denn ),
aber
um 50 Prozent (denn: ist hier der Grundwert, ist der Prozentwert. Also haben wir eine Steigerung von: )
Laden
Übungsaufgaben
Laden
Laden
Laden
14 Zusammenfassung
Darstellungsmöglichkeiten von Prozentangaben
Kreisdiagramm (Kuchen- und Tortendiagramm)
In einem Kreisdiagramm sind die prozentualen Anteile einer Grundmenge angegeben. Wenn du ein Kreisdiagramm zeichnest, ist der Grundwert der ganze Kreis, also .

Säulendiagramm
Ein Säulendiagramm hat als Grundgerüst eine waagrechte Achse und eine senkrechte Achse. Bei der waagrechten Achse sind nur die positiven Werte abgetragen. Die Säulen können sowohl absolute als auch relative Werte repräsentieren. Jede Säule steht für eine Kategorie.

Balkendiagramm
Dies ist ein um gedrehtes Säulendiagramm.
Zinsrechnung
Die Zinsrechnung ist eine Anwendung der Prozentrechnung:
Du kannst also mit den dir bekannten Formeln rechnen, sie haben nur andere Bezeichnungen.
Zinseszins
Legt man Geld für mehrere Jahre an, so erhält man ab dem zweiten Jahr Zinsen auch auf die bisherigen Zinserträge.
Das Bankjahr
Das Bankjahr wird benutzt, um Zinsen innerhalb eines Zinszeitraumes zu berechnen. Es besteht aus 360 Tagen. Der Anteil des vergangenen Zeitraumes entspricht dem Anteil der bisherigen Zinsen.
Prozentpunkte
Wenn sich ein Prozentsatz ändert, kannst du die Größe der Änderung in Prozentpunkten angeben. Dazu bildest du die Differenz aus den zwei Prozentsätzen.
15 Zeig, was du kannst!
Laden
Laden
Laden
Laden
Hier findest du weitere Vertiefungsaufgaben zur Prozentrechnung und Aufgaben zur Zinsrechnung.
