Vertiefung zum Kreissektor

Ein Kreissektor ist eine Teilfläche des Kreises, die von einem Kreisbogen und zwei daran angrenzenden Strecken zum Mittelpunkt gebildet wird.

Anschaulich sieht ein Kreissektor aus wie ein Käsestück von oben betrachtet.

Flächenberechnung

Es gibt zwei verschiedene Möglichkeiten, die Fläche eines Kreissektors zu berechnen:

Mit Radius und Mittelpunktswinkel
Mit Radius und Länge des Kreisbogens

Berechnung mit Radius und Mittelpunktswinkel

Die Fläche des Kreissektors ist ein Teil der Kreisfläche. Das Verhältnis zwischen den Flächeninhalten des Kreises und des Kreissektors entspricht dem Verhältnis zwischen Mittelpunktswinkel $\alpha$ und dem Gesamtwinkel mit $360°$ .

Beschreibung	Berechnung
Man stellt die Formel nach $A_{\text{Sektor}}$ um.	$\frac{\alpha}{360°}=\frac{A_{\text{Sektor}}}{A_{\text{Kreis}}}$
Die Fläche eines Kreises ist $A_{\text{Kreis}}=\pi r^2$ .	$A_{\text{Sektor}}=\dfrac{\alpha}{360°}\cdot A_{\text{Kreis}}$
	$A_{\text{Sektor}}=\dfrac{\alpha}{360°}\cdot \pi r^2$

Beispiel

Es soll nun der Flächeninhalt des folgenden Kreissektors (rot) bestimmt werden:

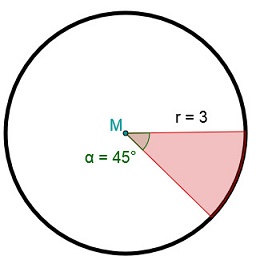
Beschreibung	Berechnung
Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen.	$A=r^2\cdot\mathrm\pi\cdot\frac\alpha{360^\circ}$
	$A=r^2\cdot\mathrm\pi\cdot\frac\alpha{360^\circ} \\ \phantom{h}=3^2\cdot\mathrm\pi\cdot\frac{45^\circ}{360^\circ}\\ \phantom{A} =\;9\cdot\mathrm\pi\cdot\frac18\\ \phantom{A}\approx 3{,}53$

Berechnung mit Radius und Länge des Kreisbogens

Das Verhältnis zwischen dem Umfang $U$ des Kreises und der Länge $b$ des Kreisbogens entspricht dem Verhältnis zwischen den Flächeninhalten des Kreises und des Sektors.

Beschreibung	Berechnung
Man stellt die Gleichung nach $A_{\text{Sektor}}$ um.	$\dfrac{b}{U}=\dfrac{A_{\text{Sektor}}}{A_{\text{Kreis}}}$
Man setzt die Formeln für den Umfang und die Fläche des Kreises ein.	$A_{\text{Sektor}}=\dfrac{b}{U}\cdot A_{\text{Kreis}}$
Im Bruch lässt sich $\pi$ und $r$ kürzen.	$A_{\text{Sektor}}=\dfrac{b}{2\pi r}\cdot \pi r^2$
	$A_{\text{Sektor}}=\dfrac{b \cdot r}{2}$

Beispiel

Es soll nun der Flächeninhalt des folgenden Kreissektors (rot) bestimmt werden:

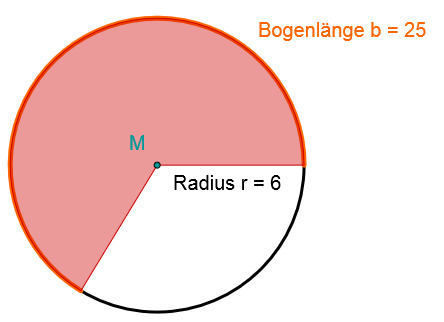
Beschreibung	Berechnung
Setze die Bogenlänge und den Radius in die Formel ein, um den Flächeninhalt zu bestimmen.	$\displaystyle A_\text{Sektor}=\frac{b\cdot r}2$
	$\displaystyle A_\text{Sektor}=\frac{b\cdot r}2=\:\frac{25\cdot6}2=\;75$

Übungsaufgaben: Vertiefung zum Kreissektor

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreise und Kreisteilen

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Videos

Kreissektor, Kreisbogen, Kreissegment

Quellen

Abb. 1: Autor: G. Anfossi, Quelle: Wikimedia Commons

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?