Berechne die Länge der Strecke mithilfe der angegebenen Koordinaten
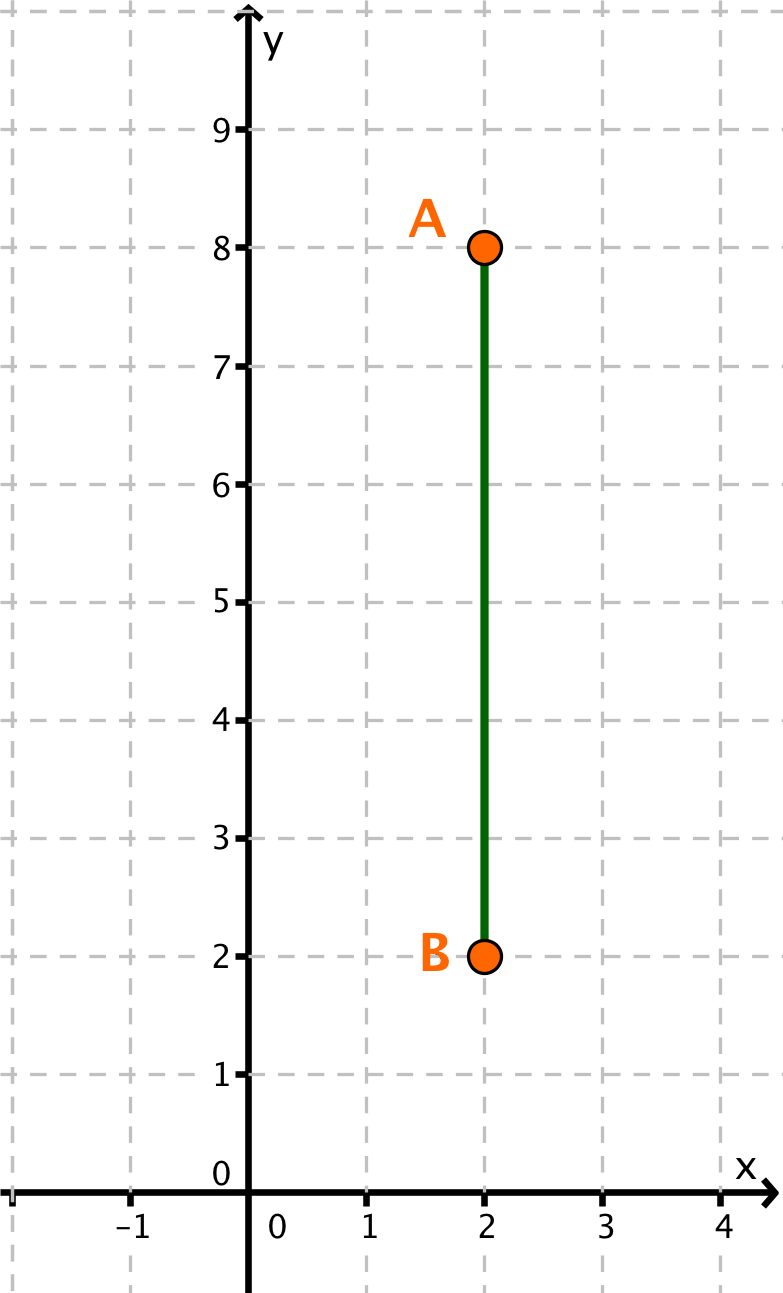
A(2|8), B(2|2)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die gegebenen Punkte in ein Koordinatensystem ein.
Der Punkt A liegt höher als der Punkt B. Außerdem ist die Strecke [AB] parallel zur y-Achse, weil die Punkte A und B den gleichen x-Wert (Rechtswert) haben.
Berechne die Länge der Strecke [AB], indem du den y-Wert des unteren Punktes von dem y-Wert des oberen Punktes subtrahierst.
Setze nun die y-Koordinaten von A und B ein.
Antwort: die Strecke [AB] hat die Länge 6.
Hast du eine Frage oder Feedback?
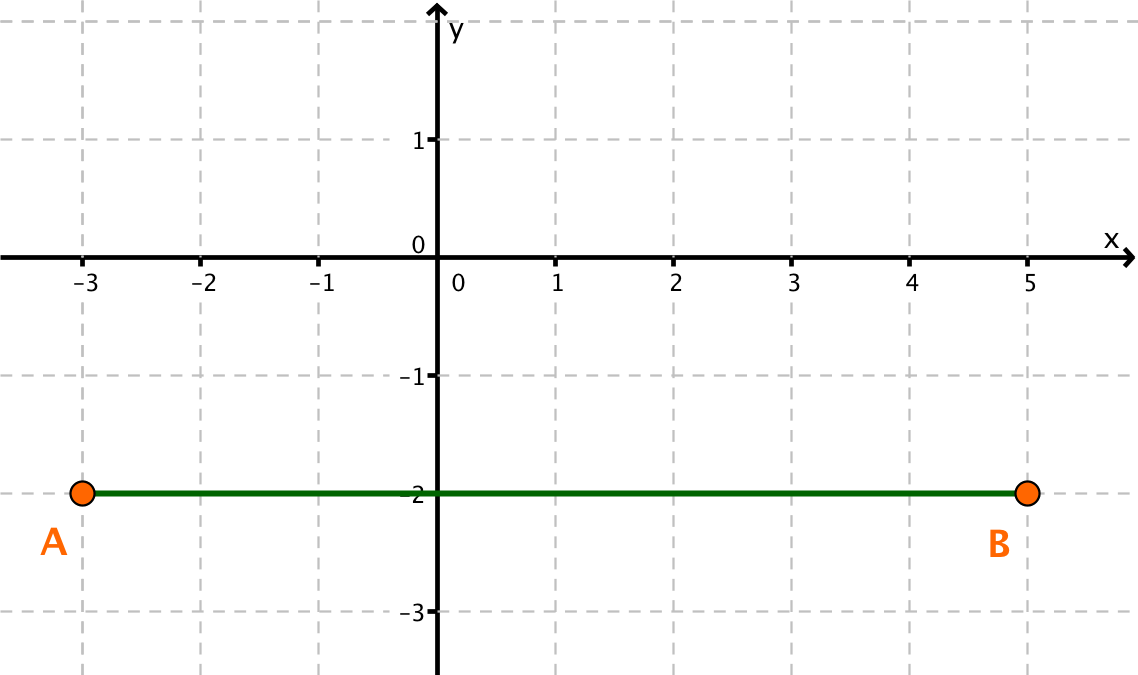
A(-3|-2), B(5|-2)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die Punkte A und B in ein Koordinatensystem ein.
Der Punkt B liegt rechts von dem Punkt A. Außerdem ist die Strecke [AB] parallel zur x-Achse, da die beiden Punkte den gleichen y-Wert (Hochwert) haben.
Berechne die Länge der Strecke [AB], indem du den x-Wert des Punktes, der weiter links liegt (), von dem x-Wert des Punktes, der weiter rechts liegt (), subtrahierst.
Setze die gegebenen x-Werte ein.
Antwort: Die Strecke [AB] hat die Länge 8.
Hast du eine Frage oder Feedback?
A(-2|3), B(1|-1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die Punkte in ein Koordinatensystem ein.
Berechne die Länge der Katheten. Die Kathete 1 ist parallel zur x-Achse und die Kathete 2 ist parallel zur y-Achse.
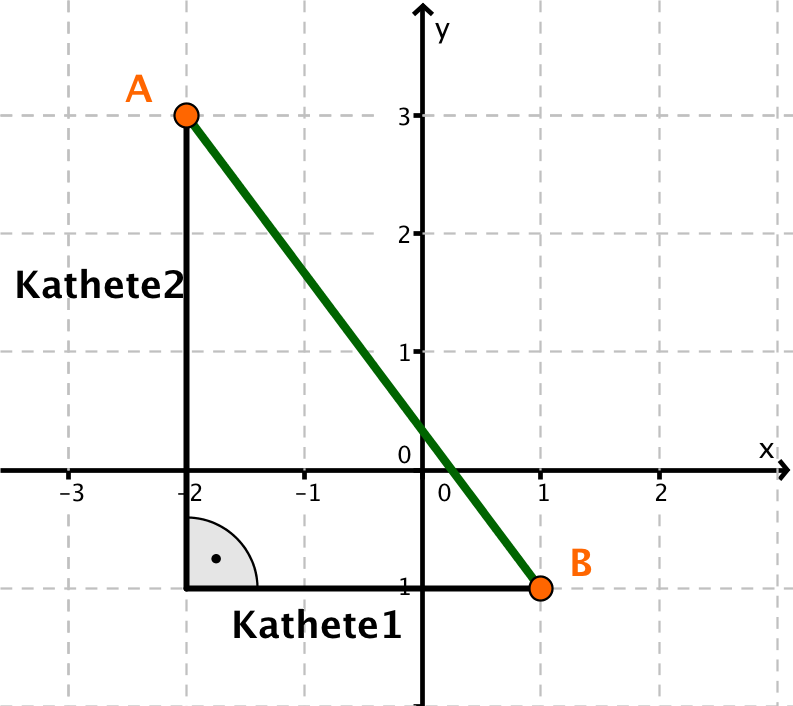
Wende den Satz des Pythagoras an. Die gesuchte Strecke ist die Hypotenuse.
Die Strecke [AB] hat die Länge 5.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
