Gemischte Aufgaben zu Abbildungen in der Ebene

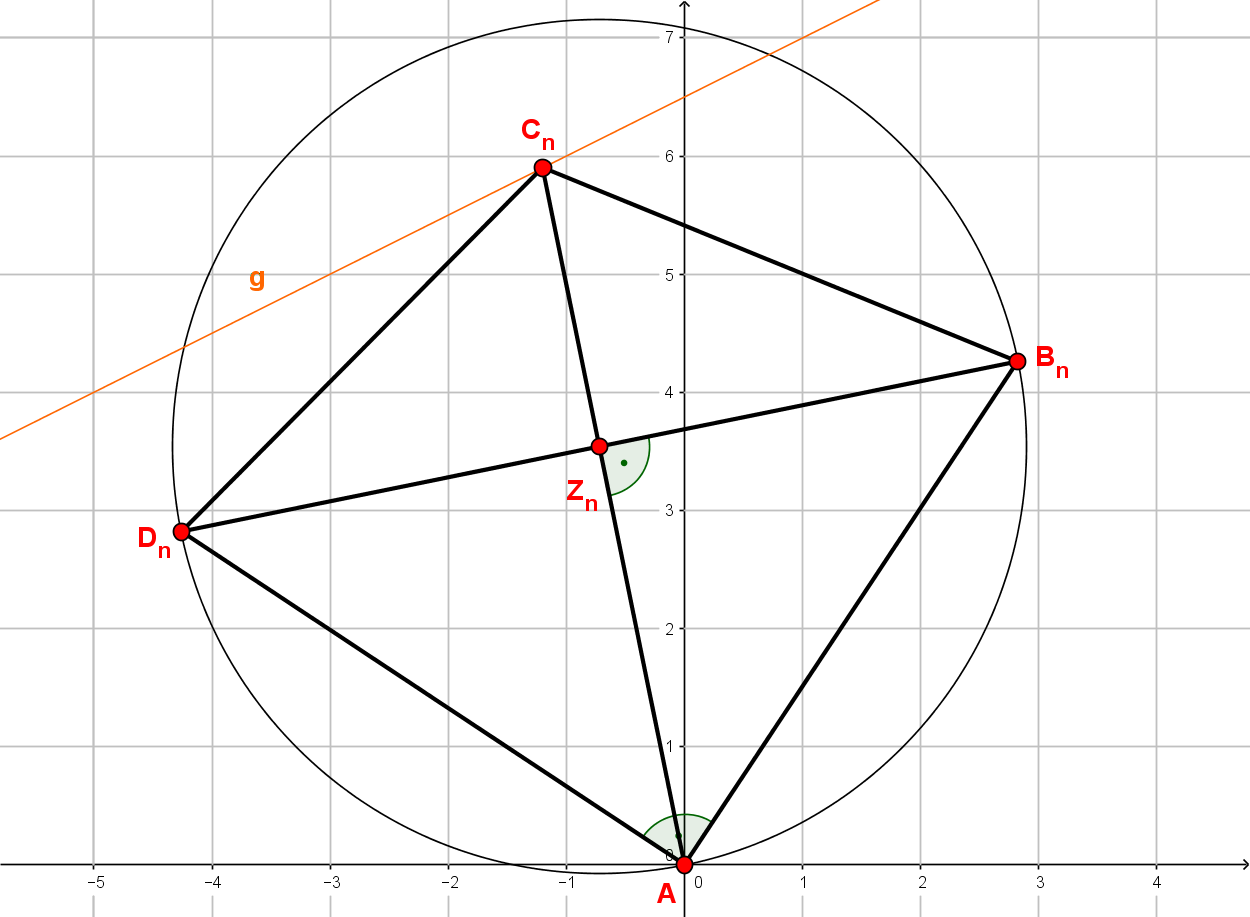
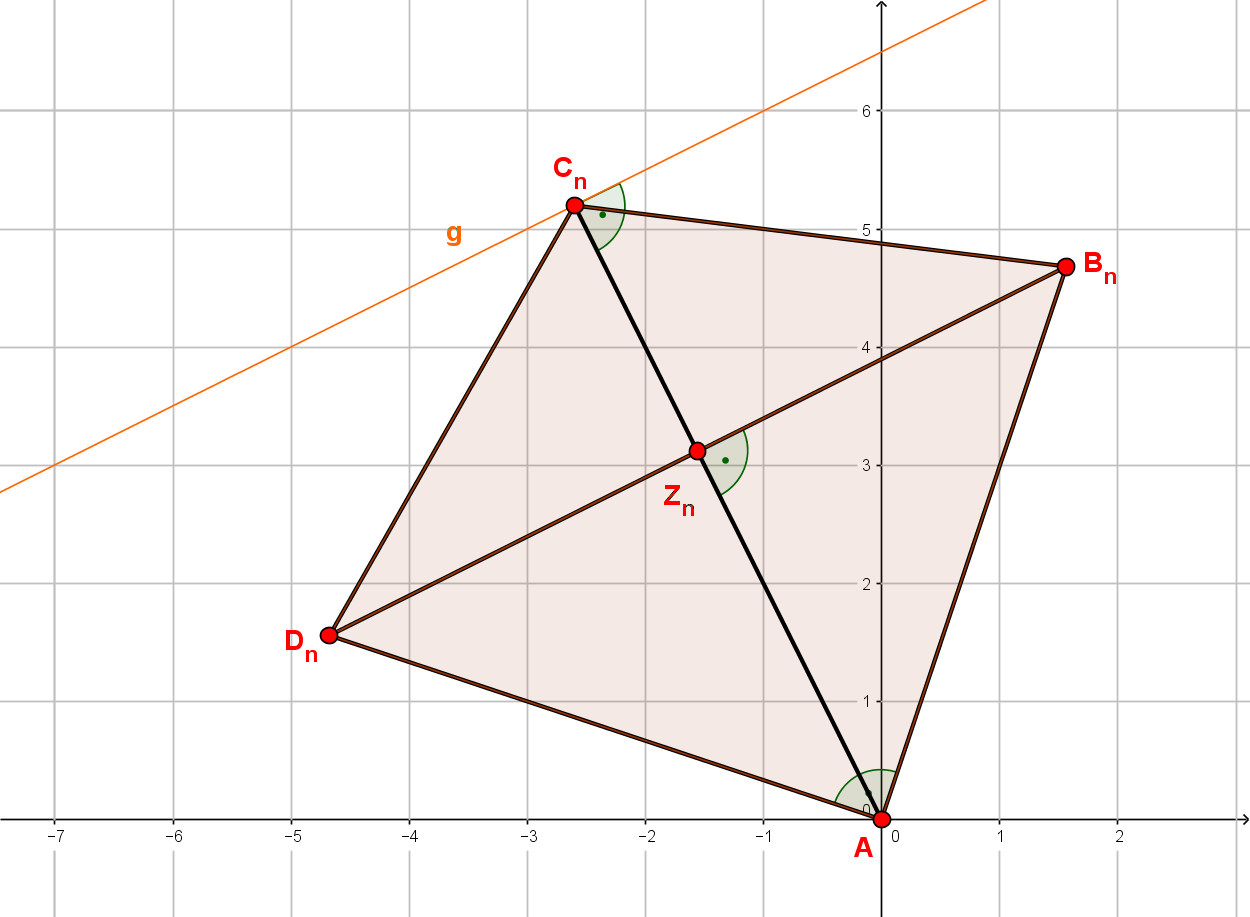
Die Eckpunkte $C_{n}$ der Drachenvierecke $A B_{n} C_{n} D_{n}$ liegen auf der Geraden g mit $y = 0,5 x + 6,5$ . Die Punkte $Z_{n}$ sind die Diagonalenschnittpunkte, die Geraden $A C_{n}$ sind die Symmetrieachsen der Drachenvierecke.

Es gilt: $A (0 | 0)$ ; $∢ D_{n} A B_{n} = 90^{\circ}; A Z_{n} : Z_{n} C_{n} = 3 : 2$

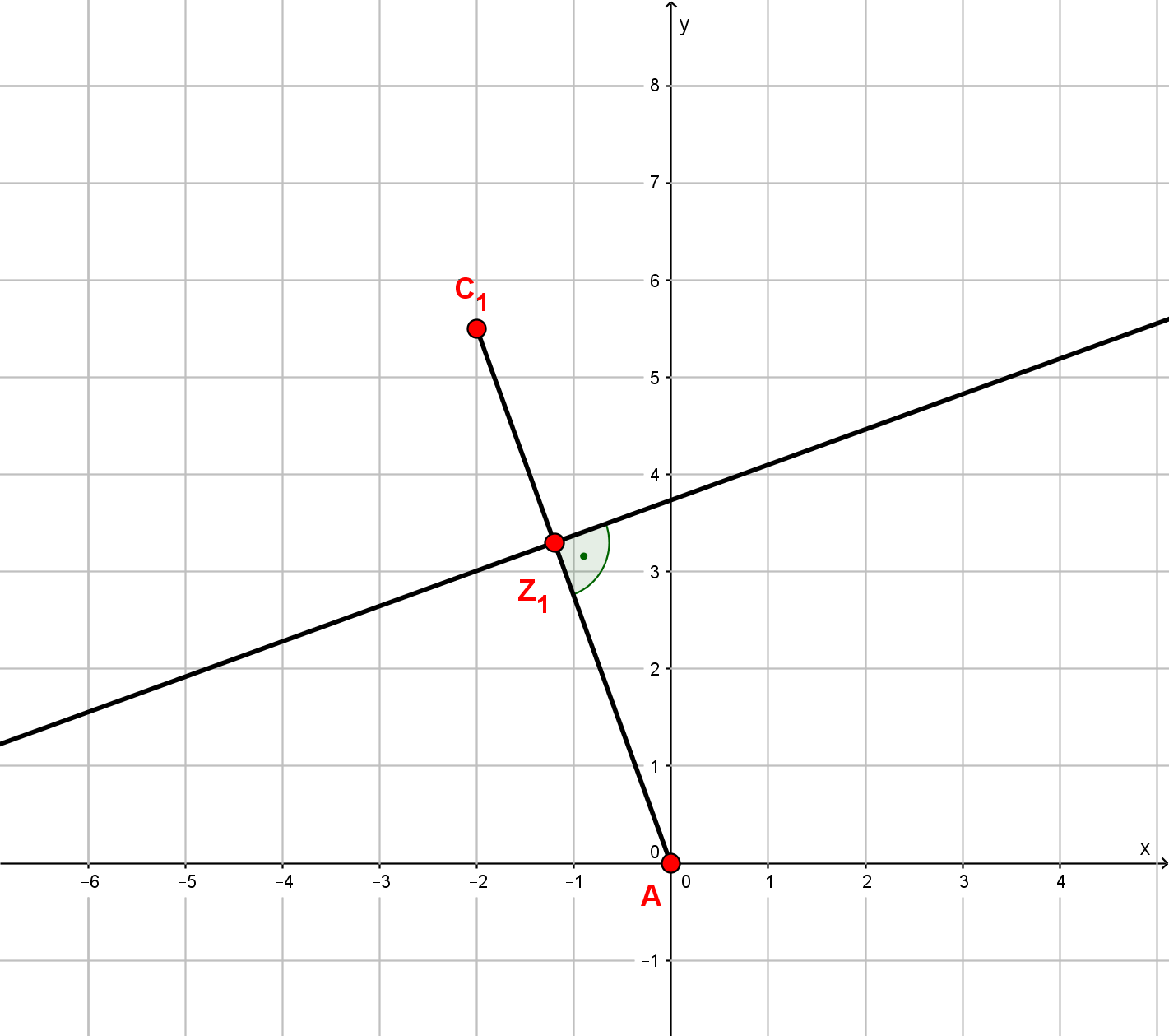
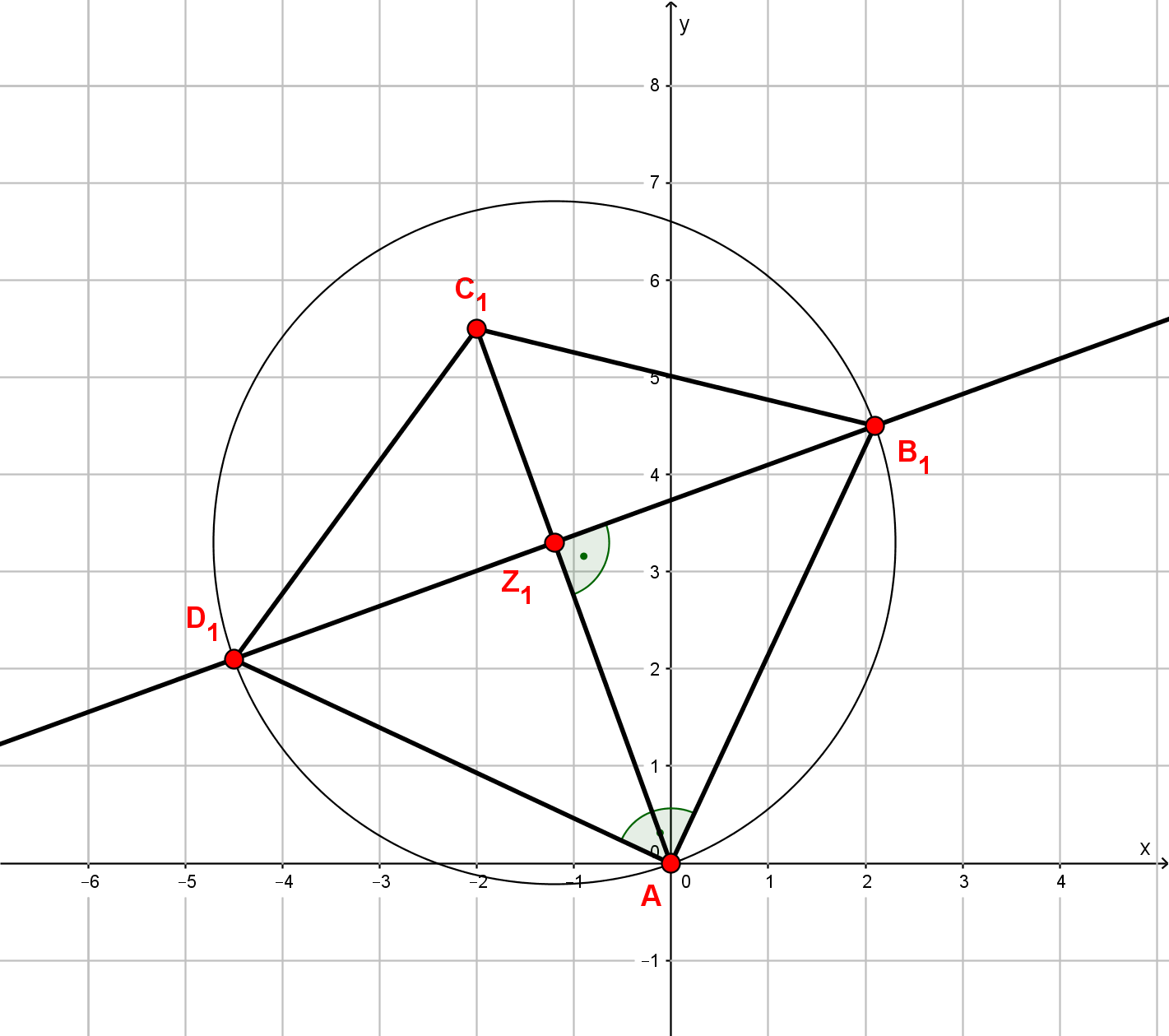
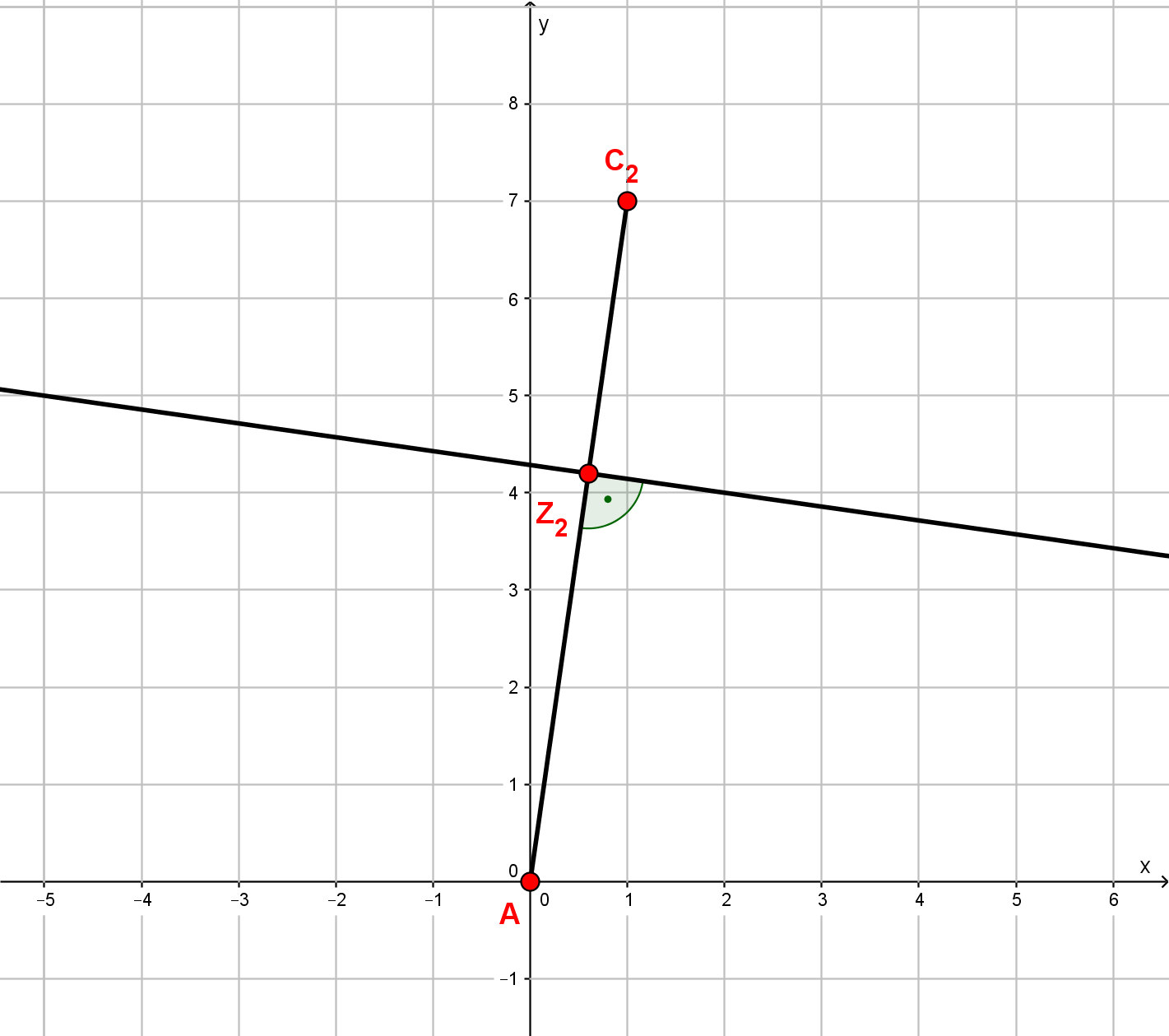
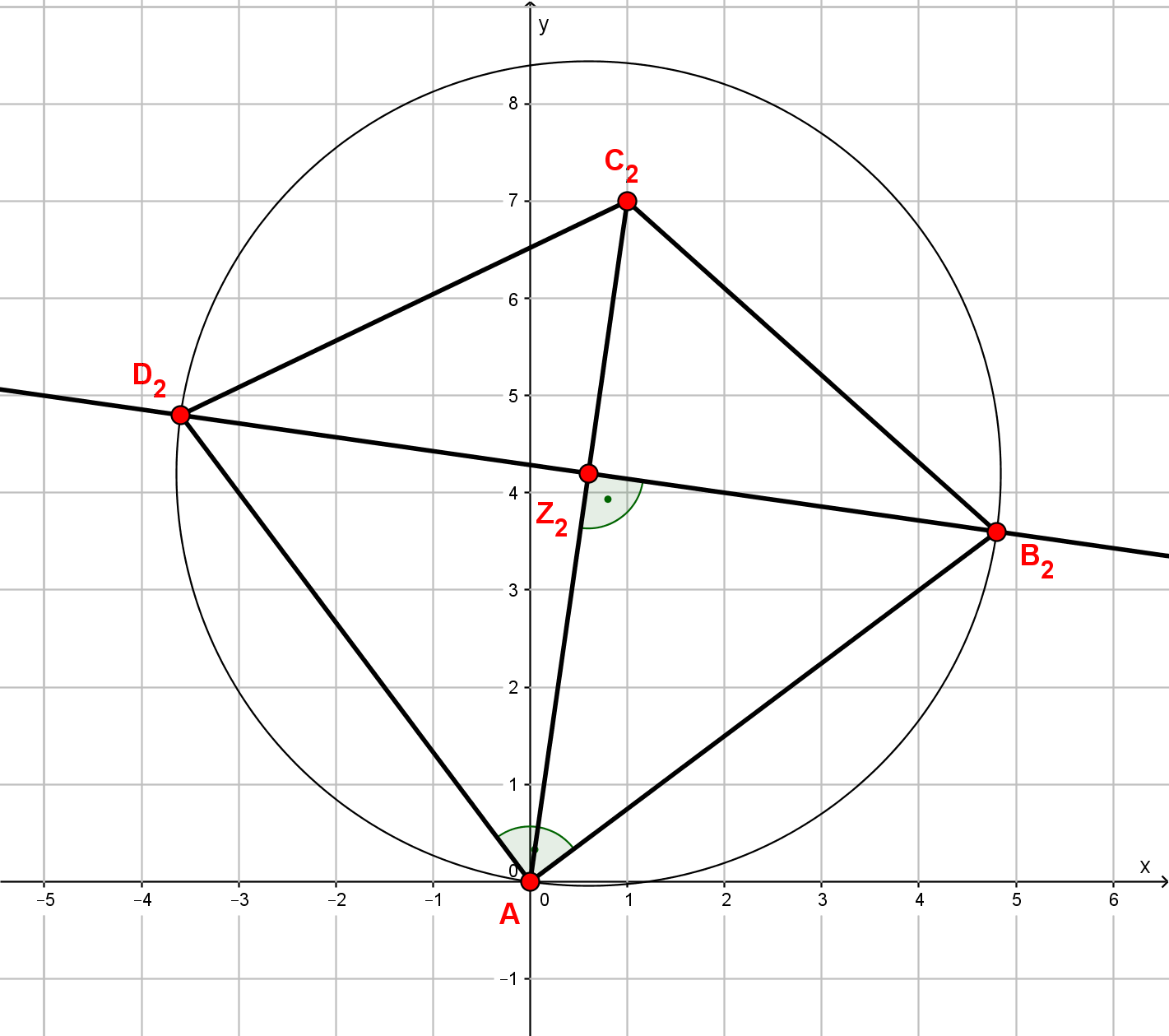
Zeichne die Drachenvierecke $A B_{1} C_{1} D_{1}$ und $A B_{2} C_{2} D_{2}$ für $x = - 2$ und $x = 1$ in ein Koordinatensystem! Für die Zeichnung:
$- 6 ≦ x ≦ 6; - 1 ≦ y ≦ 9$
$1 L E \hat{=} 1 c m$

Für das erste Drachenviereck:
Gegeben sind: $A (0 | 0)$ , $Z_{1} (x_{1} | 0,5 x_{1} + 6,5)$ , $A Z_{1} : Z_{1} C_{1} = 3 : 2$ , $∢ D_{1} A B_{1} = 90^{\circ}$ und $x_{1} = - 2$
Du zeichnest zuerst den Punkt $A$ in ein Koordinatensystem ein.
Dann berechnest du die Koordinaten von $C_{1}$ .
$C_{1} (- 2 | - 2 \cdot 0,5 + 6,5) = (- 2 | 5,5)$
Du trägst den Punkt $C_{1}$ in ein Koordinatensystem ein.
Dann berechnest die Koordinaten von $Z_{1}$ . Dafür multiplizierst du die Koordinaten von $C_{1}$ mit $\frac{3}{5}$ . Das kannst du aus dem Verhältnis $3 : 2$ rauslesen.
$Z_{1} = (- 2 \cdot \frac{3}{5} | 5,5 \cdot \frac{3}{5}) = (- 1,2 | 3,3)$
Diesen Punkt trägst du wieder ein.
Dann konstruierst du eine Senkrechte zu $[A C_{1}]$ , die durch den Punkt $Z_{1}$ geht. Auf dieser werden später $B_{1}$ und $D_{1}$ sein.
Du weißt, dass bei $A$ ein rechter Winkel vorliegt und, dass $Z_{1}$ Mittelpunkt von $B_{1}$ und $D_{1}$ ist. Du kannst also erkennen, dass du einen Thaleskreis benutzen kannst, um $B_{1}$ und $D_{1}$ zu finden. Die Schnittpunkte mit diesem sind die Punkte $B_{1}$ und $D_{1}$ .
Du zeichnest also einen Kreis mit Mittelpunkt $Z_{1}$ und Radius $Z_{1} A$ in deine Skizze.
Für das zweite Drachenviereck:
Gegeben sind: $A (0 | 0)$ , $Z_{2} (x_{2} | 0,5 x_{2} + 6,5)$ , $A Z_{2} : Z_{2} C_{2} = 3 : 2$ , $∢ D_{2} A B_{2} = 90^{\circ}$ und $x_{2} = 1$
Du zeichnest zuerst den Punkt $A$ in ein Koordinatensystem ein.
Dann berechnest du die Koordinaten von $C_{2}$ .
$C_{2} (1 | 1 \cdot 0,5 + 6,5) = (1 | 7)$
Du trägst den Punkt $C_{2}$ in ein Koordinatensystem ein.
Dann berechnest die Koordinaten von $Z_{2}$ . Dafür multiplizierst du die Koordinaten von $C_{2}$ mit $\frac{3}{5}$ . Das kannst du aus dem Verhältnis $3 : 2$ rauslesen.
$Z_{2} = (- 2 \cdot \frac{3}{5} | 5,5 \cdot \frac{3}{5}) = (- 1,2 | 3,3)$
Diesen Punkt trägst du wieder ein.
Dann konstruierst du eine Senkrechte zu $[A C_{2}]$ , die durch den Punkt $Z_{2}$ geht. Auf dieser werden später $B_{2}$ und $D_{2}$ sein.
Du weißt, dass bei $A$ ein rechter Winkel vorliegt und, dass $Z_{2}$ Mittelpunkt von $B_{2}$ und $D_{2}$ ist. Du kannst also erkennen, dass du einen Thaleskreis benutzen kannst, um $B_{2}$ und $D_{2}$ zu finden. Die Schnittpunkte mit diesem sind die Punkte $B_{2}$ und $D_{2}$ .
Du zeichnest also einen Kreis mit Mittelpunkt $Z_{2}$ und Radius $Z_{2} A$ in deine Skizze.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Koordinaten der Punkte $Z_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $C_{n}$ !

Gegeben sind die Koordinaten der Punkte $C_{n} (x | 0,5 x + 6,5)$ . Es gilt $0 Z_{n} : Z_{n} | C_{n} = 3 : 2$
Wenn zum Beispiel $C_{n}$ $5$ Längeneinheiten vom Ursprung entfernt ist, dann ist $Z_{n}$ $3$ Längeneinheiten vom Ursprung entfernt. Daraus folgt, dass $Z_{N}$ immer auf $\frac{3}{5}$ des Weges vom Ursprung zu $C_{n}$ liegt. Man multipliziert also die $x$ - und $y$ -Koordinaten von $Z_{n}$ mit $\frac{3}{5}$
$\Rightarrow Z_{n} (0,6 x | 0,6 \cdot (0,5 x + 6,5) = (0,6 x | 0,3 x + 3,9)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeige, dass gilt: $A Z_{n} : A B_{n} = 1 : \sqrt{2}$ !

Berechnung des Verältnisses $A Z_{N} : A B_{N}$
Gegeben: $Z_{n} (0,6 x | 0,3 + 3,9)$
$B_{n}$ liegt auf einer Senkrechten zu $[A Z_{n}]$ , die durch $Z_{n}$ führt.
Aus diesen Informationen kannst du entnehmen, dass $B_{n}$ , $Z_{n}$ und $O$ ein rechtwinkliges Dreieck $△ B_{n} Z_{n} A$ bilden. Durch den rechten Winkel $∢ D_{n} A B_{n}$ gibt es einen Thaleskreis mit Mittelpunkt $Z_{n}$ , der durch $D_{n}$ , $A$ und $B_{n}$ geht. Es gilt also $Z_{n} A = Z_{n} B_{n}$ .
$\begin{array}{lcr} {A Z_{n}}^{2} + {Z_{n} B_{n}}^{2} = {A B_{n}}^{2} \\ \Leftrightarrow & 2 {A Z_{n}}^{2} = {A B_{n}}^{2} \\ \Leftrightarrow & \sqrt{2} \cdot A Z_{n} = A B_{n} \end{array}$
$\Rightarrow A Z_{n} : A B_{n} = 1 : \sqrt{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Ermittle die Gleichung des Trägergraphen $t$ der Punkte $B_{n}$ !

Gegeben sind $Z_{N} (0,6 x | 0,3 x + 3,9)$ und $A (0 | 0)$ .
Wenn $A$ um $90^{\circ}$ um $Z_{n}$ gedreht wird, entsteht $B_{n}$ . Wir drehen $A$ also um einen beliebigen Punkt.
$\vec{O B_{n}} = (\begin{array}{cc} c o s (α) & - s i n (α) \\ s i n (α) & c o s (α) \end{array}) \cdot \vec{Z_{n} A} + \vec{O Z_{n}}$
$= (\begin{array}{cc} c o s (90^{\circ}) & - s i n (90^{\circ}) \\ s i n (90^{\circ}) & c o s (90^{\circ}) \end{array}) \cdot (\begin{array}{c} - 0,6 x \\ - 0,3 x - 3,9 \end{array}) + \vec{O Z_{n}}$
$= (\begin{array}{c} 0 \cdot - 0,6 x + - 1 \cdot (- 0,3 x + - 3,9) \\ 1 \cdot - 0,6 x + 0 \cdot (0,3 x + 3,9) \end{array}) + (\begin{array}{c} 0,6 x \\ 0,5 x + 6,5 \end{array})$
$= (\begin{array}{c} 0,3 x + 3,9 \\ - 0,6 x \end{array}) + (\begin{array}{c} 0,6 x \\ 0,3 x + 3,9 \end{array})$
$= (\begin{array}{c} 0,9 x + 3,9 \\ - 0,3 x + 3,9 \end{array})$
Um den Trägergraphen zu ermitteln, übernimmst du aus den Ortsvektoren $\vec{O B_{n}}$ folgende Informationen über die Koordinaten von $B_{n}$ :
$x_{B_{n}} = 0,9 x + 3,9$
$\Leftrightarrow \frac{10}{9} x_{B_{n}} - \frac{13}{3} = x$
$y_{B_{n}} = - 0,3 x + 3,9$
Jetzt musst du nur noch $x$ in die untere Gleichung einsetzen und du hast den Trägergraphen ermittelt.
$y_{B_{n}} = - 0,3 \cdot (\frac{10}{9} x - \frac{13}{3}) + 3,9$
$y_{B_{n}} = - \frac{1}{3} x_{B_{n}} + 5,2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Wert für $x$ , für den die Symmetrieachse $A C_{3}$ senkrecht zur Geraden $g$ steht!

Gegeben: $g : y = 0,5 x + 6,5$ und $\vec{A C_{N}} = (\begin{array}{c} x \\ 0,5 x + 6,5 \end{array})$
Der Richtungsvektor der Geraden $g$ muss orthogonal zu $\vec{A C_{n}}$ sein:
$\vec{g} \circ \vec{A C_{N}} = 0$
$\Rightarrow (\begin{array}{c} 1 \\ 0,5 \end{array}) \circ (\begin{array}{c} x \\ 0,5 x + 6,5 \end{array}) = 0$
$\Leftrightarrow x + 0,25 x + 3,25 = 0$
$\Leftrightarrow 1,25 x + 3,25 = 0$
$\Leftrightarrow x = - 2,6$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
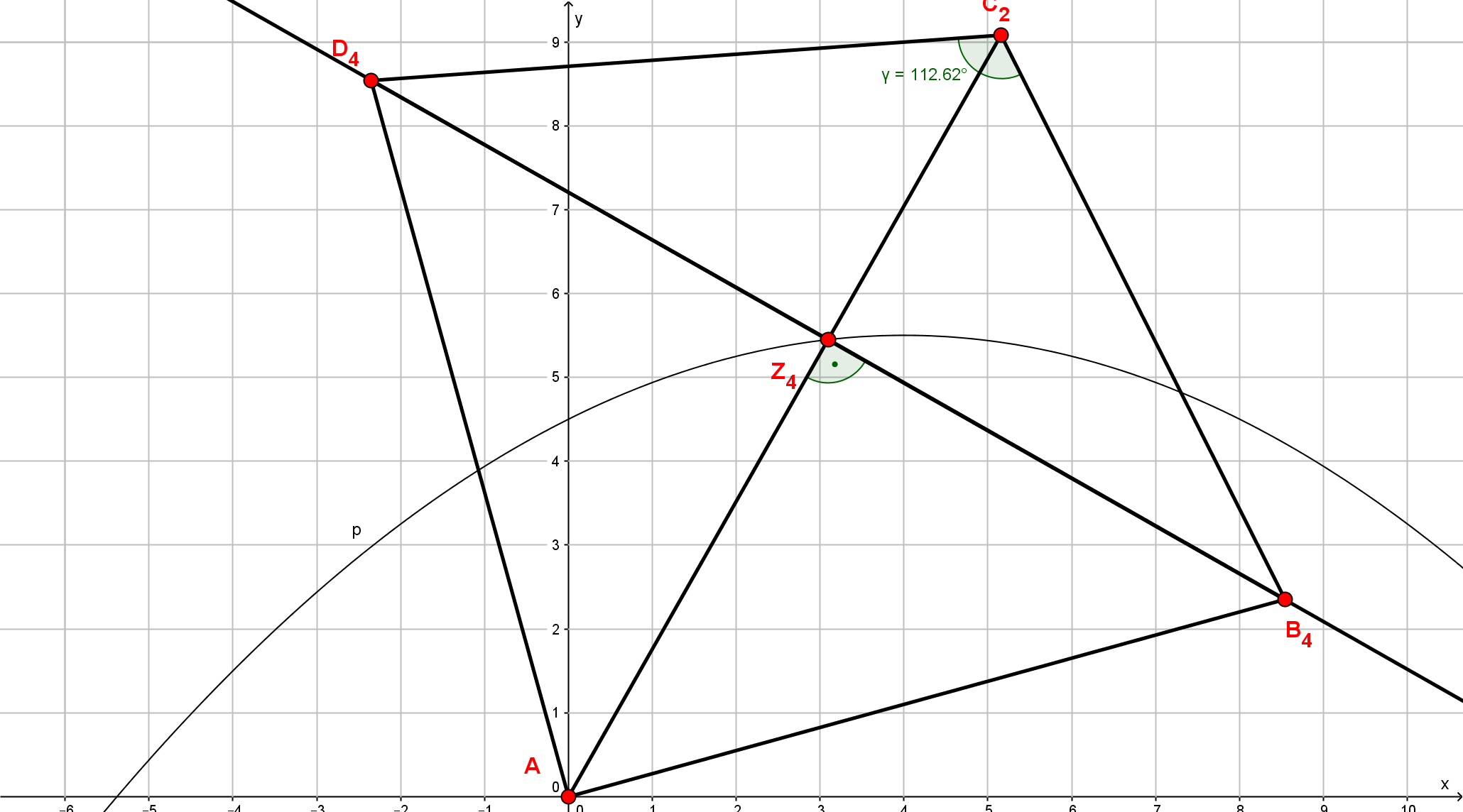
Unter den Drachenvierecken $A B_{n} C_{n} D_{n}$ besitzt das Drachenviereck $A B_{0} C_{0} D_{0}$ einen extremen Flächeninhalt. Berechnen sie dazu die $x$ -Koordinate des Punktes $B_{0}$ !

Gegeben sind $\vec{A B_{n}} = (\begin{array}{c} 0,9 x + 3,9 \\ - 0,3 x + 3,9 \end{array})$ und $\vec{A C_{n}} = (\begin{array}{c} x \\ 0,5 x + 6,5 \end{array})$ .
Das Drachenviereck besteht aus zwei gleichgroßen Dreiecken, dessen Flächeninhalt du mit der Determinante ausrechnen kannst.
$\begin{array}{lcr} A (x) & = 2 \cdot \frac{1}{2} \cdot | \begin{array}{cc} \vec{A B_{n}} & \vec{A C_{n}} \end{array} | \\ = | \begin{array}{cc} 0,9 x + 3,9 & x \\ - 0,3 x + 3,9 & 0,5 x + 6,5 \end{array} | \\ = (0,9 x + 3,9) \cdot (0,5 x + 6,5) - (- 0,3 x + 3,9) \cdot x \\ = 0,45 x^{2} + 7,8 x + 25,35 + 0,3 x^{2} - 3,9 x \\ = 0,75 x^{2} + 3,9 x + 25,35 \end{array}$
Du kennst jetzt den Flächeninhalt in Abhängigkeit von $x$ . Mit der quadratischen Ergänzung kannst du die Scheitelpunktform der Parabel ausrechnen und damit den Scheitelpunkt bestimmen.
$\begin{array}{lcr} A (x) & = 0,75 \cdot (x^{2} + 5,2 x + 33,8) \\ = 0,75 \cdot (x^{2} + 5,2 x + 33,8 + {2,6}^{2} - {2,6}^{2}) \\ = 0,75 (x + 2,6)^{2} + 27,04 \end{array}$
Aus der Scheitelpunktform liest du heraus, dass der Scheitelpunkt bei $S (- 2,6 | 27,04)$ liegt. Als letztes berechnest du die $x$ -Koordinate von $B_{0}$ .
$\begin{array}{lcr} x_{B_{n}} & = 0,9 x + 3,9 \\ = 0,9 \cdot - 2,6 + 3,9 \\ = 1,56 \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Punkt $Z_{4}$ liegt auf der Parabel $p$ mit $y = - \frac{1}{16} x^{2} + \frac{1}{2} x + 4,5$ .
Berechne die Koordinaten des Punktes $C_{4}$ und das Maß des Winkels $∢ D_{4} C_{4} B_{4}$ !

Gegeben sind:
$Z_{4} \in p : y = - \frac{1}{16} x^{2} + \frac{1}{2} x + 4,5$
$Z_{n} (0,6 x | 0,3 x + 3,9)$
Du kennst die Koordinaten aller Punkte $Z_{n}$ in allgemeiner Form. Außerdem weißt du, dass der Punkt $Z_{4}$ im Speziellen auf $p$ liegt, d. h. seine Koordinaten müssen die Parabelgleichung erfüllen. Du setzt also die Koordinaten von $Z_{n}$ in die Gleichung von $p$ ein und berechnest so den entsprechenden Wert für $x$ .
$0,3 x + 3,9 = - \frac{1}{16} (0,6 x)^{2} + \frac{1}{2} \cdot 0,6 x + 4,5$
$0 = - \frac{9}{400} x^{2} + 0,6$
$\Leftrightarrow x = \pm \frac{4 \sqrt{15}}{3}$
$Z_{4} (\frac{2 \sqrt{15}}{3} | 0,3 \cdot \frac{4 \sqrt{15}}{3} + 3,9 = \frac{39 + 4 \sqrt{15}}{10})$
$C_{4} (\frac{4 \sqrt{15}}{3} | 0,5 \cdot \frac{4 \sqrt{15}}{3} + 6,5 = \frac{39 + 4 \sqrt{15}}{6})$
Als letztes berechnest du den Winkel $∢ D_{4} C_{4} B_{4}$ mit den Vektoren $\vec{C_{4} B_{4}}$ und $\vec{C_{4} A}$ . Diesen musst du dann mit $2$ multiplizieren.
$\vec{O B_{n}} = (\begin{array}{c} 0,9 x + 3,9 \\ - 0,3 x + 3,9 \end{array})$ , $x = \frac{4 \sqrt{15}}{3}$
$\begin{array}{lcr} \vec{C_{4} B_{4}} & = (\begin{array}{c} \frac{2 \sqrt{15}}{3} - (0,9 \cdot \frac{4 \sqrt{15}}{3} + 3,9) \\ \frac{4 \sqrt{15}}{3} - (- 0,3 \cdot \frac{4 \sqrt{15}}{3} + 3,9) \end{array}) \\ = (\begin{array}{c} - \frac{117 + 16 \sqrt{15}}{30} \\ \frac{- 117 + 52 \sqrt{15}}{30} \end{array}) \end{array}$
$\vec{C_{4} A} = (\begin{array}{c} - \frac{4 \sqrt{15}}{3} \\ - \frac{39 + 4 \sqrt{15}}{6} \end{array})$
$\begin{array}{l} ∢ D_{4} C_{4} B_{4} = 2 α = 2 \cdot c o s^{- 1} (\frac{| - \frac{117 + 16 \sqrt{15}}{30} \cdot - \frac{4 \sqrt{15}}{3} + \frac{- 117 + 52 \sqrt{15}}{30} \cdot - \frac{39 + 4 \sqrt{15}}{6} |}{\sqrt{(- \frac{117 + 16 \sqrt{15}}{30})^{2} + (\frac{- 117 + 52 \sqrt{15}}{30})^{2}} \cdot \sqrt{(- \frac{4 \sqrt{15}}{3})^{2} + (- \frac{39 + 4 \sqrt{15}}{6})^{2}}}) \\ \approx {112,62}^{\circ} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇