Gemischte Aufgaben zu Abbildungen in der Ebene
Hier findest du Übungsaufgaben zu Abbildungen in der Ebene. Lerne, Objekte in der Ebene zu konstruieren und mit Matrizen abzubilden.
- 1
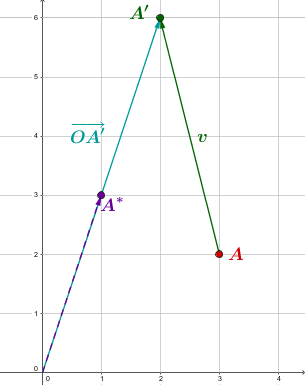
Verschiebe den Punkt um den Vektor zu und strecke anschließend den Ortsvektor um den Faktor . Gib die Koordinaten des Punktes an, der sich bei dieser Streckung ergibt.
- 2
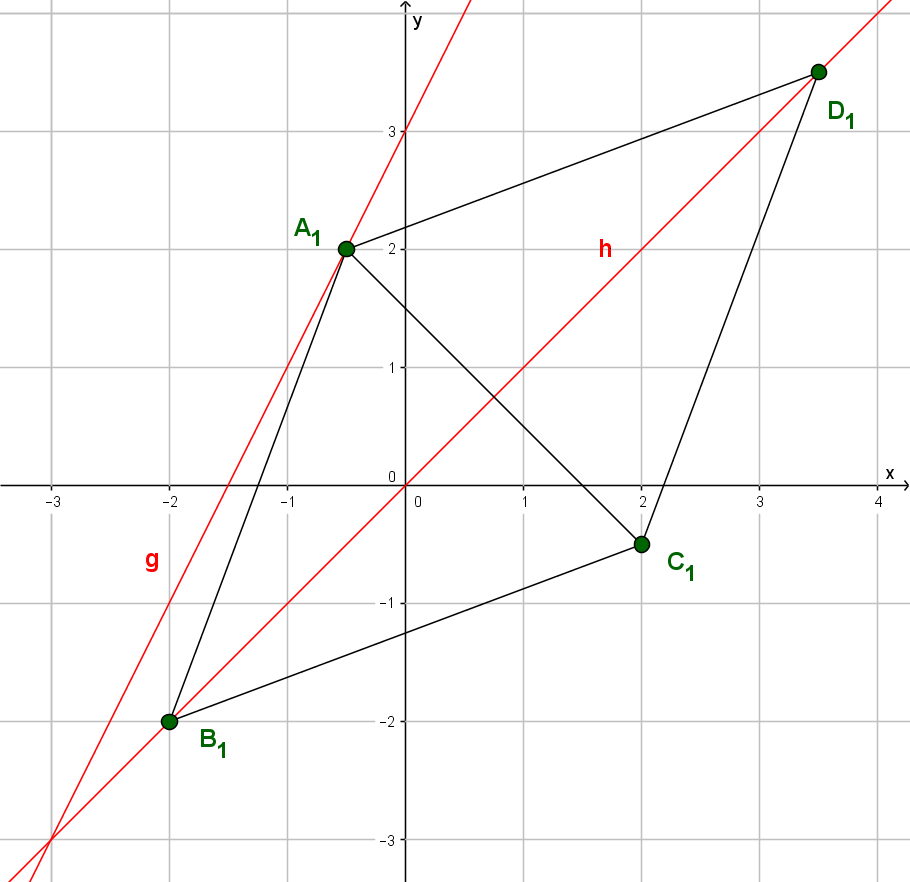
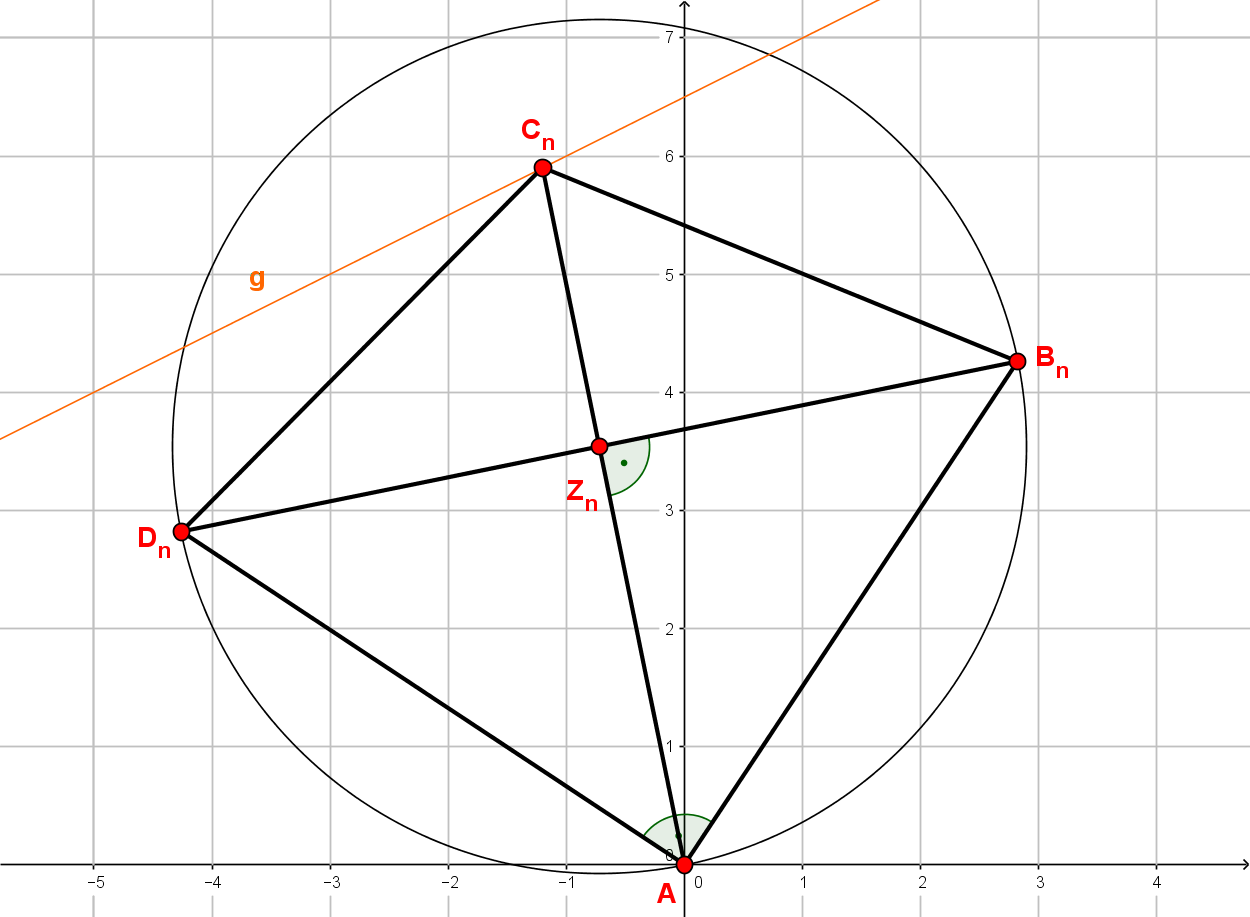
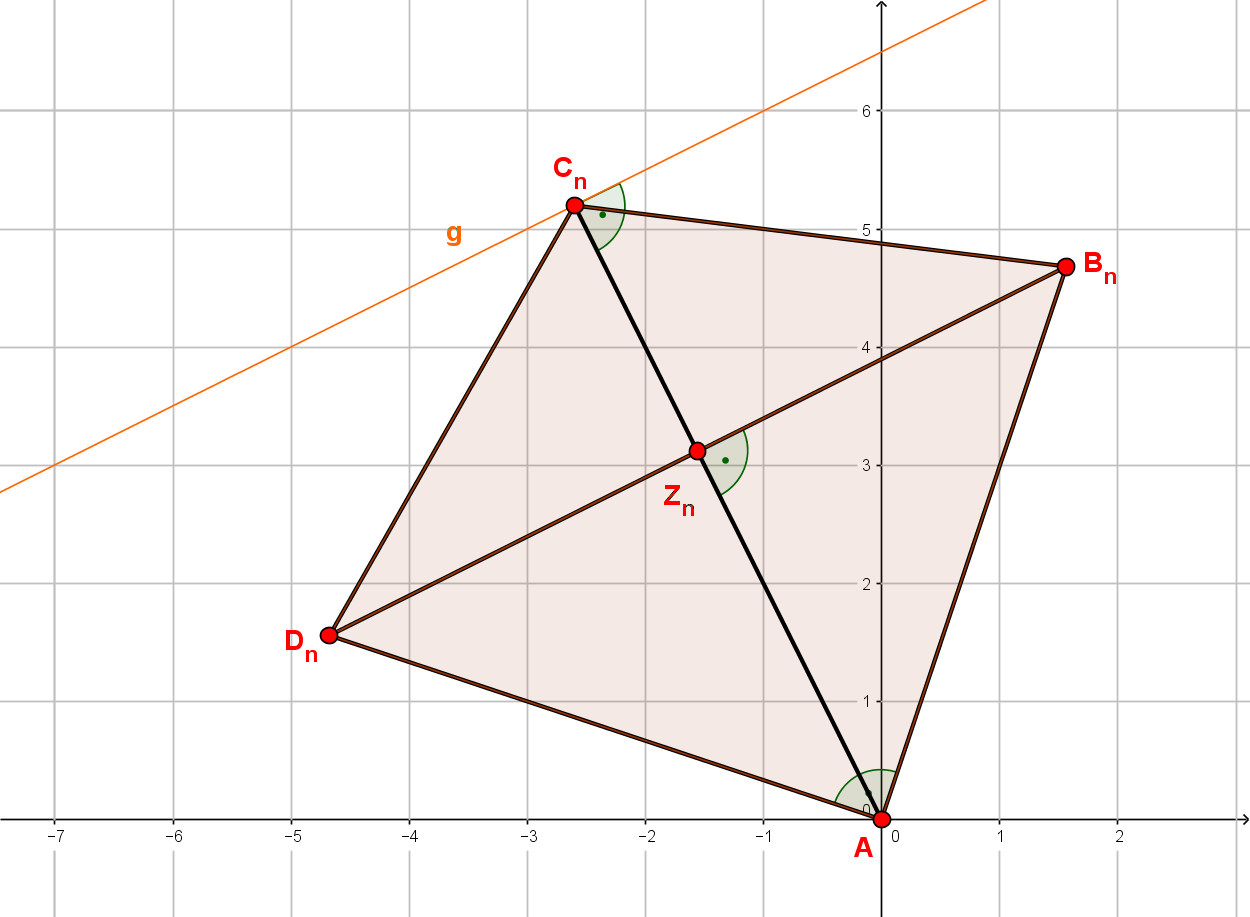
Die Gerade mit der Gleichung ist Symmetrieachse von Rauten . Die Diagonalen der Rauten liegen auf der Geraden . Die Punkte liegen auf der Geraden mit der Gleichung . Die Abszisse der Punkte ist stets um vier größer als die Abszisse der Punkte . Dabei gilt: -.
Runde im folgenden auf zwei Nachkommastellen!
Zeichne die Geraden und sowie die Raute für und die Raute für in ein Koordinatensystem! Für die Zeichnung: Längeneinheit ; .
Zeige, dass für die Punkte in Abhängigkeit von der Abszisse der Punkte gilt: ! Bestätige sodann durch Rechnung die untere Intervallgrenze der Rauten !
Begründe, warum sich für die obere Intervallgrenze ergibt und bestätige diese durch Rechnung!
Bestimme rechnerisch die Koordinaten der Punkte in Abhängigkeit von der Abszisse der Punkte !
Berechne den Flächeninhalt der Rauten in Abhängigkeit von der Abszisse der Punkte !
Die Seite der Raute verläuft senkrecht zur -Achse. Berechne die Koordinaten des Punktes !
In der Raute hat die Diagonale die gleiche Länge wie die Seite . Begründe, dass für die Diagonale gilt: !
- 3
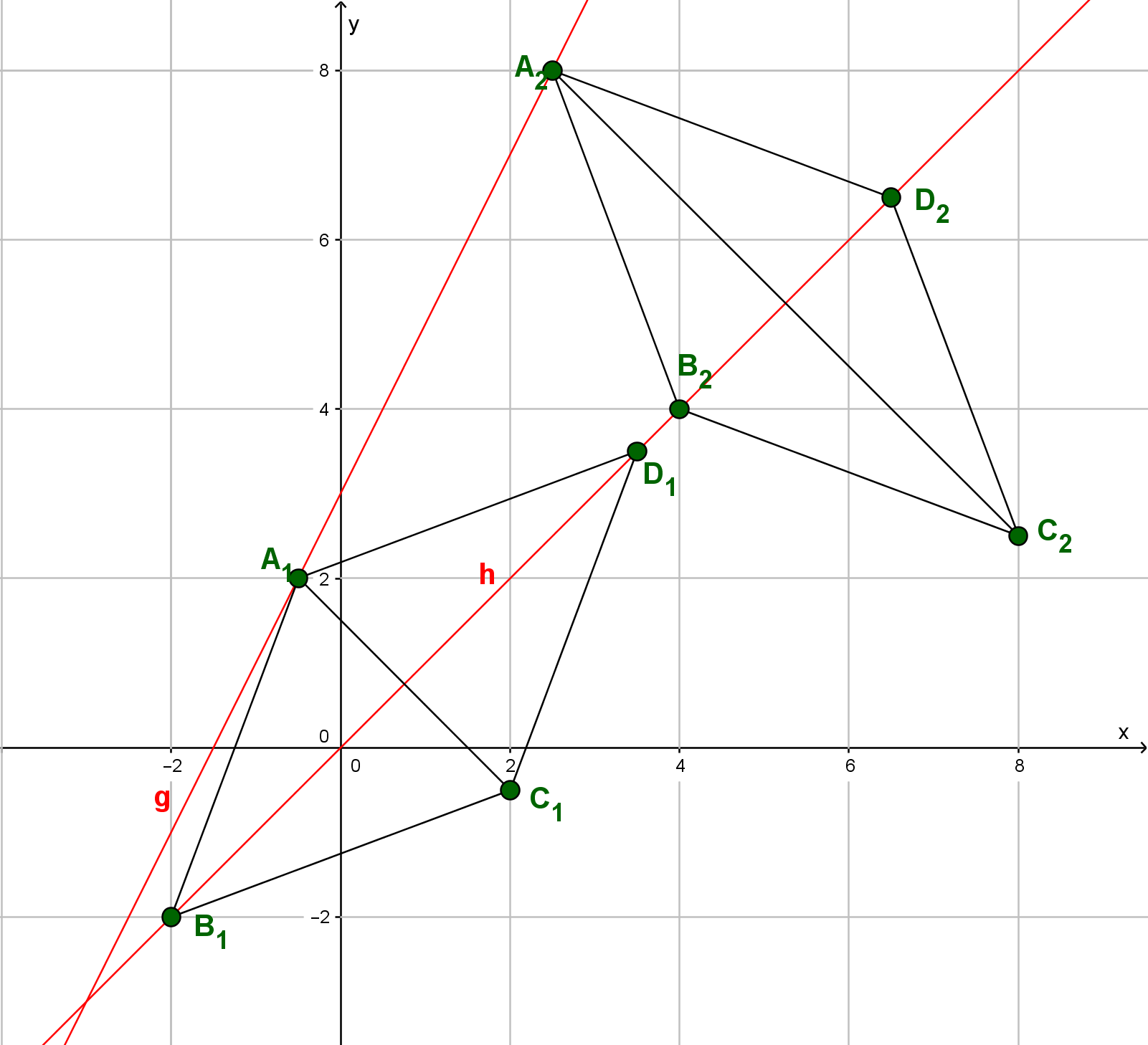
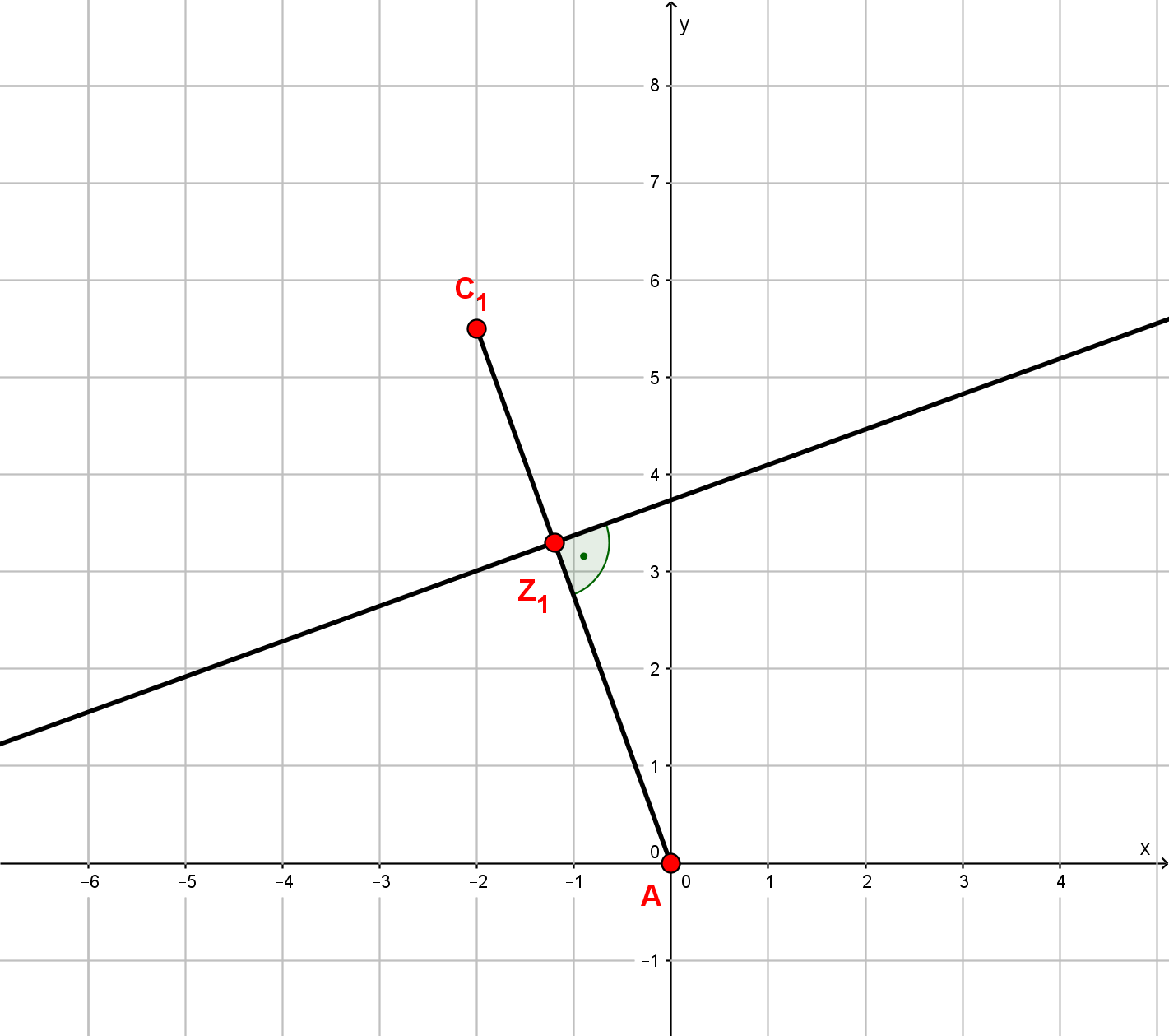
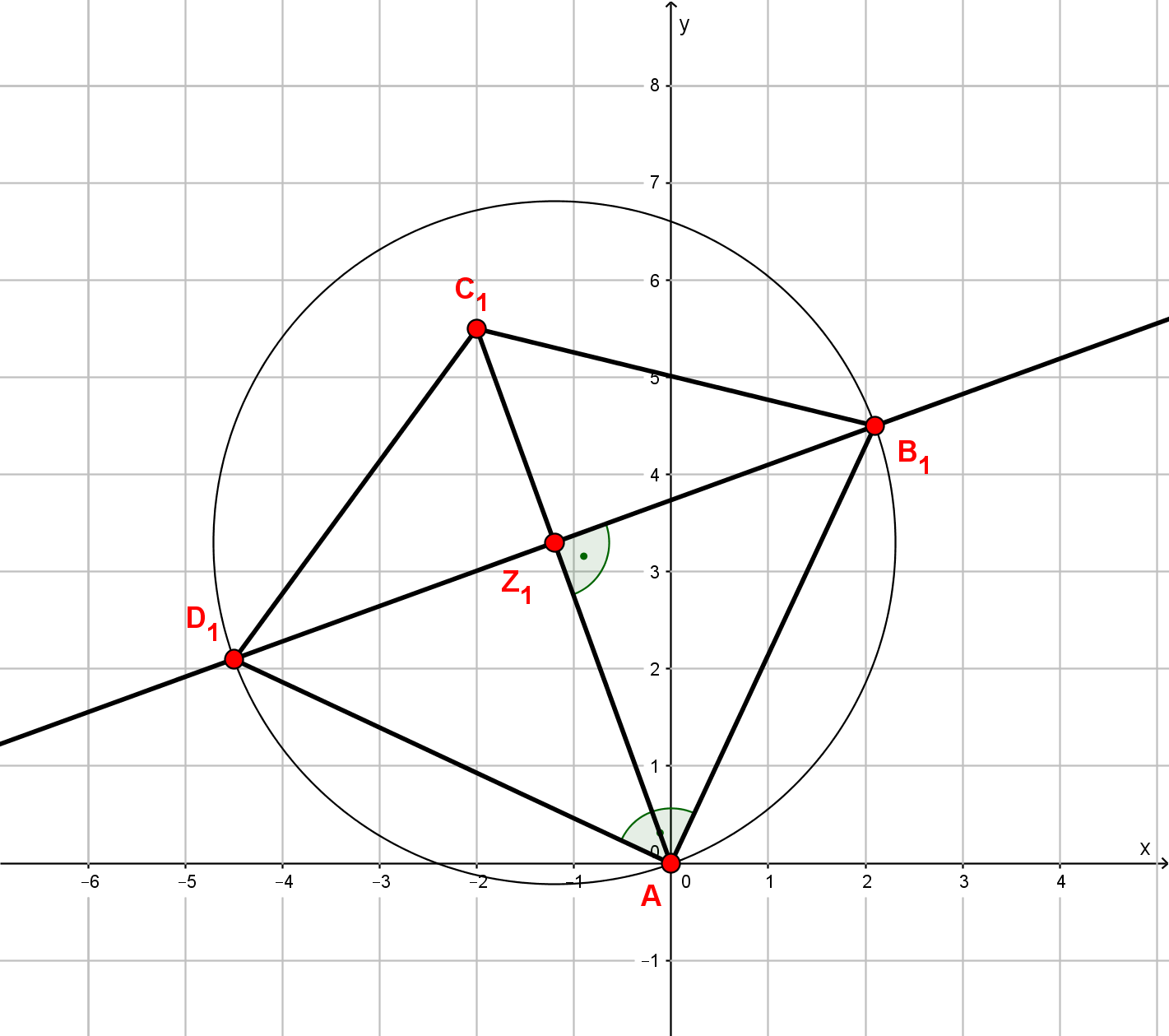
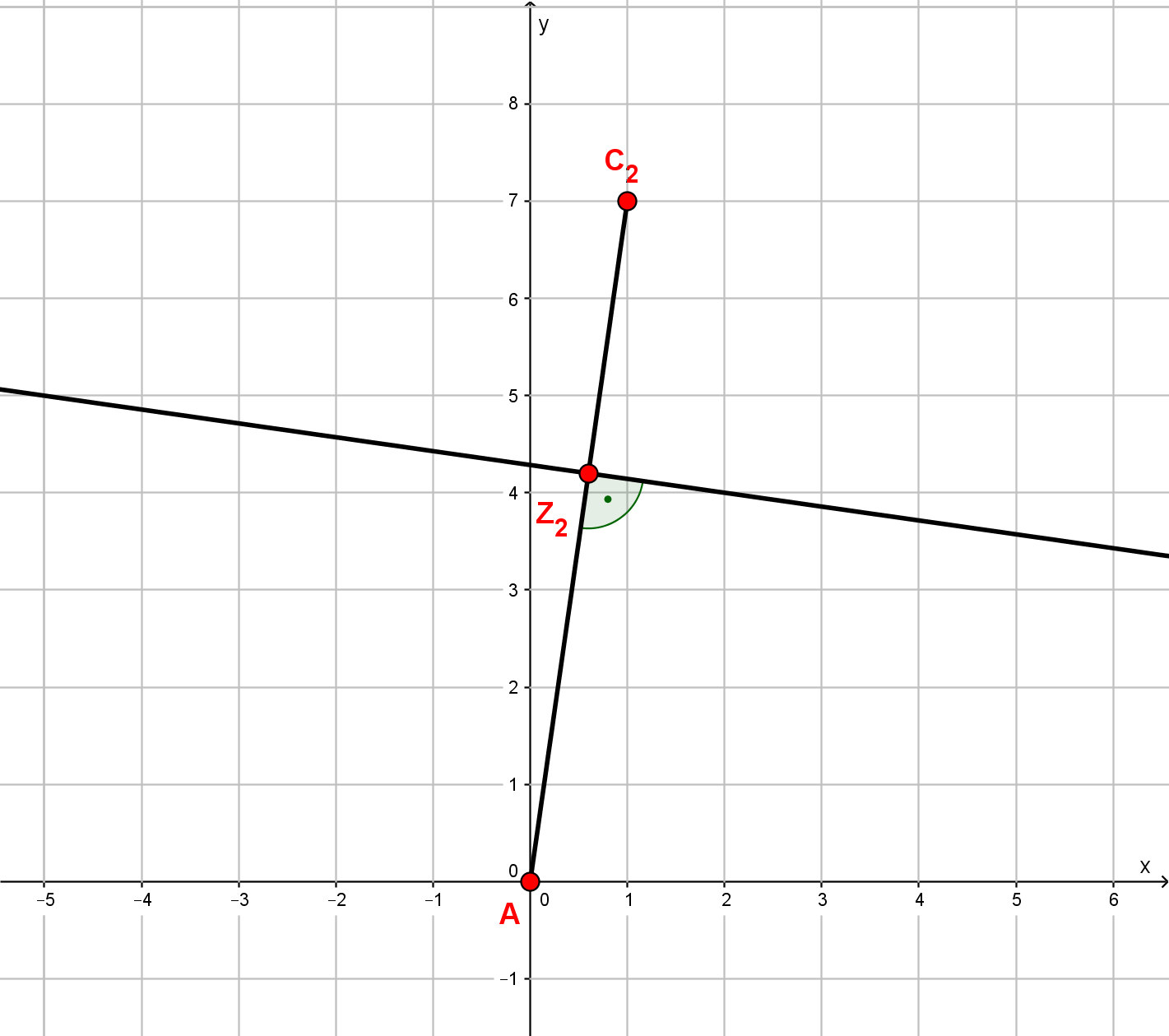
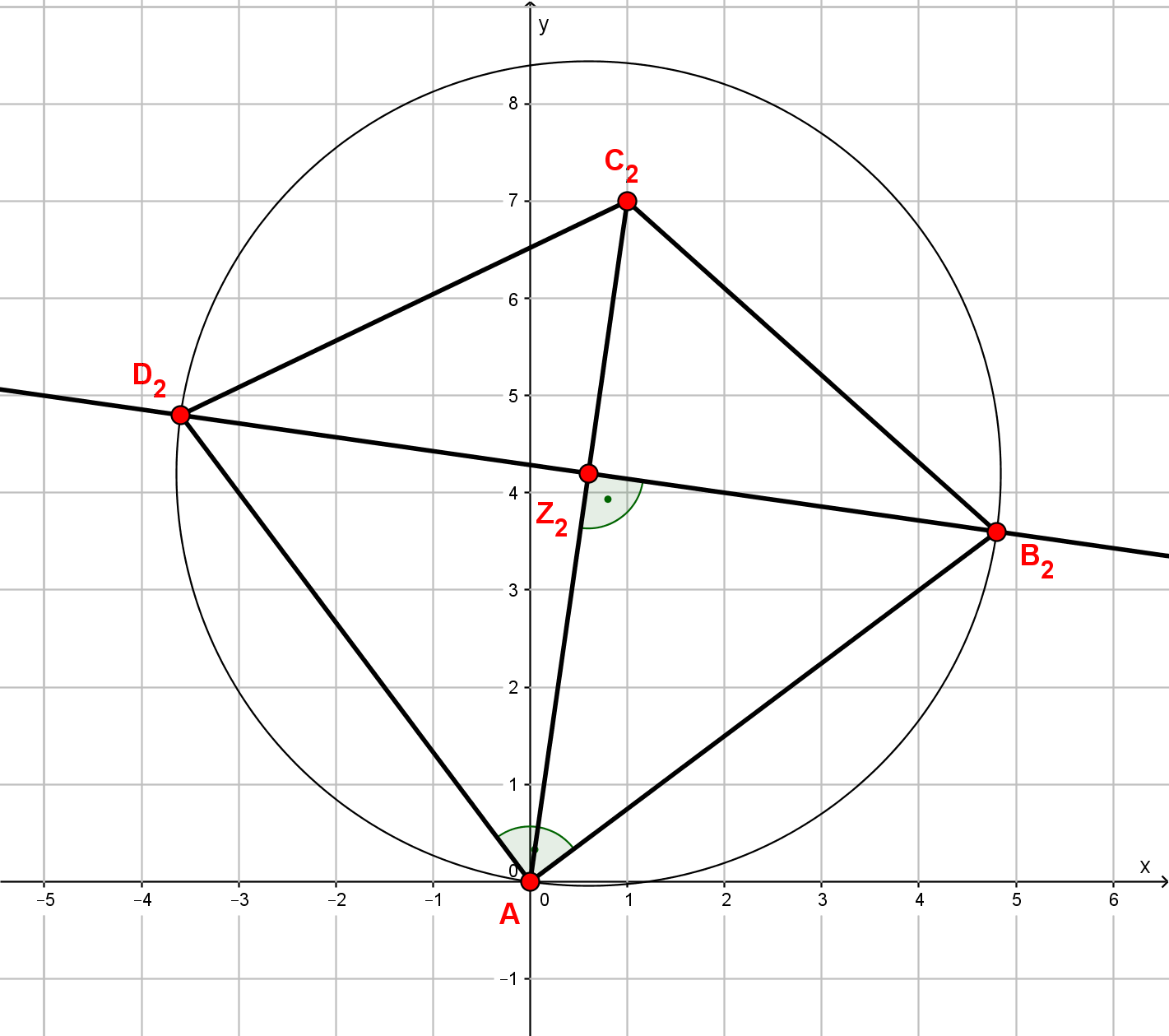
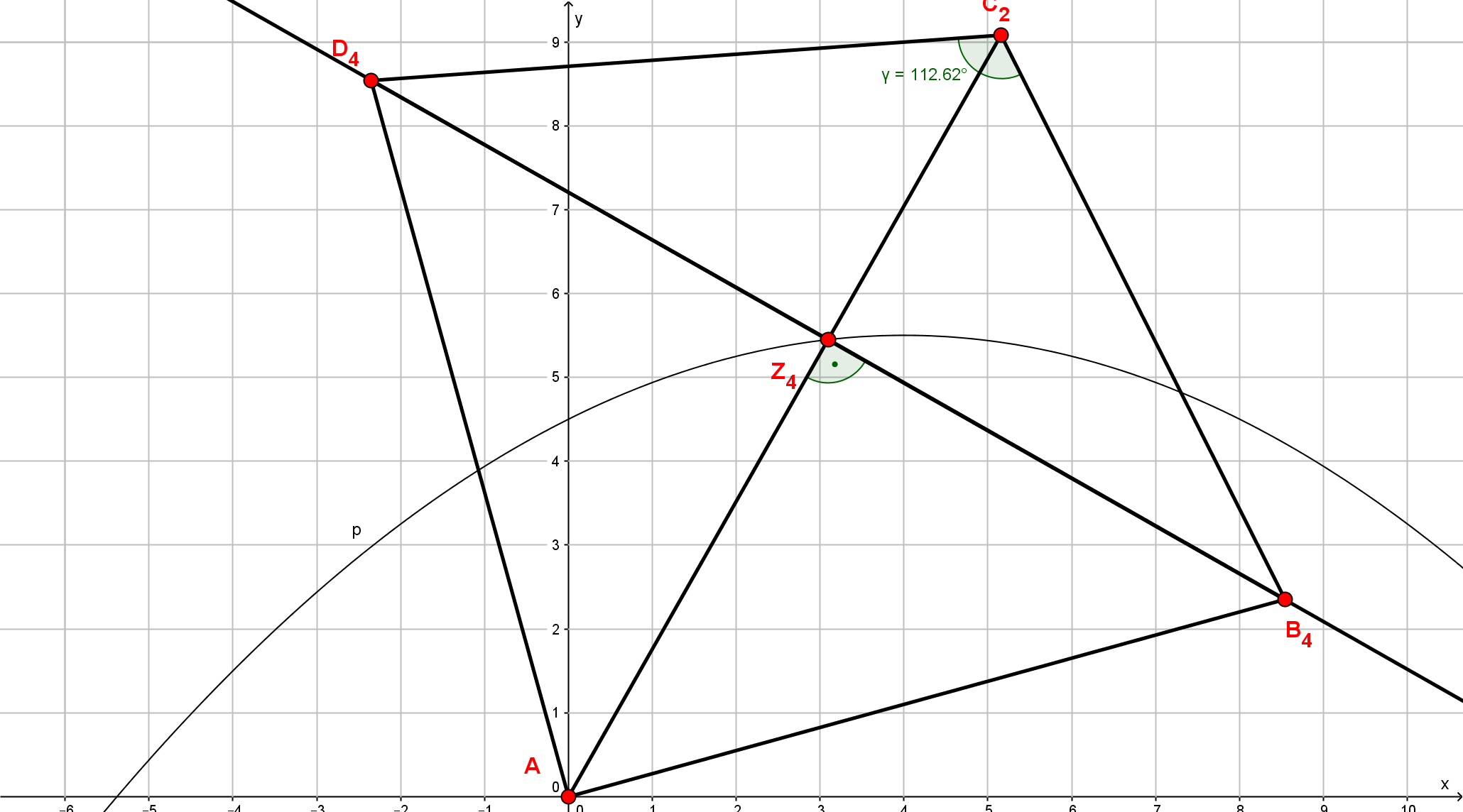
Die Eckpunkte der Drachenvierecke liegen auf der Geraden g mit . Die Punkte sind die Diagonalenschnittpunkte, die Geraden sind die Symmetrieachsen der Drachenvierecke.
Es gilt: ;
Zeichne die Drachenvierecke und für und in ein Koordinatensystem! Für die Zeichnung:
Berechne die Koordinaten der Punkte in Abhängigkeit von der Abszisse der Punkte !
Zeige, dass gilt: !
Ermittle die Gleichung des Trägergraphen der Punkte !
Berechne den Wert für , für den die Symmetrieachse senkrecht zur Geraden steht!
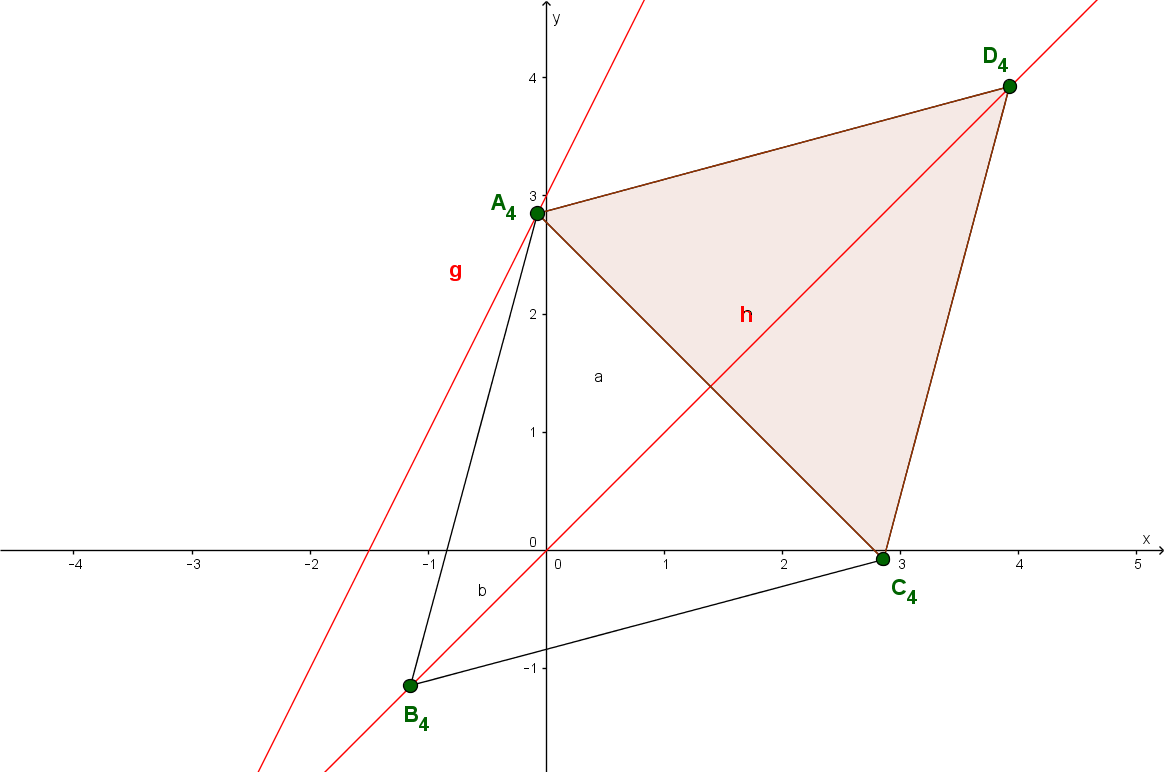
Unter den Drachenvierecken besitzt das Drachenviereck einen extremen Flächeninhalt. Berechnen sie dazu die -Koordinate des Punktes !
Der Punkt liegt auf der Parabel mit .
Berechne die Koordinaten des Punktes und das Maß des Winkels !
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?