Wie du vielleicht erkennen kannst, gibt es doch ein paar Regeln, nach denen man das Verhalten des Graphen einer Polynomfunktion vorhersagen kann.
Dazu betrachten wir abschließend alle drei Forschungsbeispiele und versuchen dabei herauszufinden, wie der Verlauf der Polynomfunktion von seinen Bestandteilen (und ) abhängt.
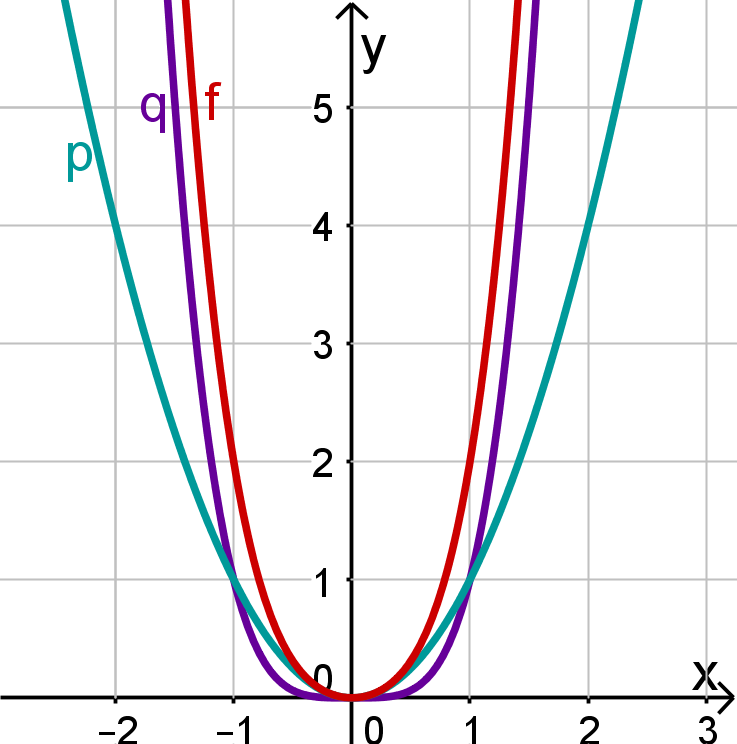
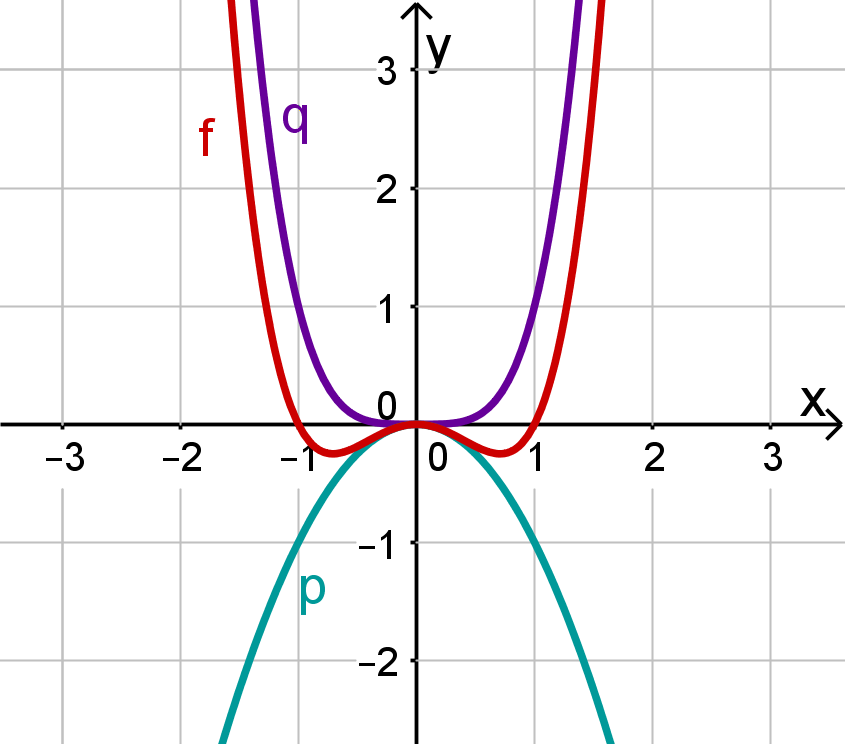
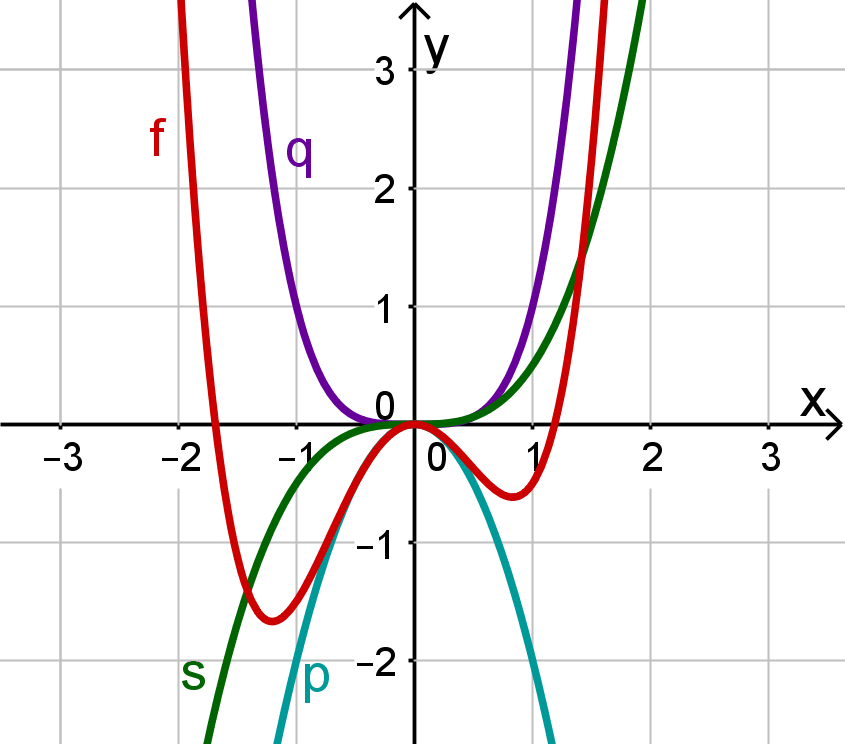
In allen drei Fällen nähert sich der Graph dem Graphen von für betragsmäßig große (also sehr große und sehr kleine) -Werte. Bei unseren Forschungsbeispielen war die Potenz mit dem höchsten Exponenten.
Allgemein gilt:
Für betragsmäßig große -Werte (also im Unendlichen) wird das Verhalten einer Polynomfunktion durch den Summanden mit dem höchsten vorkommenden Exponenten bestimmt.
Wie bei Potenzfunktionen gibt es nur vier Möglichkeiten für den charakteristischen Verlauf des Graphen einer ganzrationalen Funktion.
