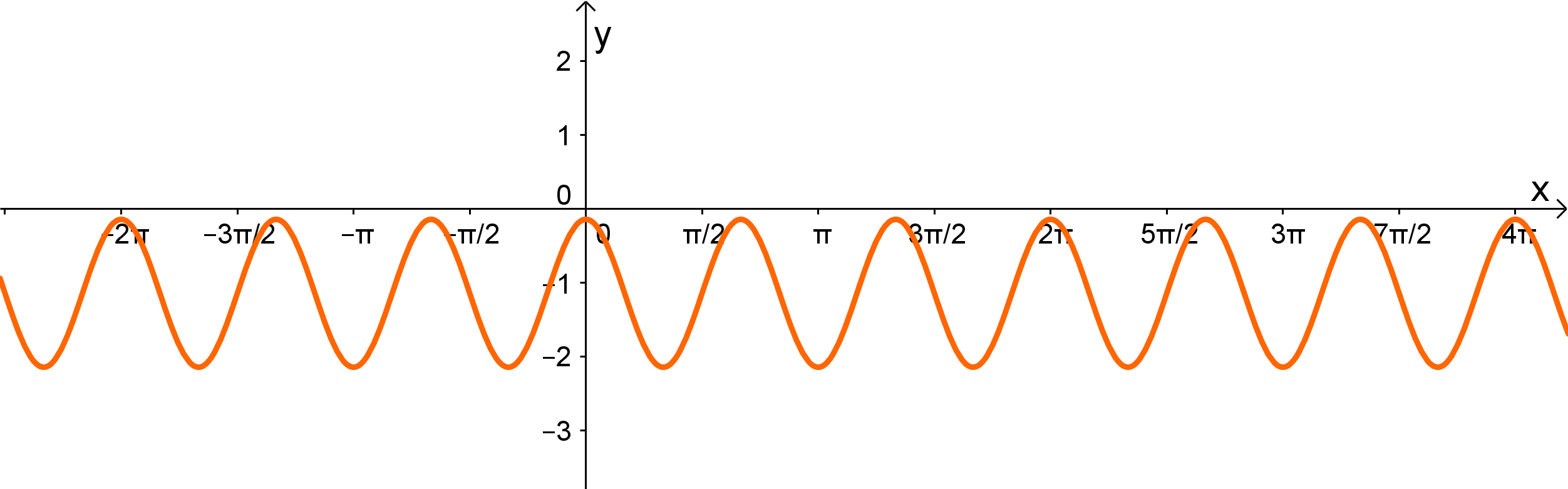
Betrachtet man den Graphen der Funktion, dann sieht man, dass der Graph achsensymmetrisch bezüglich der $yy$-Achse ist.

Betrachten der Sinus-Funktionen:

Weil die Funktion $\sin (x)\backslash sin(x)$ punktsymmetrisch ist, kann man die Funktionen $3\cdot \sin (x)3\backslash cdot\backslash sin(x)$ und $-3+2\cdot \sin (x)-3+2\backslash cdot\backslash sin(x)$ als Lösung ausschließen.

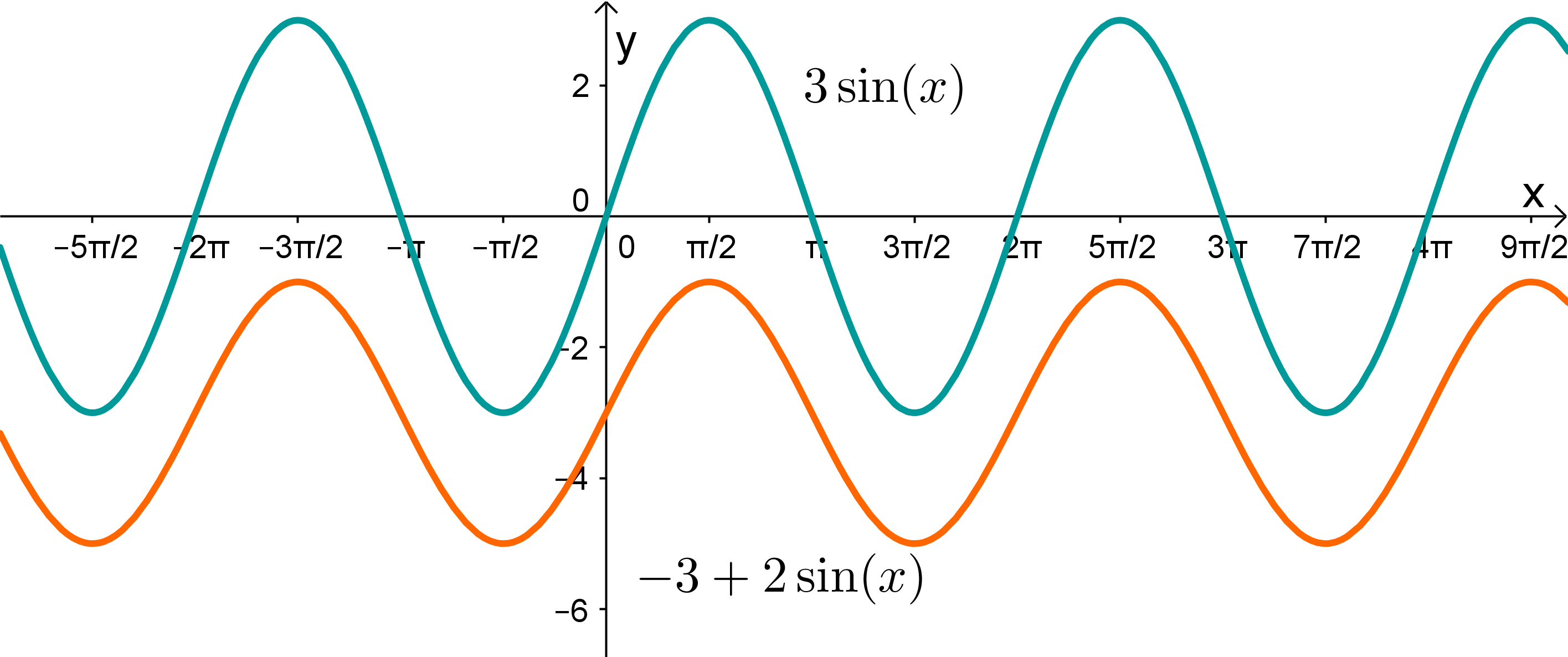
Bei $3\cdot \sin (x)3\backslash cdot\backslash sin(x)$ wird die $\sin (x)\backslash sin(x)$ Funktion in die Höhe gestreckt. Das heißt, die Funktion hat eine größere Amplitude.

Bei der Funktion $-3+2\cdot \sin (x)-3+2\backslash cdot\backslash sin(x)$ hat die $\sin (x)\backslash sin(x)$ Funktion auch eine größere Amplitude und wird zusätzlich um $33$ nach unten verschoben.

Man betrachtet also nun die beiden Kosinus-Funktionen.

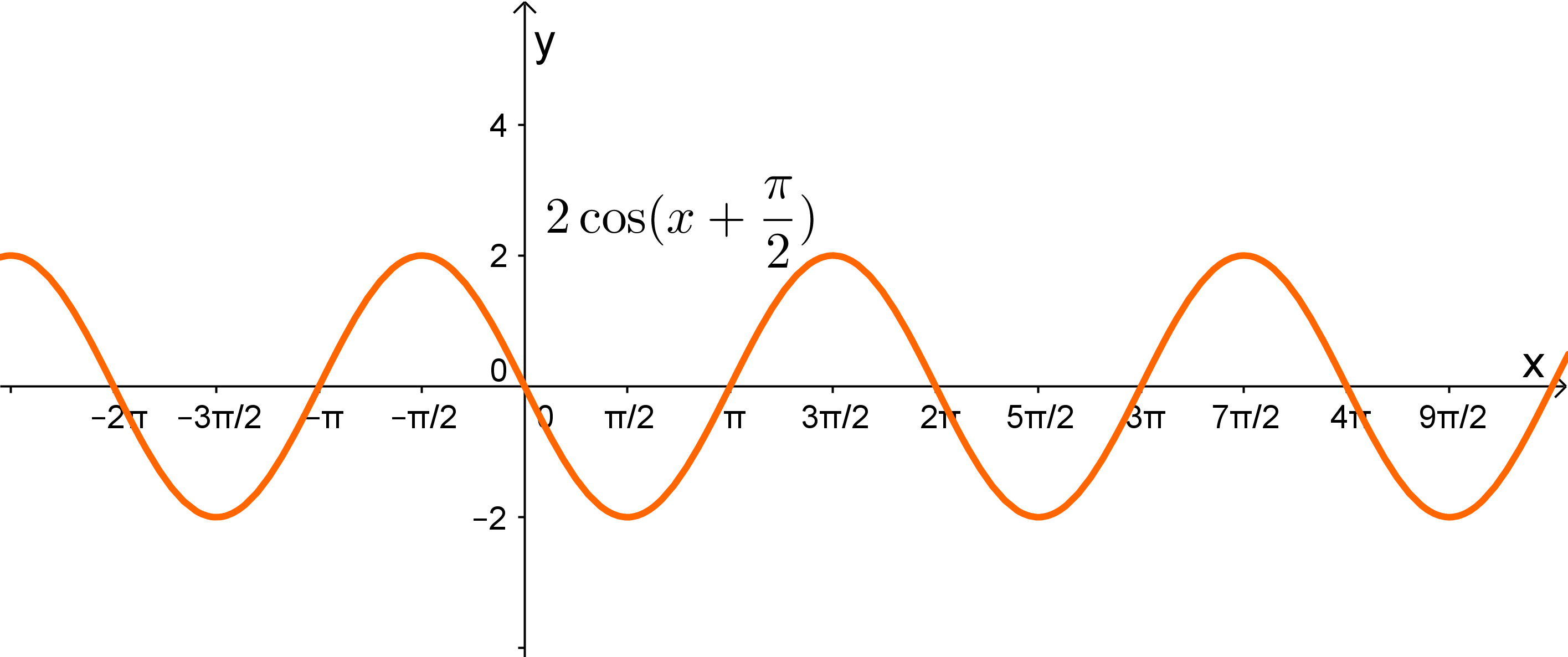
Die Funktion $2\cdot \cos (x+\frac{\pi }{2})2\backslash cdot\backslash cos(x+\backslash frac\{\backslash pi\}\{2\})$ kann man ausschließen (siehe Abbildung unten). Denn sie hat eine größere Amplitude als die gesuchte Funktion des Graphen. Zusätzlich ist sie auch noch um $\frac{\pi }{2}\backslash frac\{\backslash pi\}\{2\}$ nach rechts verschoben, die Funktion des Graphen jedoch nicht.

Die gesuchte Funktion ist also $2+\cos (3\cdot x)-\pi 2+\backslash cos(3\backslash cdot\; x)-\backslash pi$, da sie eine veränderte Periode hat und zusätzlich um $2-\pi 2-\backslash pi$ nach unten verschoben ist ($2-\pi \approx -\mathrm{1,141}2-\backslash pi\backslash approx\; -1\{,\}141$).

Veranschaulichung der ausgeschlossenen Funktion $2\cdot \cos (x+\frac{\pi }{2})2\backslash cdot\backslash cos(x+\backslash frac\{\backslash pi\}\{2\})$