Aufgaben zu Ableitungen, Symmetrie und Umkehrfunktionen trigonometrischer Funktionen

Aufgaben
Bilde die Ableitung zu folgenden Funktionen:
Kommentieren
f(x)=−sin⁡(x)\displaystyle f(x)=-\sin(x)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

f(x)=−sin⁡(x)\displaystyle f(x)=-\sin(x)
Bilde die Ableitung nach x, beachte hierzu die Ableitungsregeln vom Sinus
f(x)′=(−sin⁡(x))′=−cos⁡(x)\begin{array}{rcl} f(x)'&=&(-\sin(x))' \\\\&=&-\cos(x) \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
g(x)=sin⁡(2⋅x)\displaystyle g(x)=\sin(2\cdot x)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

g(x)=sin⁡(2⋅x)\displaystyle g(x)=\sin(2\cdot x)
Leite nach x ab, beachte hierbei die Ableitungsregel des Sinus und die Kettenregel, u(v(x))=u′(v(x))⋅v′(x)u(v(x))=u'(v(x))\cdot v'(x) mit u(x)=sin⁡(x)u(x)=\sin(x) und v(x)=2⋅xv(x)=2\cdot x
g(x)′=(sin⁡(2⋅x))′=(cos⁡(2⋅x))⋅(2⋅x)′=2⋅cos⁡(2⋅x)\begin{array}{rcl} g(x)'&=&(\sin(2\cdot x))' \\\\&=& (\cos(2\cdot x)) \cdot (2\cdot x)' \\\\&=& 2\cdot \cos(2\cdot x) \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
h(x)=(cos⁡(2⋅x))2\displaystyle h(x)=\left( \cos(2\cdot x) \right)^2

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

h(x)=(cos⁡(2⋅x))2\displaystyle h(x)=(\cos(2\cdot x))^2
Leite die Klammer ab und wende die Kettenregel an: u(v(x))=u′(v(x))⋅v′(x)u(v(x))=u'(v(x))\cdot v'(x) mit u(x)=x2u(x)=x^2 und v(x)=cos⁡(x)v(x)=\cos(x)
h(x)′=((cos⁡(2⋅x))2)′=2⋅(cos⁡(2⋅x))1⋅(cos⁡(2⋅x))′\begin{array}{rcl} h(x)'&=& ((\cos(2\cdot x))^2)' \\\\&=& 2\cdot (\cos(2\cdot x))^1\cdot (\cos(2\cdot x))' \end{array}
Leite cos⁡(2⋅x)\cos(2\cdot x) mit Hilfe der Kettenregel ab, wobei u(x)=cos⁡(x)u(x)=\cos(x) und v(x)=2⋅xv(x)=2\cdot x.
h(x)′=2⋅(cos⁡(2⋅x))1⋅(−sin⁡(2⋅x))⋅2=4⋅cos⁡(2⋅x)⋅(−sin⁡(2⋅x))\begin{array}{rcl} h(x)'&=&2\cdot (\cos(2\cdot x))^1\cdot (-\sin(2\cdot x))\cdot 2 \\\\&=&4\cdot \cos(2\cdot x)\cdot (-\sin(2\cdot x)) \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
i(x)=3⋅cos⁡(2⋅x2)\displaystyle i(x)=3\cdot \cos(2\cdot x^2)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

i(x)=3⋅cos⁡(2⋅x2)\displaystyle i(x)=3\cdot \cos(2\cdot x^2)
Leite den Kosinus mit Hilfe der Kettenregel u(v(x))=u′(v(x)⋅v′(x)u(v(x))=u'(v(x)\cdot v'(x) ab, wobei u(x)=cos⁡(x)u(x)=\cos(x) und v(x)=2⋅x2v(x)=2\cdot x^2.
i(x)′=(3⋅cos⁡(2⋅x2))′=3⋅(−sin⁡(2⋅x2))⋅(2⋅x2)′\begin{array}{rcl} i(x)'&=&(3\cdot \cos(2\cdot x^2))' \\\\&=&3\cdot (-\sin(2\cdot x^2))\cdot (2\cdot x^2)' \end{array}
Leite 2⋅x22\cdot x^2 ab.
i(x)′=−3⋅sin⁡(2⋅x2)⋅4⋅x=−12⋅x⋅sin⁡(2⋅x2)\begin{array}{rcl} i(x)'&=&-3\cdot \sin(2\cdot x^2)\cdot 4\cdot x \\\\&=&-12\cdot x\cdot \sin(2\cdot x^2) \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
t(a)=3⋅a2+4⋅sin⁡(3⋅a2)\displaystyle t(a)=3\cdot a^2+4\cdot \sin(3\cdot a^2)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

Gegeben: t(a)=3⋅a2+4⋅sin⁡(3⋅a2)t(a)=3\cdot a^2+4\cdot \sin(3\cdot a^2)
Gesucht: t′(a)t'(a)
Der vordere Term stellt ein Polynom dar und die Ableitung ist (3⋅a2)′=6⋅a(3 \cdot a^2)'=6 \cdot a. Leite den zweiten Term mit der Kettenregel ab.
(4⋅sin⁡(3⋅a2))′=4⋅cos⁡(3⋅a2)⋅6⋅a(4 \cdot \sin(3 \cdot a^2))'=4 \cdot \cos(3 \cdot a^2) \cdot 6 \cdot a
Führe die beiden Ergebnisse zusammen und erhalte die Ableitung von t(a)t(a).
t′(a)=6⋅a+24⋅a⋅cos⁡(3⋅a2)t'(a)=6 \cdot a + 24 \cdot a \cdot \cos(3 \cdot a^2)
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
j(b)=b2⋅tan⁡(b) fu¨r b∈]−π2,π2[\displaystyle j(b)=b^2 \cdot \tan(b) ~\text{für } b \in \left] -\frac{\pi}{2}, \frac{\pi}{2} \right[

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

Gegeben: j(b)=b2⋅tan⁡(b)j(b)=b^2 \cdot \tan(b)
Gesucht: j′(b)j'(b)
Da j(b)j(b) das Produkt von b2b^2 und tan⁡(b)\tan(b) ist, verwende die Produktregel, hier: j(b)=u(b)⋅v(b)j(b)=u(b)\cdot v(b) mit u(b)=b2u(b)=b^2 und v(b)=tan⁡(b)v(b)=\tan(b).
j′(b)=(b2)′⋅tan⁡(b)+b2⋅(tan⁡(b))′\begin{array}{rcl} j'(b)&=&(b^2)'\cdot\tan(b)+b^2 \cdot(\tan(b))' \end{array}
j′(b)=2⋅b⋅tan⁡(b)+b2cos⁡2(b)\begin{array}{rcl} j'(b)&=&2 \cdot b \cdot \tan(b)+\dfrac{b^2}{\cos^2(b)} \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
k(m)=1sin⁡(m) fu¨r m∈]0,π[\displaystyle k(m)=\dfrac{1}{\sin(m)} ~\text{für } m \in ]0,\pi[

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

Gegeben: k(m)=1sin⁡(m)k(m)=\dfrac{1}{\sin(m)}
Gesucht: k′(m)k'(m)
Da die Funktion einen Quotient darstellt, nämlich k(m)=u(m)v(m)k(m)=\dfrac{u(m)}{v(m)} mit u(m)=1u(m)=1 und v(m)=sin⁡(m)v(m)=\sin(m), ist die Quotientenregel anwendbar.
k′(m)=0⋅sin⁡(m)−1⋅cos⁡(m)(sin⁡(m))2=−cos⁡(m)sin⁡2(m)\begin{array}{rcl} k'(m)&=&\dfrac{0\cdot \sin(m)-1\cdot \cos(m)}{(\sin(m))^2} \\\\&=& -\dfrac{\cos(m)}{\sin^2(m)} \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
n(x)=sin⁡(cos⁡(x))\displaystyle n(x)=\sin(\cos(x))

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitungen zu trigonometrischen Funktionen

Gegeben: n(x)=sin⁡(cos⁡(x))n(x)=\sin(\cos(x))
Gesucht: n′(x)n'(x)
Die Funktion ist verkettet, es gilt nämlich n(x)=u(v(x))n(x)=u(v(x)) für u(y)=sin⁡(y)u(y)=\sin(y) und v(x)=cos⁡(x).v(x)=\cos(x). Wende daher die Kettenregel an.
n′(x)=u′(v(x))⋅v′(x)\begin{array}{rcl} n'(x)&=&u'(v(x)) \cdot v'(x) \end{array}

Leite u(y)u(y) und v(x)v(x) ab.
u′(y)=cos⁡(y)u'(y)=\cos(y) und v′(x)=−sin⁡(x)v'(x)=-\sin(x)

Setze dies in n′(x)=u′(v(x))⋅v′(x)n'(x)=u'(v(x)) \cdot v'(x) ein.
n′(x)=cos⁡(v(x))⋅(−sin⁡(x))\begin{array}{rcl} n'(x)&=&\cos(v(x)) \cdot (- \sin(x)) \end{array}

Nach oben ist v(x)=cos⁡(x)v(x)=\cos(x), setze dies ein.
n′(x)=−cos⁡(cos⁡(x))⋅sin⁡(x)\begin{array}{rcl} n'(x)&=&-\cos(\cos(x)) \cdot \sin(x) \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Prüfe, ob die folgenden Funktionen punktsymmetrisch zum Ursprung oder achsensymmetrisch zur yy-Achse sind:
Kommentieren
f(x)=2⋅cos⁡(x)+1f(x)=2\cdot \cos(x)+1

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von trigonometrischen Funktionen

Gegeben:
f(x)=2⋅cos⁡(x)+1f(x)=2\cdot \cos(x)+1
Prüfe die Funktion auf Symmetrie.
f(−x)=2⋅cos⁡(−x)+1f(-x)=2 \cdot \cos(-x)+1
f(−x)=2⋅cos⁡(x)+1=f(x)f(-x)=2 \cdot \cos(x)+1=f(x)
Daher ist f(x)f(x) ebenfalls achsensymmetrisch zur yy-Achse.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
g(x)=4⋅sin⁡(x)g(x)=4 \cdot \sin(x)


Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von trigonometrischen Funktionen

Gegeben:
g(x)=4⋅sin⁡(x)g(x)=4 \cdot \sin(x)
Prüfe die Funktion auf ihre Symmetrie.
g(−x)=4⋅sin⁡(−x)g(-x)=4 \cdot \sin(-x)
g(−x)=−4⋅sin⁡(x)=−g(x)g(-x)=-4 \cdot \sin(x)=-g(x)
Das heißt, g(x)g(x) ist punktsymmetrisch.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
h(x)=sin⁡(x−6π)h(x)=\sin(x-6\pi)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von trigonometrischen Funktionen

Gegeben:
h(x)=sin⁡(x−6π)h(x)=\sin(x-6\pi)
Da die Sinusfunktion 2π2\pi-periodisch ist, gilt sin⁡(x−6π)=sin⁡(x)\sin(x-6\pi)=\sin(x).
h(x)=sin⁡(x)h(x)=\sin(x)
Das bedeutet, dass h(x)h(x) punktsymmetrisch zum Ursprung ist, da der Sinus punktsymmetrisch zum Ursprung ist.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
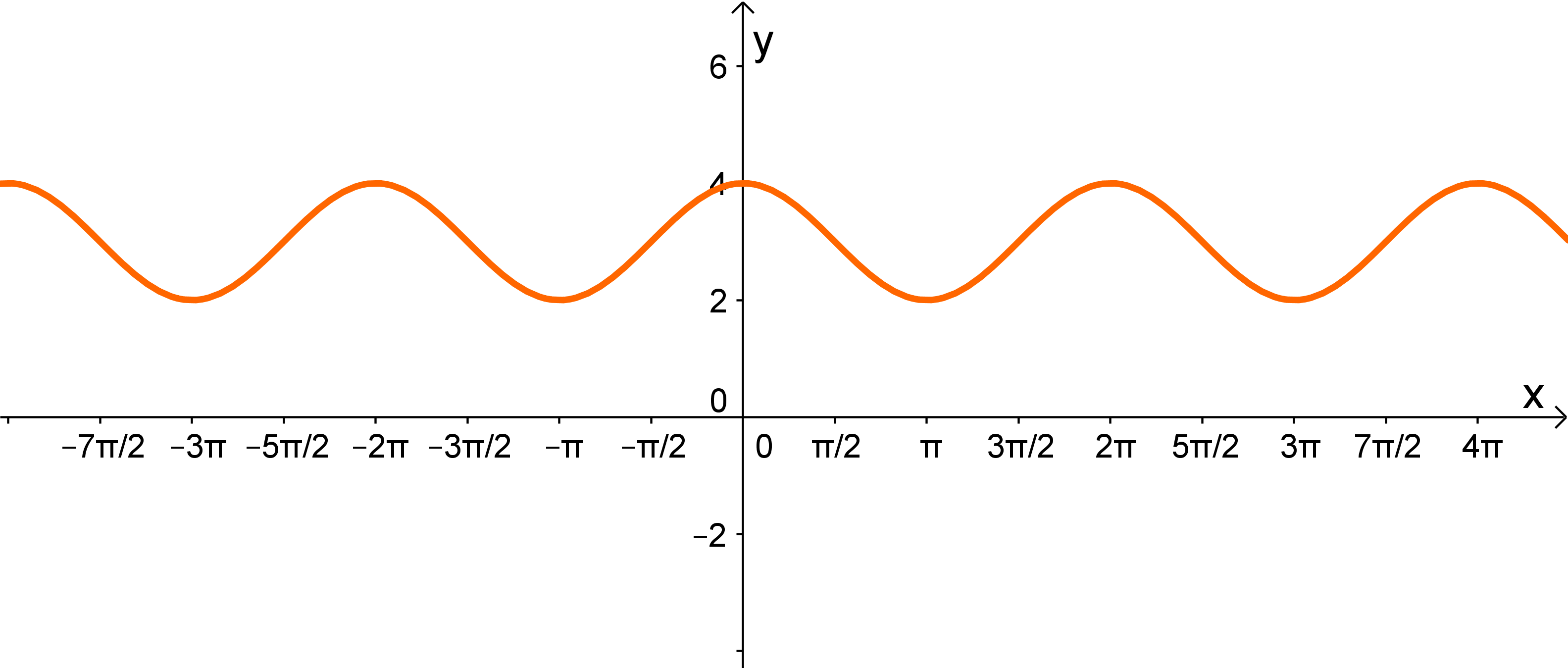
Ordne dem Graphen die richtige Funktionsgleichung zu:
Funktionsgraph
f(x)=cos⁡(x)+3f(x)=\cos(x) +3
f(x)=sin⁡(x)+3f(x)=\sin(x)+3
f(x)=cos⁡(x)−3f(x)=\cos(x) -3
f(x)=sin⁡(x)−3f(x)=\sin(x) -3

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrien von trigonometrischen Funktionen

Betrachtet man den Graphen der Funktion, sieht man, dass der Graph achsensymmetrisch bezüglich der y-Achse ist. Deshalb kann man die Funktionen sin⁡(x)+3\sin(x)+3 und sin⁡(x)−3\sin(x)-3 ausschließen, da die Sinus-Funktion punktsymmetrisch ist.
Es bleiben also die beiden Kosinus-Funktionen, die man sich anschauen muss. Die Funktion cos⁡(x)\cos(x) ist achsensymmetrisch, genau wie der Graph der gegebenen Funktion.Nachdem der Graph der Funktion die y-Achse bei y=4y=4 schneidet, kann man daraus folgern, dass die Funktion cos⁡(x)\cos(x) um 3 nach oben verschoben wurde, also cos⁡(x)+3\cos(x)+3.
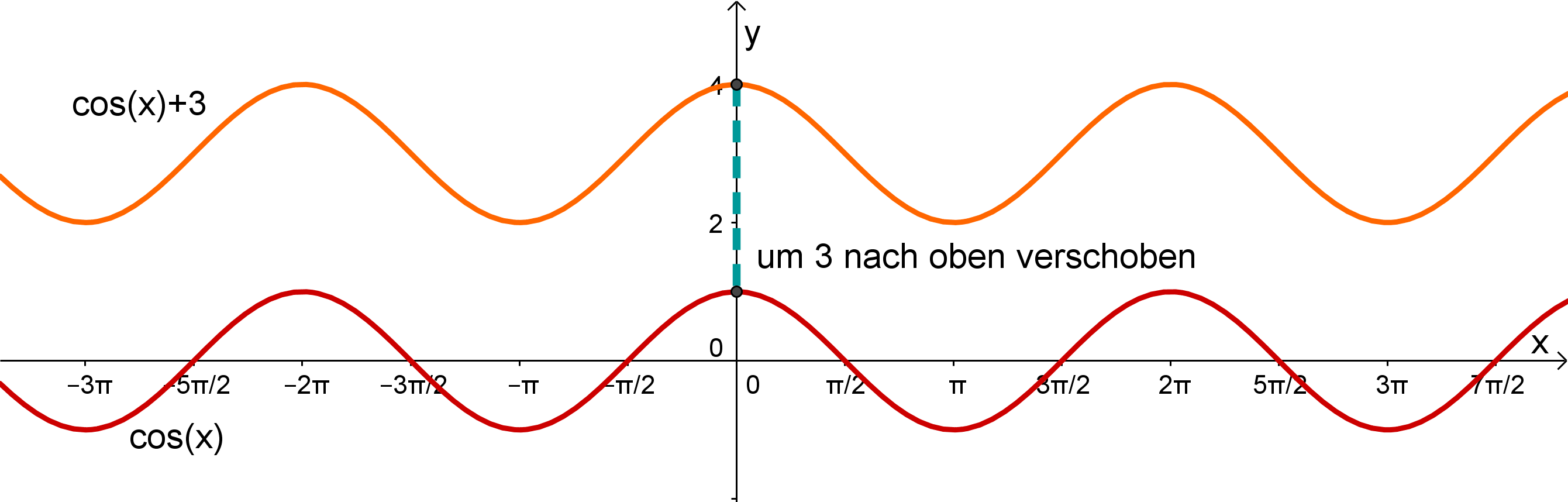
Lösungs_Graph
Somit ist f(x)=cos⁡(x)+3f(x)=\cos(x)+3 die gesuchte Funktion.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
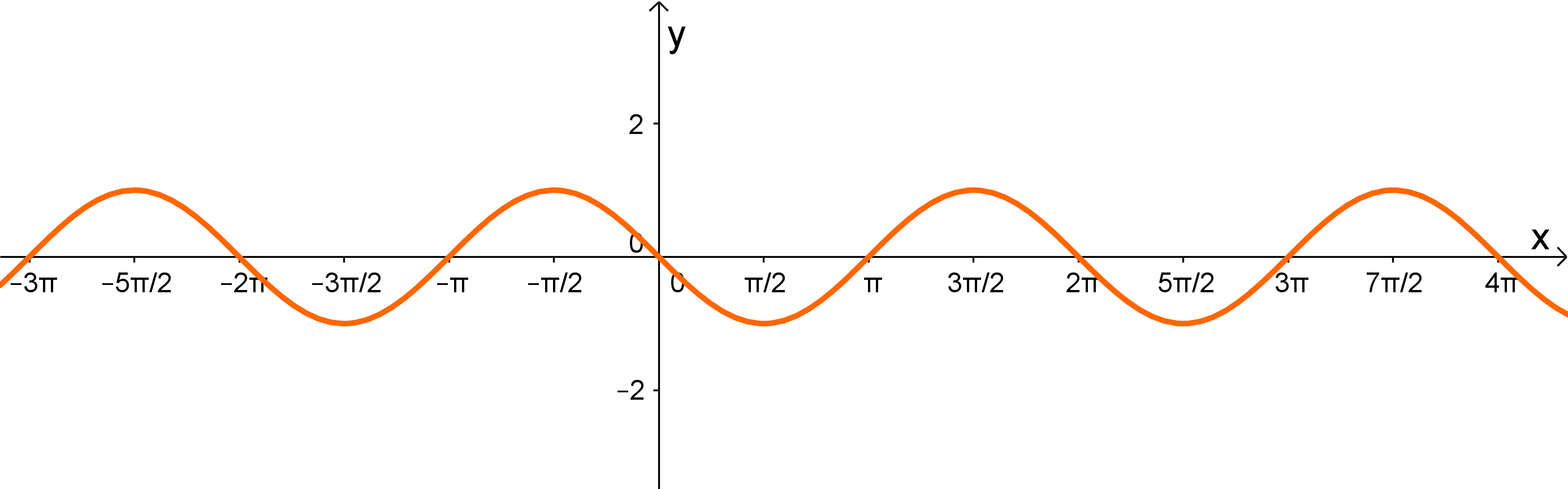
Ordne dem Graphen die richtige Funktionsgleichung zu:
Gesuchte Funktion
f(x)=sin⁡(x+π)f(x)=\sin(x+\pi)
f(x)=sin⁡(x+π2)f(x)=\sin(x+\frac{\pi}{2})
f(x)=cos⁡(2⋅x)+3⋅πf(x)=\cos(2\cdot x)+3\cdot \pi
f(x)=cos⁡(2⋅x)f(x)=\cos(2\cdot x)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrien von trigonometrischen Funktionen

Der Graph der gesuchten Funktion ist achsensymmetrisch bezüglich der y-Achse.
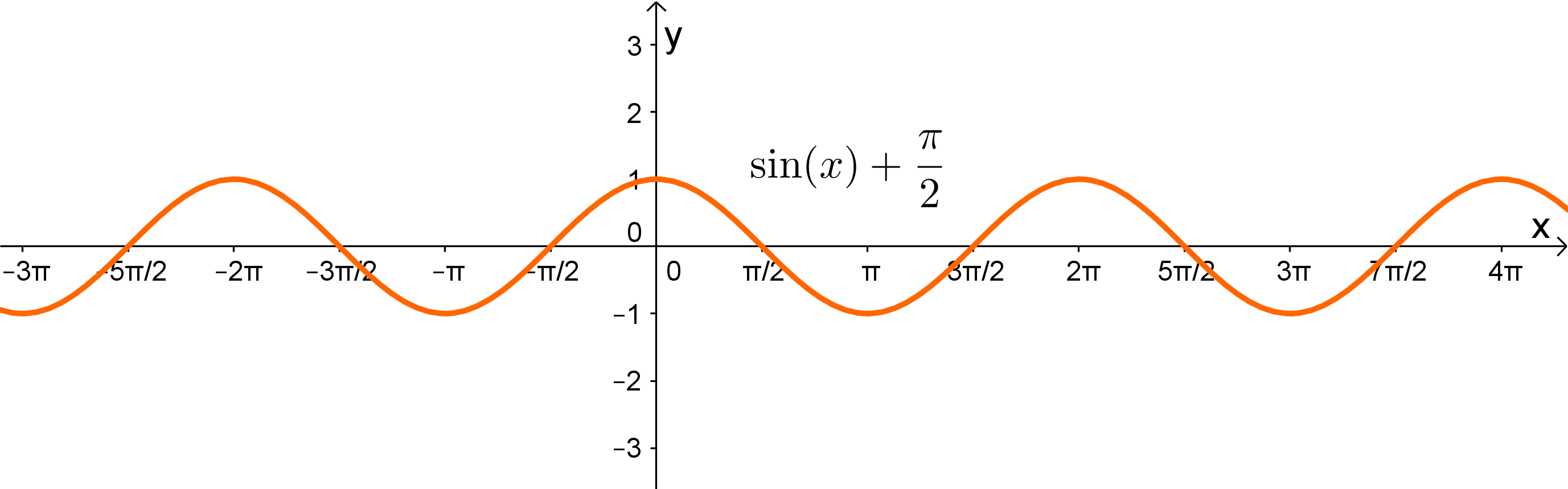
Somit kann man die beiden Funktionen cos⁡(2⋅x)\cos(2\cdot x) und cos⁡(2⋅x)+3⋅π\cos(2\cdot x)+3\cdot \pi ausschließen, denn cos⁡(2⋅x)\cos(2\cdot x) ist die Standard Kosinus-Funktion bloß mit einer größeren Periode und cos⁡(2⋅x)+3⋅π\cos(2\cdot x)+3\cdot \pi zusätzlich noch um 3⋅π3\cdot\pi nach oben verschoben.
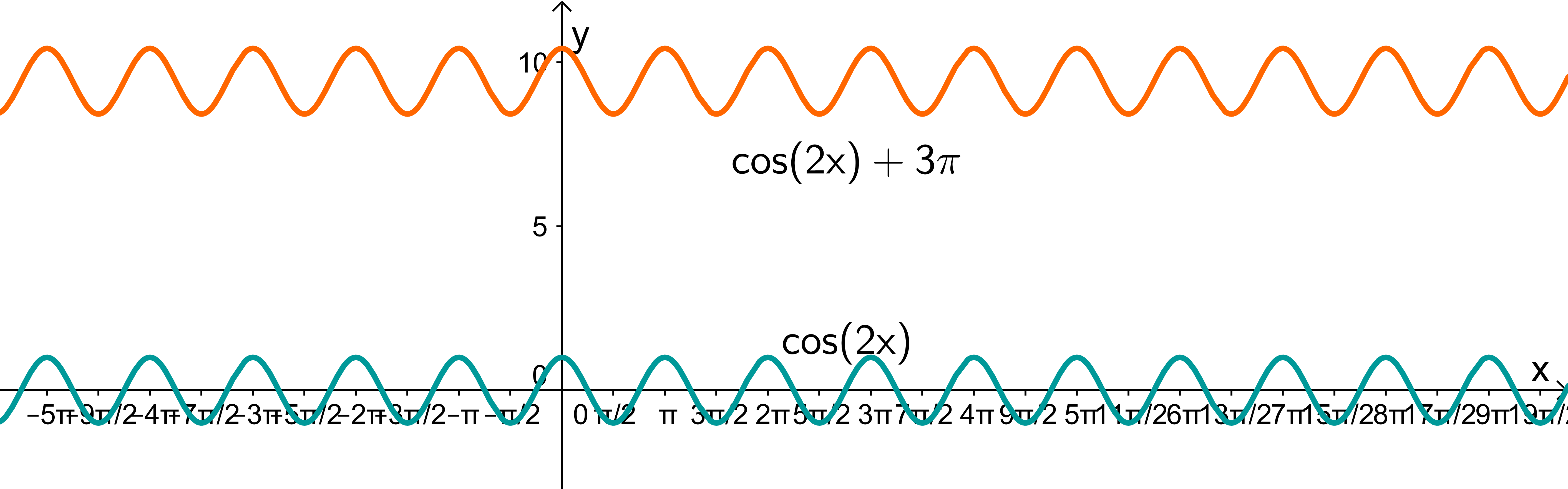
Graph zu Kosinus
Bleiben also noch die beiden Sinus-Funktionen also Lösungsmöglichkeiten.
Die Funktion sin⁡(x)\sin(x) ist punktsymmetrisch und im Intervall zwischen 00 und π\pi positiv, die Funktion des gegeben Graphen ist punktsymmetrisch und im Intervall von 00 bis π\pi negativ, also suchen wir eine Funktion die sin⁡(x)\sin(x) um eine halbe Periode verschiebt.
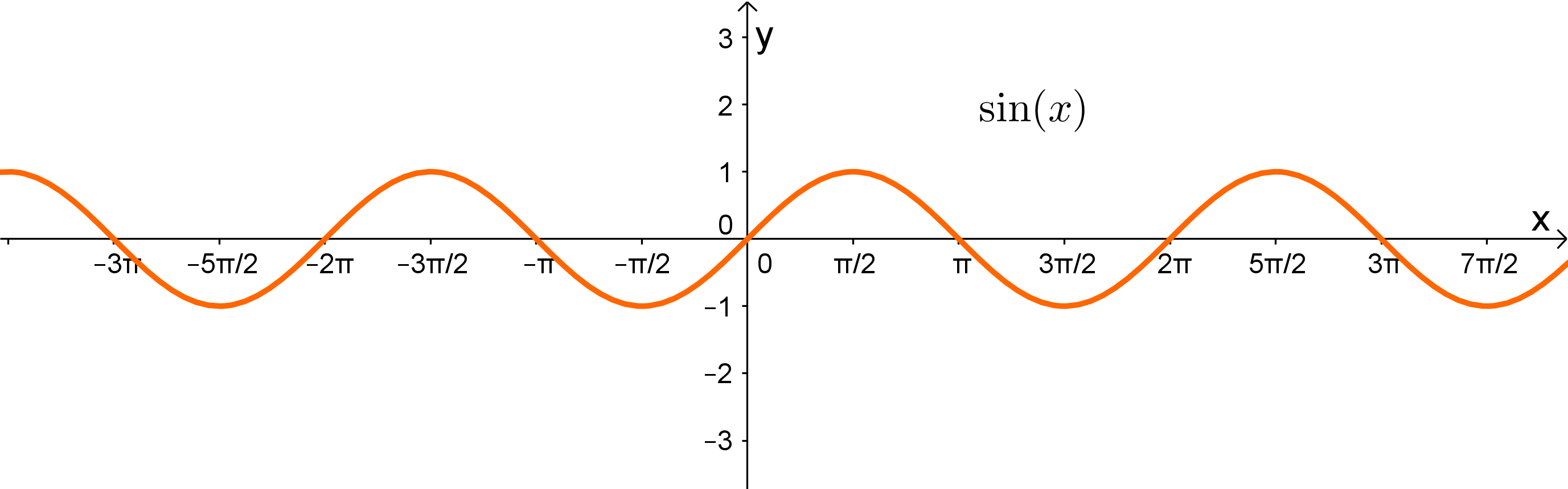
Graph zu Sinus
Da die Periode der sin(x)sin(x) Funktion 2⋅π2\cdot \pi lang ist, muss sin⁡(x)\sin(x) um π\pi verschoben werden. Darum ist die richtige Lösung sin⁡(x+π)\sin(x+\pi)
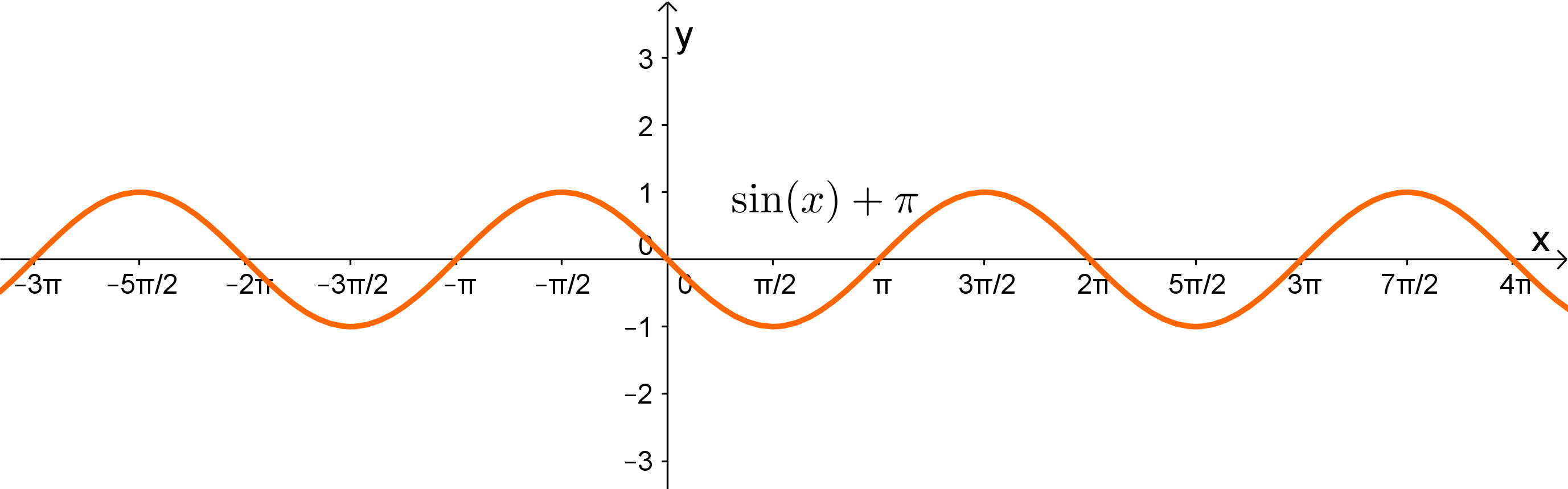
Graph zu einer Sinus Funktion
Graph zu einer Sinus Funktion
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Ordne dem Graphen die richtige Funktionsgleichung zu:
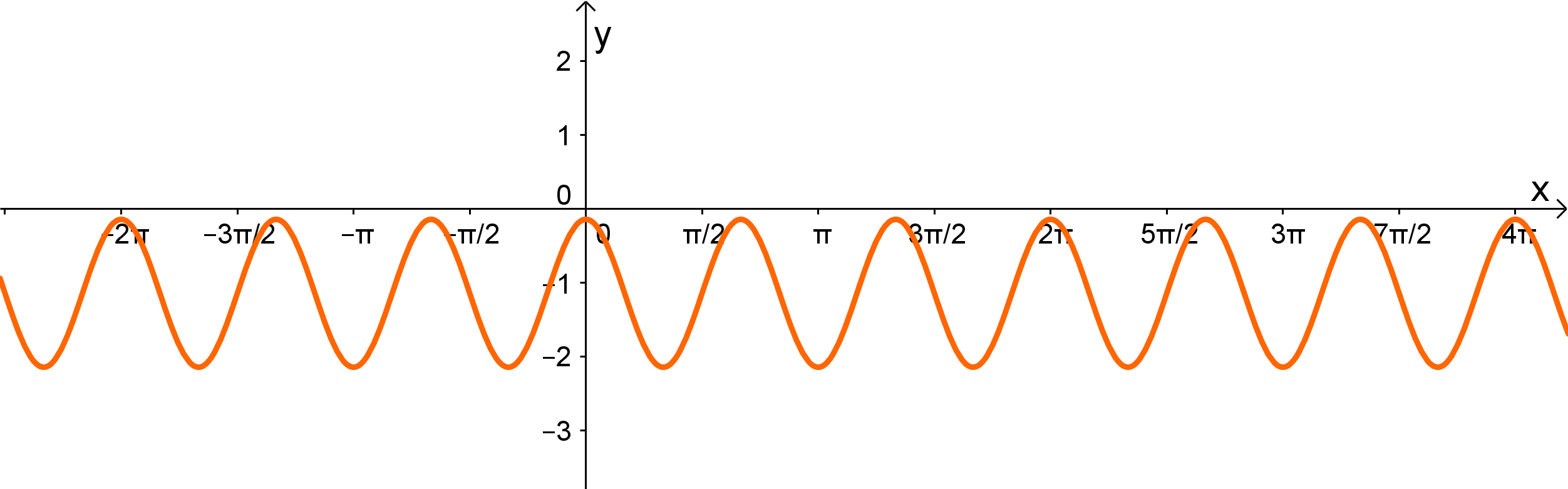
Graph zu Aufgabe
f(x)=2+cos⁡(3⋅x)−πf(x)=2+\cos(3\cdot x)-\pi
f(x)=3⋅sin⁡(x)f(x)=3\cdot \sin(x)
f(x)=2⋅cos⁡(x+π2)f(x)=2\cdot\cos(x+\frac{\pi}{2})
f(x)=−2+2⋅sin⁡(x)f(x)=-2+2\cdot\sin(x)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrien von trigonometrischen Funktionen

Für diese Aufgabe ist es hilfreich, nach dem Ausschlussverfahren vorzugehen. (Das heißt, du überlegst dir, welche Antworten nicht richtig sein können und entscheidest dich für die einzige Antwort, die übrig bleibt.)
Überlege dir hierfür:
Welche Symmetrieeigenschaften hat die Funktion?
Inwiefern wurde sie entlang der y-Achse oder der x-Achse verschoben?
Betrachtet man den Graphen der Funktion, dann sieht man, dass der Graph achsensymmetrisch bezüglich der yy-Achse ist.
Betrachten der Sinus-Funktionen:
Weil die Funktion sin⁡(x)\sin(x) punktsymmetrisch ist, kann man die Funktionen 3⋅sin⁡(x)3\cdot\sin(x) und −3+2⋅sin⁡(x)-3+2\cdot\sin(x) als Lösung ausschließen.
Bei 3⋅sin⁡(x)3\cdot\sin(x) wird die sin⁡(x)\sin(x) Funktion in die Höhe gestreckt. Das heißt, die Funktion hat eine größere Amplitude.
Bei der Funktion −3+2⋅sin⁡(x)-3+2\cdot\sin(x) hat die sin⁡(x)\sin(x) Funktion auch eine größere Amplitude und wird zusätzlich um 33 nach unten verschoben.
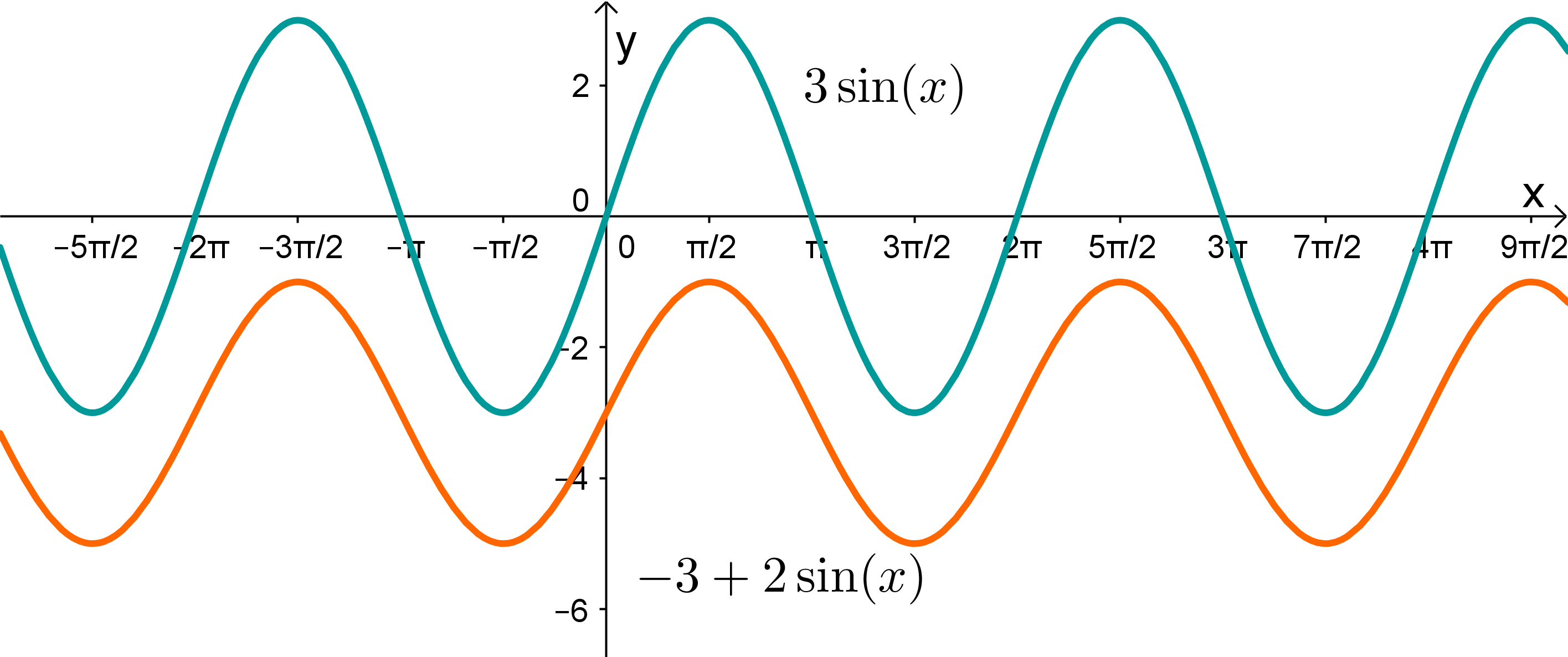
Graph Sinus
Man betrachtet also nun die beiden Kosinus-Funktionen.
Die Funktion 2⋅cos⁡(x+π2)2\cdot\cos(x+\frac{\pi}{2}) kann man ausschließen (siehe Abbildung unten). Denn sie hat eine größere Amplitude als die gesuchte Funktion des Graphen. Zusätzlich ist sie auch noch um π2\frac{\pi}{2} nach rechts verschoben, die Funktion des Graphen jedoch nicht.
Die gesuchte Funktion ist also 2+cos⁡(3⋅x)−π2+\cos(3\cdot x)-\pi, da sie eine veränderte Periode hat und zusätzlich um 2−π2-\pi nach unten verschoben ist (2−π≈−1,1412-\pi\approx -1,141).
Veranschaulichung der ausgeschlossenen Funktion 2⋅cos⁡(x+π2)2\cdot\cos(x+\frac{\pi}{2})
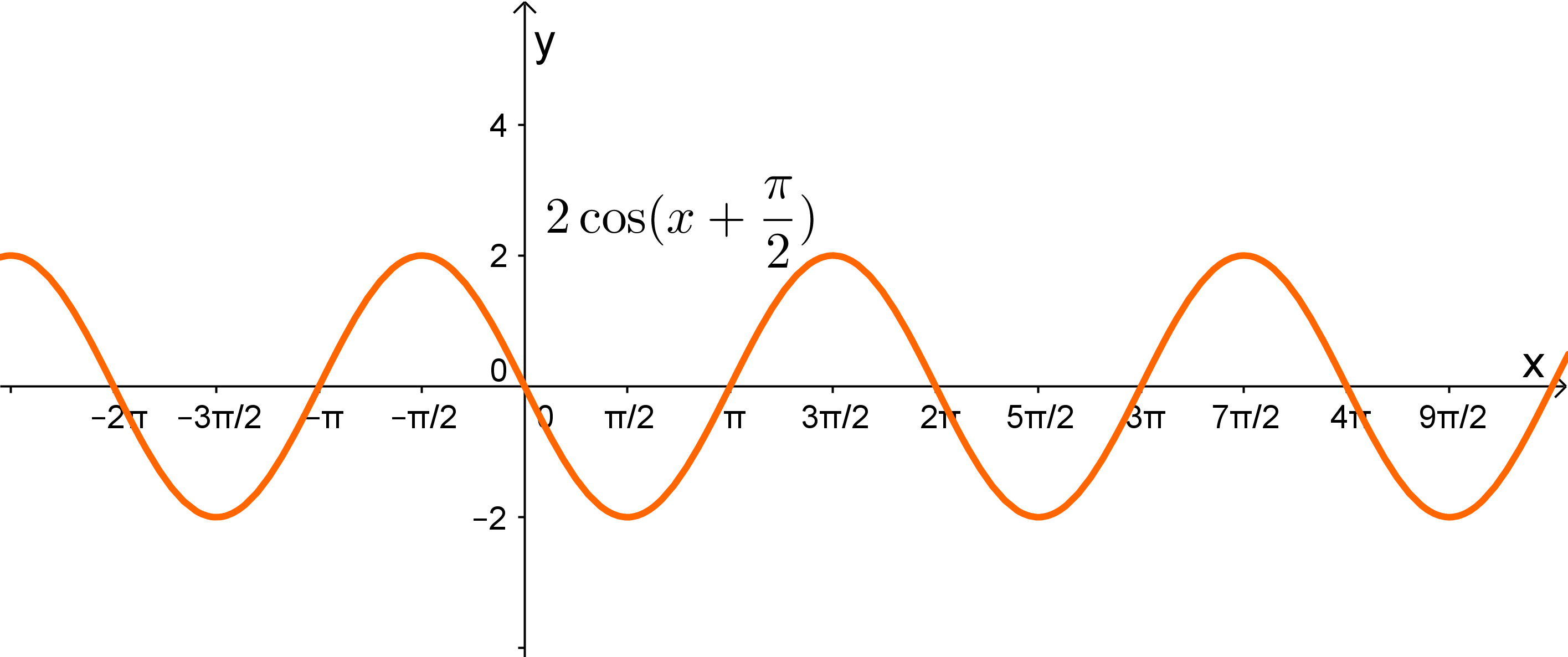
Kosinus Funktion
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Löse die folgenden Gleichungen nach xx auf:
Kommentieren
2⋅sin⁡(x−π)=12\cdot\sin(x-\mathrm\pi)=1 für x∈[−π2,π2]x \in \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Umkehrfunktiion

2⋅sin⁡(x−π)=12\cdot\sin(x-\mathrm\pi)=1
Teile auf beiden Seiten der Gleichung durch 22.
sin⁡(x−π)=12\sin(x-\pi)=\frac 12
x−π=sin⁡−1(12)x-\pi = \sin^{-1}\left(\frac 12\right)
Löse nach xx auf. Betrachte hierzu den Graphen des Arkussinus und erhalte sin⁡−1(12)=π6.\sin^{-1}\left(\frac{1}{2}\right) = \frac{\pi}{6}.
x=π+sin⁡−1(12)=π+π6=7π6\begin{array}{rcl} x &=& \pi+\sin^{-1}\left(\frac12\right) \\&=& \pi + \dfrac{\pi}{6} \\&=&\dfrac{7\mathrm\pi}6 \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
cos⁡(x−π2)=1\cos\left(x-\dfrac{\pi}{2}\right)=1 für x∈[−π2,π2]x \in \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Umkehrfunktionen



cos⁡(x−π2)=1\cos\left( x- \dfrac{\pi}{2} \right) = 1
Wende die Umkehrfunktion des Kosinus an.
x−π2=cos⁡−1(1)x-\dfrac{\pi}{2} = \cos^{-1} (1)
Betrachte den Graphen des Arkuskosinus und lese ab, dass cos⁡−1(1)=0\cos^{-1}(1)=0.
x−π2=0x-\dfrac{\pi}{2} = 0
Löse die Gleichung nun nach xx auf.
x=π2x=\dfrac{\pi}{2}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
cos⁡(x+π2−1)=0\cos\left(x+\dfrac{\pi}{2}-1\right)=0 für x∈[0,π]x \in [0,\pi]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Umkehrfunktionen

cos⁡(x+π2−1)=0\cos\left(x+\dfrac{\pi}{2}-1\right) = 0
Wende die Umkehrfunktion der Kosinusfunktion an.
x+π2−1=cos⁡−1(0)x+\dfrac{\pi}{2}-1=\cos^{-1}(0)
Betrachte den Graphen des Arkuskosinus und erhalte cos⁡−1(0)=π2.\cos^{−1}(0)=\frac{\pi}{2}.
x+π2−1=π2x+\dfrac{\pi}{2}-1=\dfrac{\pi}{2}
Löse die Gleichung nach xx auf.
x+π2−1=π2∣−π2x−1=0∣+1x=1\begin{array}{rcl} x+\dfrac{\pi}{2}-1&=&\dfrac{\pi}{2}&&|-\dfrac{\pi}{2} \\ \\x-1&=&0&&|+1 \\ \\x&=&1 \end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Kommentieren Kommentare
2
Mathewally 2020-12-05 18:39:50+0100
Das Problem mit den Definitionsbereichen der 6. Aufgabe ist seit drei Jahren offen.
Ich würde das (eventuell u.a. durch leichte Umformulierung des Aufgabentextes) richtig stellen. Dazu muss man allerdings auch einige Dinge im Artikel über "Trigonometrische Umkehrfunktionen" ergänzen, nämlich: "Wenn ich eine Lösung von $\sin x=a$ habe, wie sehen alle Lösungen aus?" und analog für Kosinus und Tanges. Ist das Schulstoff? Wenn nicht, soll das trotzdem hierhin?
Ich weiß, dass an der Uni regelmäßig solche Sachen als bekannt vorausgesetzt werden, ohne zu prüfen, ob das auch im Lehrplan steht. Von daher wäre es vielleicht nicht schlecht.
Ich mache das aber nur, wenn Leute, die sich damit auskennen, ihr OK geben.
Viele Grüße
Peter
Marc_Ho 2020-12-12 14:09:35+0100
Ich bespreche bei der Einführung von sin/cos/tan immer auch gleichzeitig arcsin, arccos und arctan. (Die Schreibweise sin^-1 mag ich gar nicht, weil sie nach einer Potenz aussieht.) Im G8 in NRW habe ich die Anzahl der Lösungen nicht ausführlich thematisiert, sondern nur angesprochen. Im G9 habe ich das allerdings immer ausführlich behandelt. Gerade durch den Einsatz von graphikfähigen Taschenrechnern ist das schnell erklärbar. Im neuen Kernlehrplan für das G9 in NRW sind der Kosinussatz und Berechnungen mit diesem verbindlich vorgesehen, also muss das in drei Jahren in Klasse 10 wieder unterrichtet werden.
Marc_Ho 2020-12-12 14:14:58+0100
In der Aufgabe 6a würde ich vorschlagen, dass tatsächlich nicht die Lösung, sondern die Aufgabenstellung verändert wird, indem das Intervall angepasst wird. Wenn du dir Mühe machen willst (im Unterricht würde ich das IMMER so machen), kannst du ja den Graphen der Sinusfunktion einbinden in die Lösung, sodass man die beiden Lösungen sofort sieht.
Antwort abschicken
0
Raufutu777 2017-08-15 13:09:40+0200
In der 6. Aufgabe wurden die Intervalle für die Lösungsmenge nicht berücksichtigt.
Renate 2017-08-16 17:19:43+0200
Hallo Raufutu777,
zunächst mal vielen Dank für deinen Kommentar, der, soweit ich erkennen kann, vom mathematischen Standpunkt her auch völlig berechtigt ist!
Leider weiß ich nicht, ob in nächster Zeit jemand von uns dazu kommt, sich der Sache anzunehmen. Ich habe es jetzt erstmal wenigstens in unser Dokument eingetragen, in dem wir solche noch zu erledigenden Aufgaben sammeln.

Hättest du vielleicht Lust, selbst eine Bearbeitung zu versuchen?

Wenn du dazu Hilfe oder Antworten auf technische Fragen oder Probleme suchst, wirst du vielleicht auf der Seite https://de.serlo.org/hilfe-startseite fündig.
Und wenn nicht, dann zögere bitte nicht, dich an uns zu wenden - zum Beispiel, indem du auf diese Diskussion hier antwortest, oder indem du einen Kommentar auf das Profil von jemanden von uns (https://de.serlo.org/team) schreibst.

Viele Grüße
Renate
Antwort abschicken