Periode (einer Funktion)

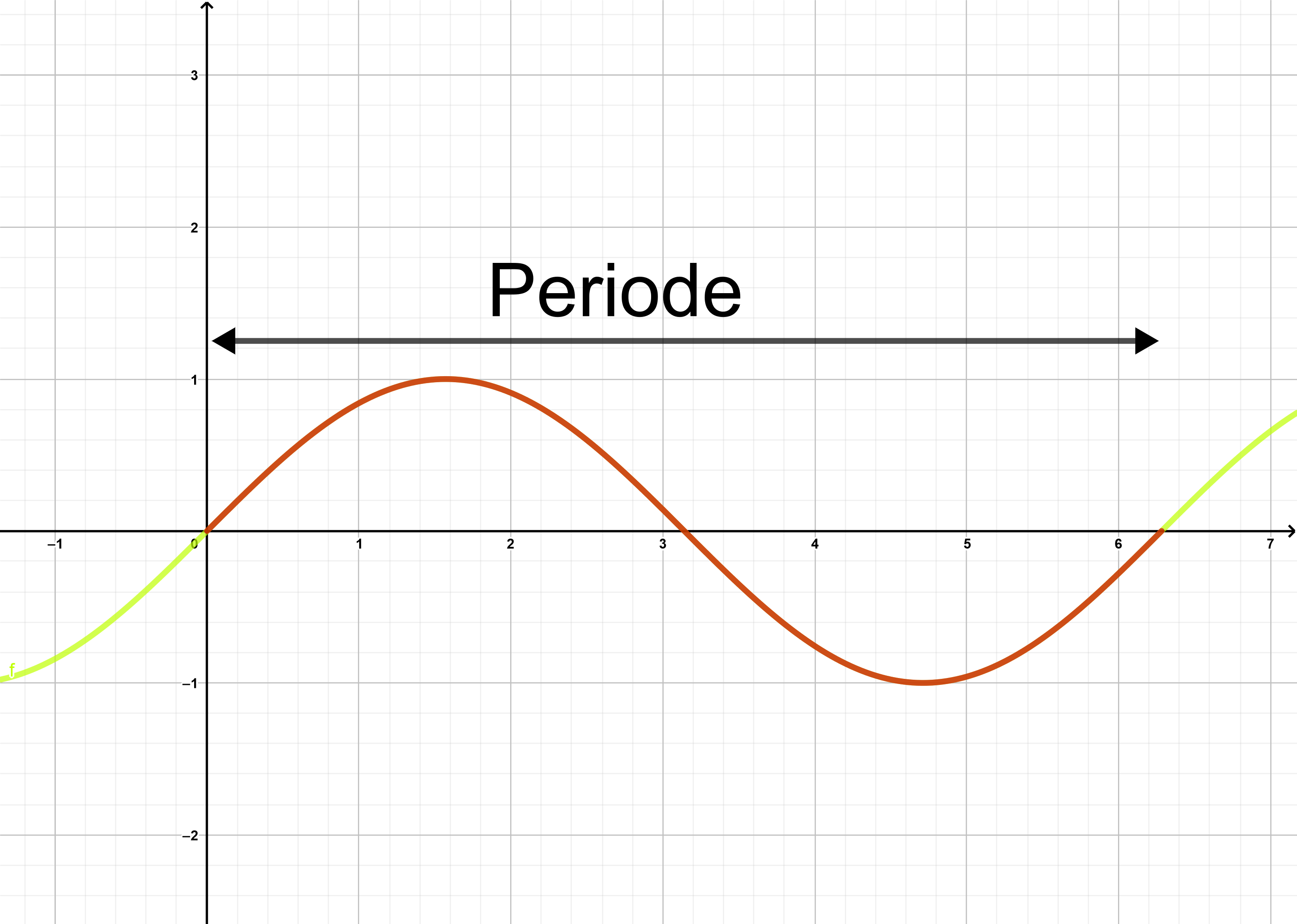
Beispiel

Ein Beispiel einer periodischen Funktion ist die Sinusfunktion.

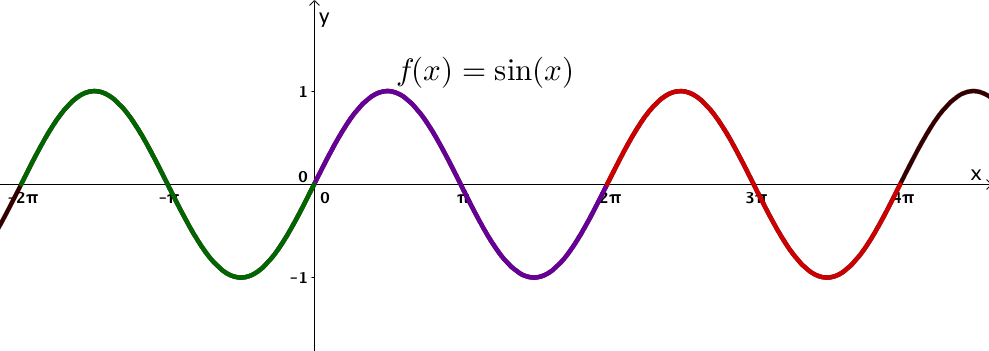
An dem Graphen erkennt man (auch anhand der Farben), dass sich $\sin (x)$ im Abstand von $2\mathrm{\pi }$ wiederholt. Das heißt, die Sinusfunktion besitzt die Periode $2\pi$.

Startet man an einer beliebigen Stelle $x$, kann man beliebig oft $2\pi$ addieren/subtrahieren und der Funktionswert des Sinus bleibt derselbe. Zum Beispiel:

$\sin (0)=\sin (4\pi )=\sin (-2\pi )$

$\sin (1)=\sin (1+2\pi )=\sin (1+24\pi )$

Das selbe gilt auch für die Kosinusfunktion.

Formel

Falls eine Funktion $f$ die Periode $p$ besitzt, dann gilt

$f\left(x\right)=f(x+p)=f(x+2p)=f(x+3p)=\dots$

und $f(x)=f(x-p)=f(x-2p)=f(x-3p)=\dots$

Hieran erkennt man, dass man zu jedem $x$ ein Vielfaches der Periode $p$ addieren/subtrahieren kann und der Funktionswert bleibt dabei derselbe.

Eigenschaften

• Die verschobenen und gestreckten Sinus- und Kosinusfunktionen können durch $a\cdot \sin (b\cdot (x+c))+d$ und $a\cdot \cos (b\cdot (x+c))+d$ dargestellt werden. Sie besitzen jeweils die Periode $p=\frac{2\pi }{|b|}$.

• Eine Funktion mit Periode $p$ wiederholt sich ebenfalls auch alle $2p,3p,\dots$. Als Periode bezeichnet man aber den kleinsten Wert mit dieser Eigenschaft.

• Besitzt eine Funktion die Periode $p$, dann spricht man davon, dass die Funktion $p$-periodisch ist.  

• Man sagt, der Graph einer periodischen Funktion ist verschiebungssymmetrisch mit ihrer Periode.

• Addiert man zwei Funktionen mit verschiedenen Perioden, dann ist das kleinste gemeinsame Vielfache der beiden Perioden die Periode der neuen Funktion.

• Den Kehrwert der Periode, also $\frac{1}{p}$, nennt man auch Frequenz.