Die Vierfeldertafel wird bei einem Zufallsexperiment mit zwei unterschiedlichen Ereignissen verwendet.
Mit ihr kann man leicht Verknüpfungen zwischen den Ereignissen darstellen und so auf unterschiedliche absolute oder relative Häufigkeiten schließen.
In diesem Artikel wird die Verwendung der Vierfeldertafel mit der absoluten und der relativen Häufigkeit erklärt. Der Artikel Vierfeldertafel beschreibt den Umgang mit Wahrscheinlichkeiten.

Wenn in einer Vierfeldertafel genügend Einträge da sind, ist es sehr leicht, die fehlenden Werte zu ergänzen.
Vierfeldertafel mit absoluten Häufigkeiten
An einem Beispiel wird die Vierfeldertafel nun erklärt.
Beispiel
In einer Vorlesung befinden sich normalerweise 50 Studierende. Da es gestern aber sehr kalt war, sind heute fünf Studierende krank. Gestern haben 40 Studierende eine Mütze getragen. Von diesen Mützenträgern sind heute 38 erschienen.
Wie viele Studierende, die gestern keine Mütze getragen haben, sind heute krank? Und wie viele Studierende, die heute anwesend - also gesund - sind, haben gestern keine Mütze getragen?
1. Ereignisse bzw. Merkmale herausfinden
Beispiel | Allgemein |
|---|---|
In diesem Beispiel kommen zwei Merkmale vor: Mütze tragen und krank sein, sowie deren Gegenteile: keine Mütze tragen und nicht krank sein Dann kann man diese gleich in die Vierfeldertafel schreiben. | Man braucht immer zwei Ereignisse/Merkmale. Oft werden diese mit Buchstaben abgekürzt. Zum Beispiel und . Die Gegenteile werden meistens mit einem Strich geschrieben: nicht : und nicht : |
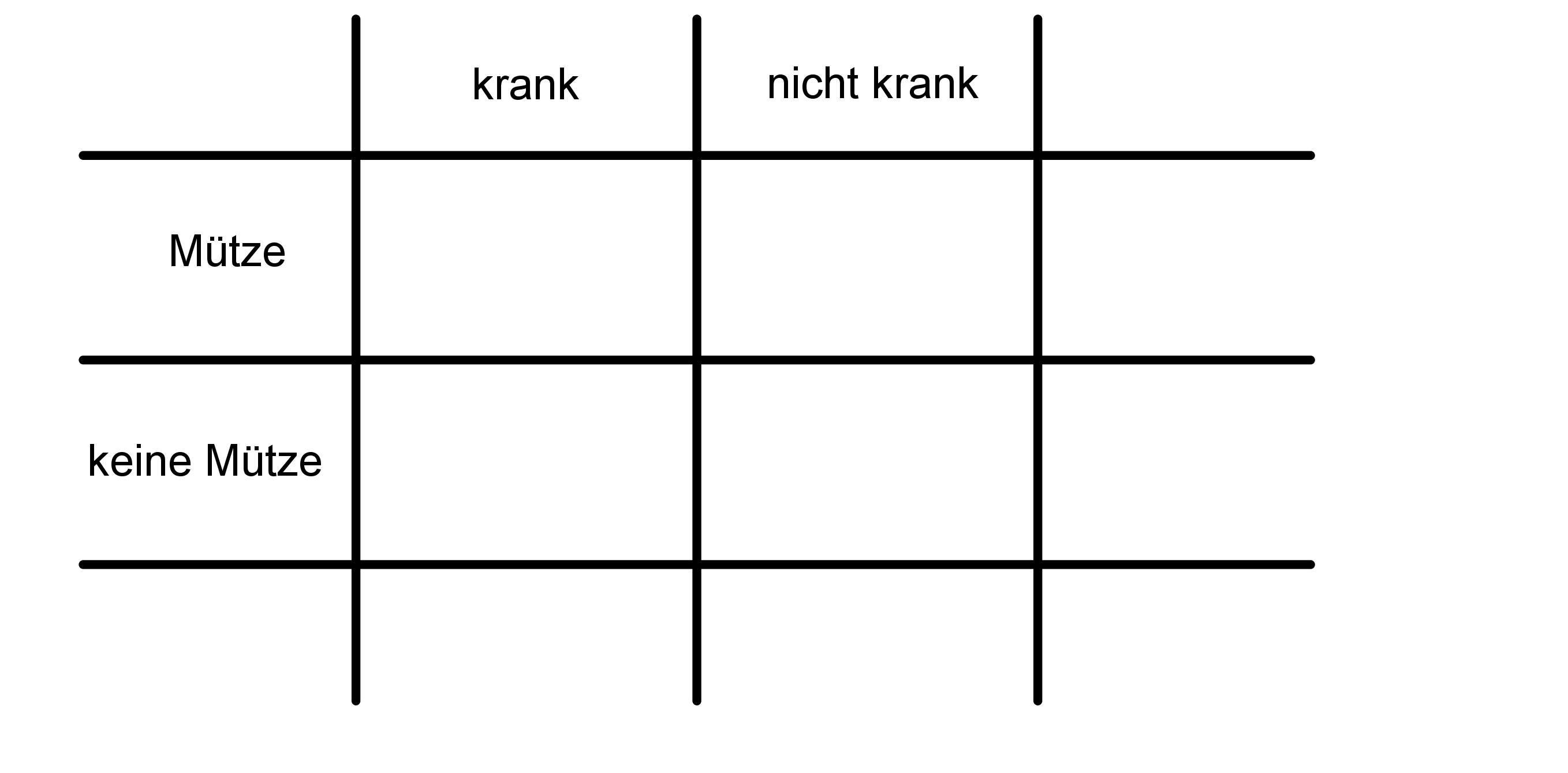 | 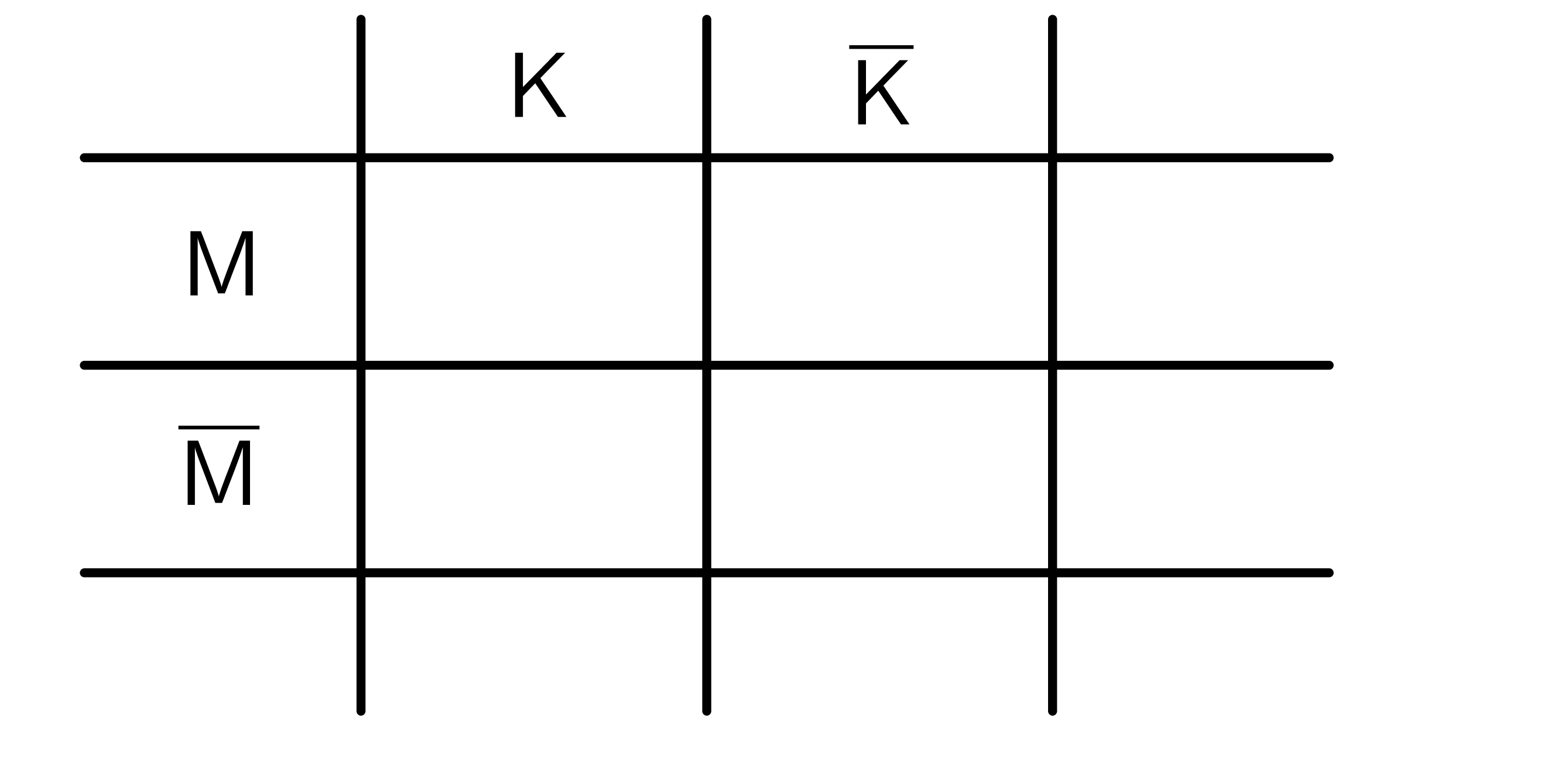 |
2. Bekannte Häufigkeiten zuordnen
Gesamtzahl: 50
Kranke Studierende: 5
Studierende, die gestern eine Mütze auf hatten: 40
Studierende*r hatte gestern Mütze auf und ist heute erschienen, also gesund: 38
3. In die Vierfeldertafel einordnen
Die einzelnen Ereignisse/Merkmale bzw. deren Häufigkeiten müssen nun den richtigen Feldern der Vierfeldertafel zugeordnet werden.
In der Spalte ganz rechts kommen die Häufigkeiten des einen Merkmals und in die unterste Zeile kommen die Häufigkeiten des anderen Merkmals/Ereignisses. Ganz unten rechts steht immer die Gesamtzahl. In den vier Felder in der Mitte stehen die jeweiligen Kombinationen.

Beispiel | Allgemein |
|---|---|
 |  |
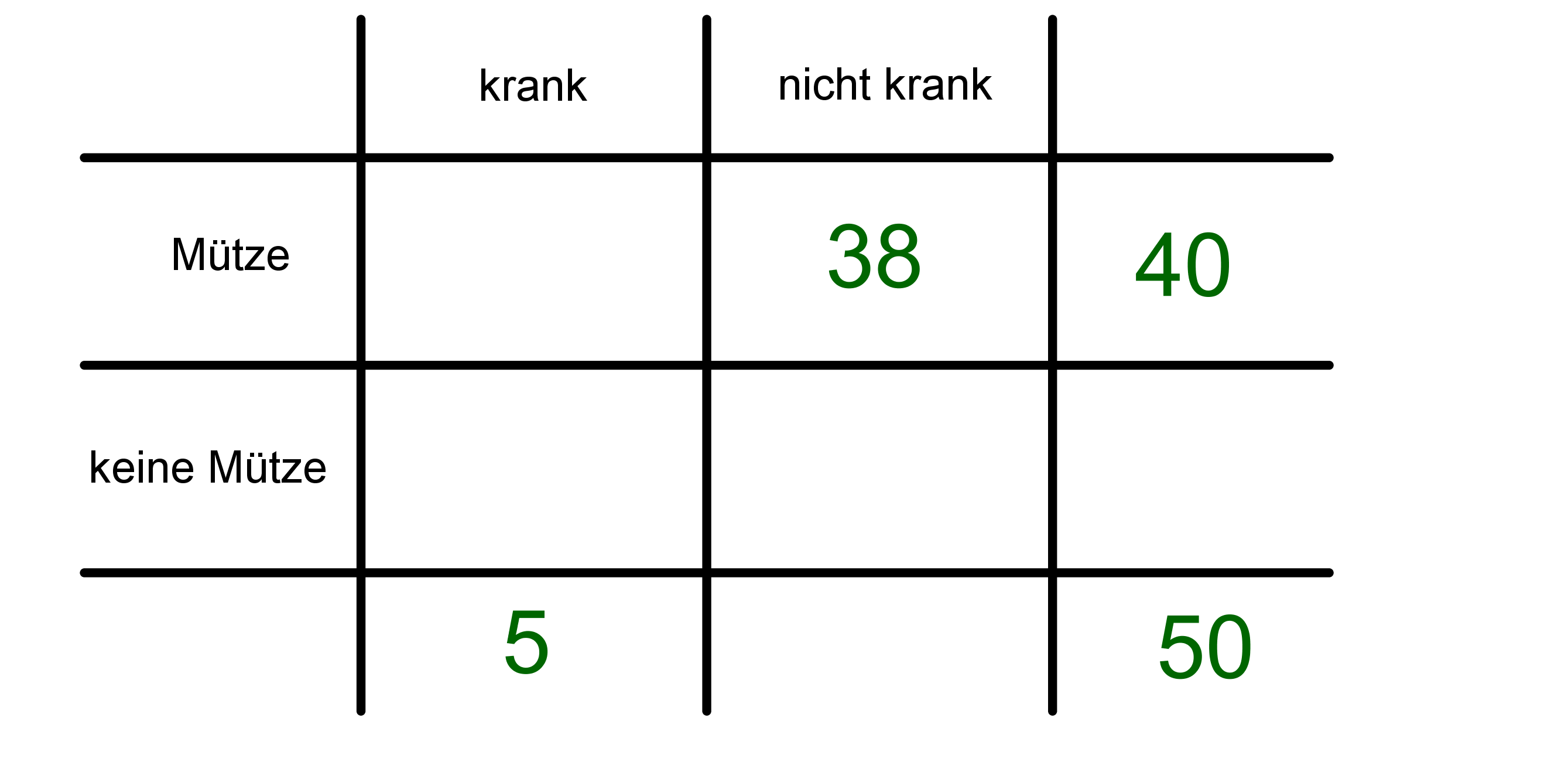 |
4. Restliche Felder ausrechnen
Der letzte Wert einer Zeile ergibt immer die Summe der beiden vorherigen Werte der Zeile. Ebenso ergibt der letzte Wert einer Spalte die Summe der vorherigen Werte der Spalte. Für die erste Zeile bedeutet das in unserem Beispiel:
Mit den bekannten Werten ergibt sich somit:
Auf diese Art und Weise kann man nach und nach die gesamt Vierfeldertafel ausfüllen.
Beispiel | Allgemein |
|---|---|
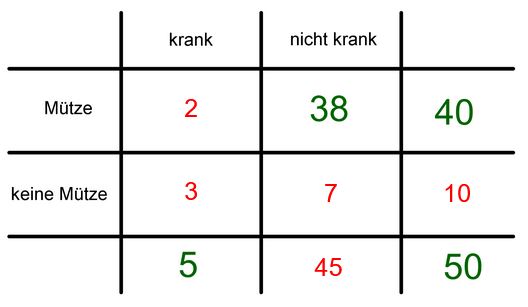 | 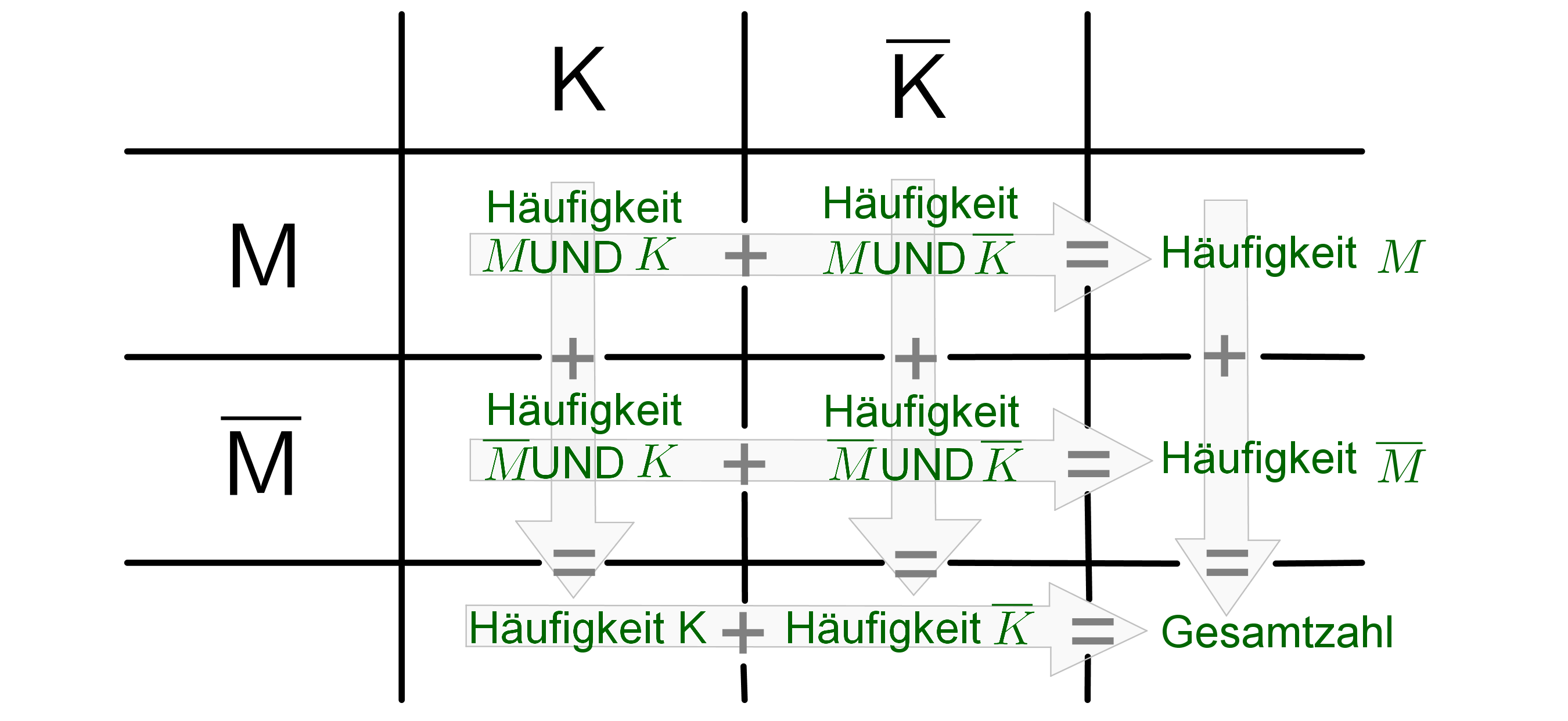 |
In der ausgefüllten Vierfeldertafel stehen die absoluten Häufigkeiten der jeweiligen Ereignisse, die absoluten Häufigkeiten der kombinierten Ereignisse sowie die Gesamtzahl.
Vierfeldertafel mit relativen Häufigkeiten
Die Vierfeldertafel kann ebenso verwendet werden, um darzustellen, wie relative Häufigkeiten miteinander verknüpft sind.
Dies wird an dem obigen Beispiel gezeigt.
1. Ereignisse bzw. Merkmale herausfinden
Dieser Schritt läuft genauso ab wie bei der Vierfeldertafel mit absoluten Häufigkeiten.
2. Bekannte Häufigkeiten zuordnen
In diesem Schritt werden die absoluten Häufigkeiten in relative Häufigkeiten umgerechnet.
Gesamtzahl: 50
Kranke Studierende:
Studierende, die gestern eine Mütze getragen haben:
Studierende*r hatte gestern Mütze auf und ist heute erschienen, also gesund:
3. In die Vierfeldertafel einordnen
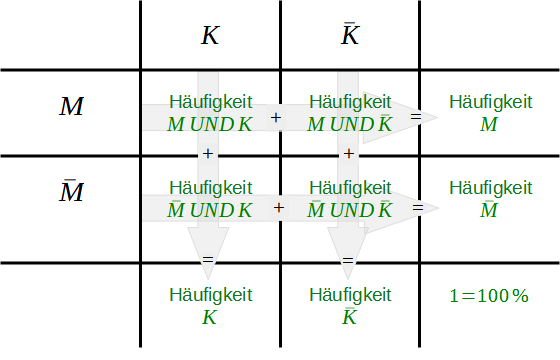
Die bekannten relativen Häufigkeiten werden nun in die Vierfeldertafel eingefügt. Im unteren rechten Kästchen steht nun nicht mehr die Gesamtzahl, sondern eine 1 bzw. 100%.
Beispiel | Allgemein |
|---|---|
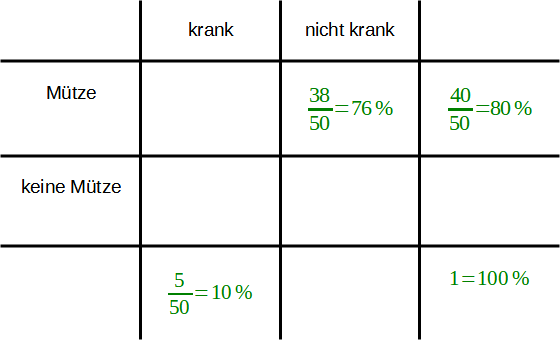 | 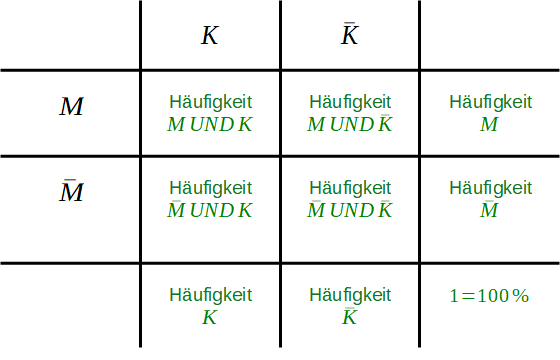 |
4. Restliche Felder ausrechnen
Die fehlenden Werte der Vierfeldertafel lassen sich ebenso wie bei der Vielfeldertafel mit absoluten Häufigkeiten über die Summen der Zeilen und Spalten berechnen.
Beispiel:
Beispiel | Allgemein |
|---|---|
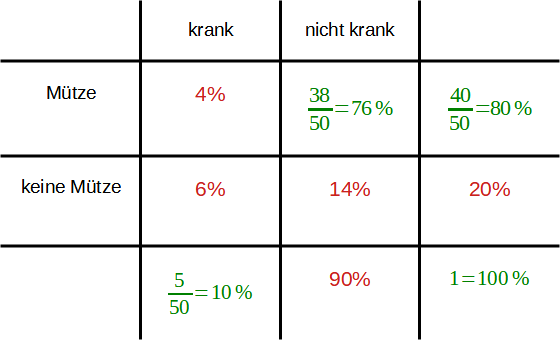 |  |
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
