Brennende Kerzen

Beide Kerze brennen langsam herunter. Da die rote Kerze deutlich dünner ist als die blaue, wird sie schneller kleiner. Am Anfang der Beobachtung ist die blaue Kerze cm und die rote cm hoch. Man hat bereits beobachtet, dass in einer Stunde die blaue um mm und die rote mm gleichmäßig herunterbrennt.
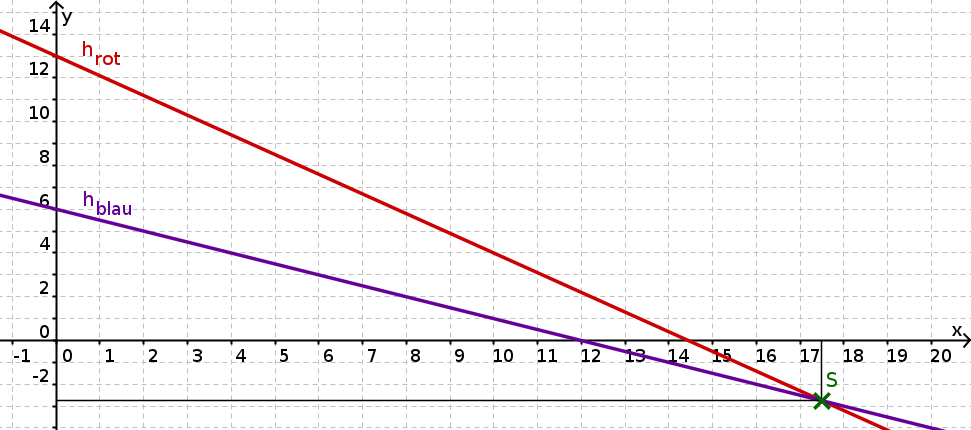
Stelle für beide Kerzen jeweils eine Funktionsgleichung auf, die die Höhe in Abhängigkeit der Zeit darstellt.
Berechne nun, nach wie vielen Stunden die Kerzen gleich lang sind, indem du die beiden Funktionen als Gleichungen mit den Variablen und auffasst.
Hinterfrage dein Ergebnis aus kritisch im Kontext der Aufgabe. An welcher Stelle gibt es ein Problem?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?