1 Aufgabe 2 - Lösung
Lösung Aufgabe
Überlege dir eine Funktion, die sicher einen Wendepunkt hat. Hierzu gibt es keine Musterlösung, sondern mehrere Möglichkeiten. Zum Beispiel hat die Funktion einen Wendepunkt bei . Diesen Punkt musst du jetzt noch so verschieben, dass der Wendepunkt bei ist.
ist eine mögliche Lösung.
Lösung Aufgabe
Überlege dir eine Funktion die entweder nur steigt oder nur fällt. Diese kannst du dann beliebig verändern, damit sie fallen und rechtsgekrümmt sind.
Beispiele sind und bzw .
ist linksgekrümmt und steigend.
Jetzt hast du die Möglichkeit den Graphen an den Achsen zu spiegeln. Spiegelst du ihn an der -Achse, ist er zwar fallen, aber immer noch linksgekrümmt. Spiegelst du den Graphen an der -Achse hast du eine Rechtskrümmung und der Graph fällt. Damit hast du es geschafft. Wie spiegelt man an der -Achse?
2 Aufgabe 3 - Aufgabenstellung
Diese Abbildung zeigt den Graphen der in definierten Funktion .
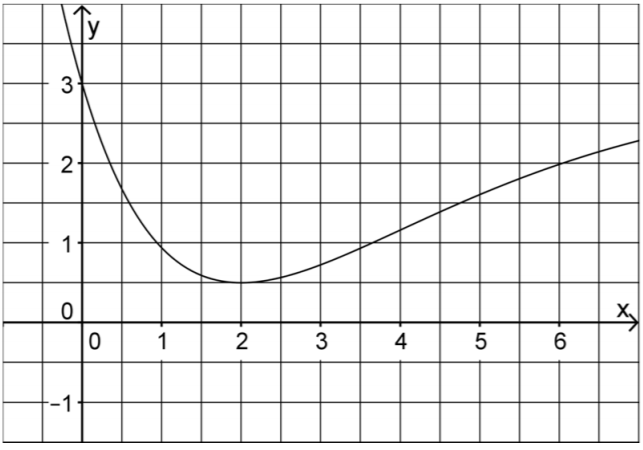
Bestimmen Sie mithilfe der Abbildung eine Näherungswert für . (2 BE)
Die Funktion ist die in definierte Stammfunktion von mit .
Geben Sie mit Hilfe der Abbildung einen Näherungswert für die Ableitung von an der Stelle an. (1 BE)
Zeigen Sie, dass mit gilt. (2 BE)
3 Aufgabe 3 - Lösung
Lösung Aufgabe
Die Größe des Integrals kannst du einfach ablesen, da eine Vorstellung zum Integral die Fläche unter der Kurve ist.
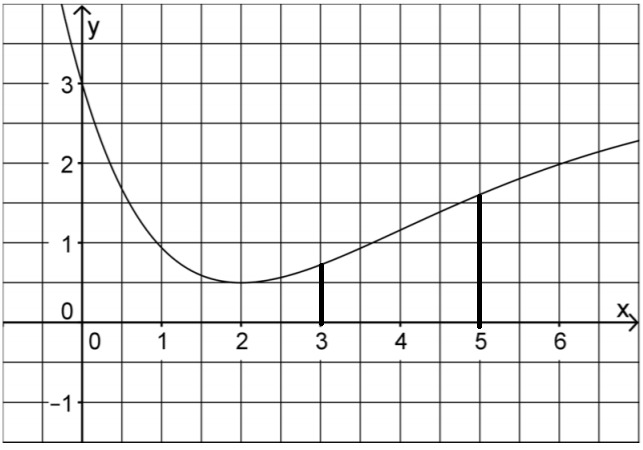
Zähle jetzt einfach die Kästchen, die von der Kurve, den zwei senkrechten Linien und der -Achse eingeschlossen sind. Kästchen zusammen geben eine Flächeneinheit ().
Ob du oder Kästchen heraus bekommst, ist bei einem Näherungswert nicht wichtig. Punkte gibt es trotzdem ;).
Lösung Aufgabe
Die Aufgabe ist einfach nur gemein gestellt und klingt total kompliziert. Ist es aber wirklich nicht! Was ist denn die Ableitung von der Stammfunktion ? Genau, einfach die Funktion . Deswegen musst du beim ablesen von diesem Punkt einfach nur in der Abbildung, die du schon gegeben hast, den Punkt mit der -Koordinate heraus suchen.
Bei ist da die Funktion die Ableitung der Stammfunktion ist.
Lösung Aufgabe
Überlege dir, wie du die Funktion integrierst. Dazu benötigst du die Stammfunktion. Diese hast du schon gegeben. Außerdem weißt du schon, dass . Aus dem Hauptsatz der Differential und Integralrechnung folgt:
Setze die gegebenen Grenzen aus der Aufgabenstellung ein.
Setze ein, was du schon weißt.
Und schon bist du fertig! :)
4 Aufgabe 4 - Aufgabenstellung
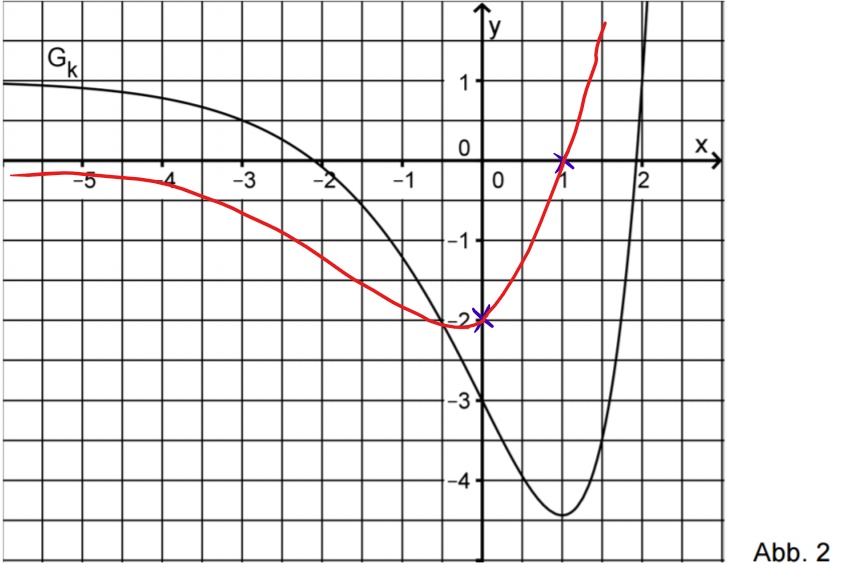
Abbildung zeigt den Graphen einer in definierten Funktion . Skizzieren Sie in Abbildung den Graphen der zugehörigen Ableitungsfunktion . Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen an dessen Wendepunkt sowie die Nullstelle von . (4 BE)
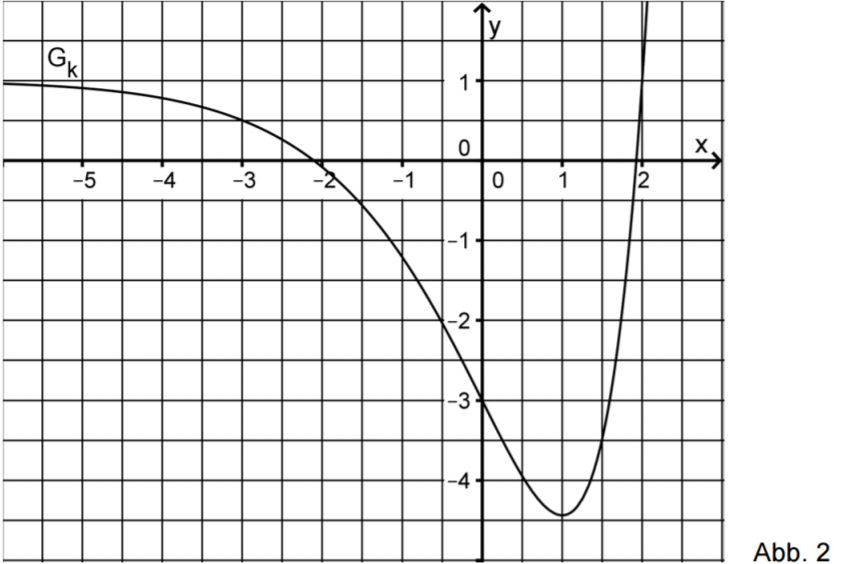
5 Aufgabe 4 - Lösung
Um den Ableitungsgraphen zeichnen zu können, benötigst du:
Extremstellen der Funktion
Monotonieverhalten der Funktion
Verhalten im Unendlichen
Die Extremstelle von ist . bei hat die Ableitung eine Nullstelle.
Die Extremstelle ist ein Minimum links der Extremstelle fällt die Funktion (Ableitungsgraph unterhalb der -Ache) und rechts der Extremstelle steigt die Funktion (Ableitungsfunktion oberhal der -Achse)
Der Wendepunkt ist die Nullstelle der zweiten Ableitung und somit die Extremstelle der Ableitung.
Die Steigung am Wendepunkt beträgt ungefähr .
Daraus ergibt sich folgende Skizze: