Ähnlich wie sich ein Stück Stoff in verschiedene Richtungen dehnen lässt, lässt sich ein Funktionsgraph in x- und y-Richtung stauchen und strecken.
Das Strecken bzw. Stauchen eines Funktionsgraphen kann man sich folgendermaßen vorstellen:
Der Graph ist auf einem elastischen Stoff gezeichnet. In -Richtung strecken heißt, den Stoff nach oben und unten zu ziehen, in -Richtung strecken heißt entsprechend, den Stoff nach links und rechts zu ziehen.
Um den Graphen zu stauchen, "schiebt" man den Stoff zusammen (ohne dass er Falten wirft).
Diese Änderung kann man auch mathematisch am Funktionsterm darstellen.
Streckungs- bzw. Stauchungsfaktor
Wenn die Funktion in -Richtung getreckt oder gestaucht werden soll, multipliziert man den Funktionsterm mit einem Faktor . Wenn die Funktion in -Richtung gestreckt oder gestaucht werden soll, dividiert man die Variable durch .
Ist spricht man von Stauchen,
ist von Strecken.
Beispiele
Streckungsfaktor (oft auch Streckfaktor genannt)
Streckungsfaktor (oft auch Streckfaktor genannt)
Streckung und Stauchung in -Richtung
Im Folgenden ist der Graph der Ausgangsfunktion rot eingezeichnet und der gestreckte bzw. gestauchte Graph der neuen Funktion schwarz.
Soll in -Richtung gestreckt (gestaucht) werden, wird der ganze Funktionsterm mit dem Faktor multipliziert:
Streckfaktor | ||
|---|---|---|
Funktionsterm d. veränderten Funktion | ||
Geometrische Veränderung | Stauchung | Streckung |
Graphen | 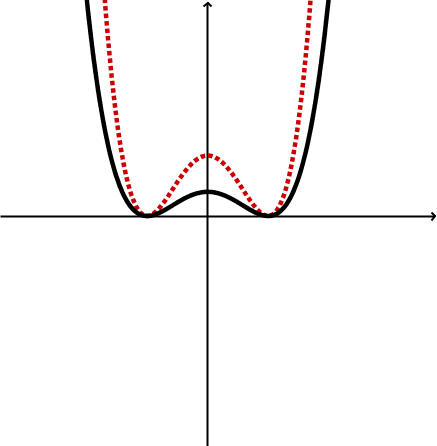 | 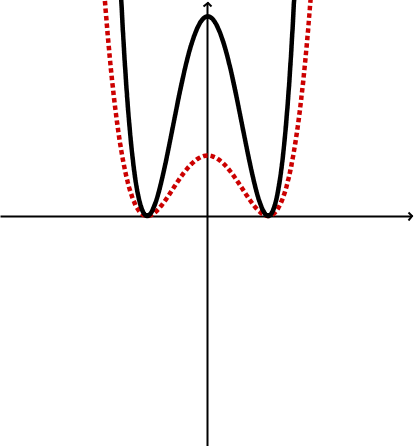 |
Falls negativ ist, so wird der Graph zusätzlich noch an der -Achse gespiegelt.
Streckfaktor | ||
|---|---|---|
Funktionsterm d. veränderten Funktion | ||
Geometrische Veränderung | Spiegelung an der x-Achse Streckung | Spiegelung an der x-Achse Stauchung |
Graphen | 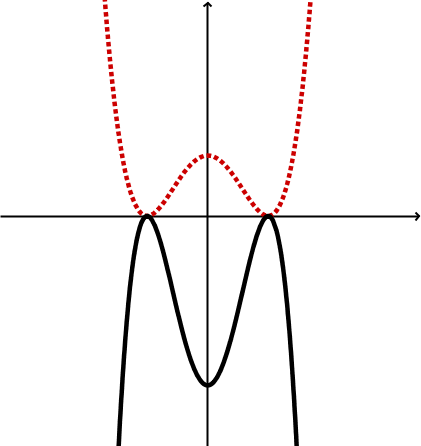 | 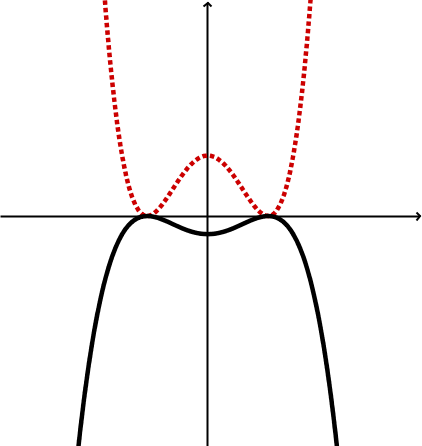 |
Veranschaulichung am Applet
Stauchung und Streckung in -Richtung
Wie oben ist auch hier der Ausgangsgraph rot eingezeichnet und der gestreckte (gestauchte) Graph schwarz.
Soll in -Richtung gestreckt (gestaucht) werden, wird die Variable durch den Faktor dividiert.
Streckfaktor | ||
|---|---|---|
Funktionsterm d. veränderten Funktion | ||
Geometrische Veränderung | Stauchung | Streckung |
Graphen | 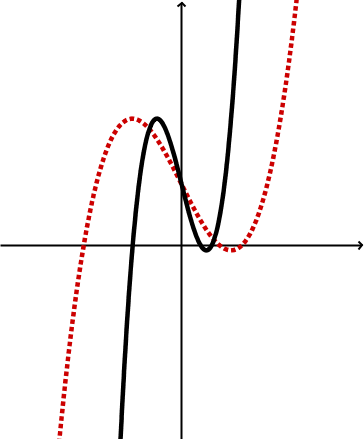 | 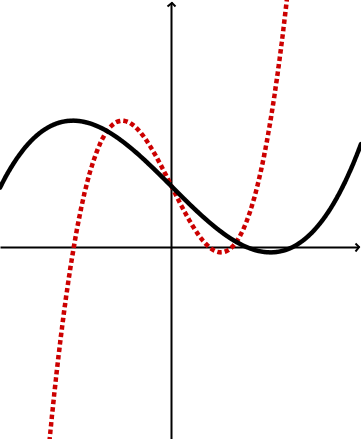 |
Streckfaktor | ||
|---|---|---|
Funktionsterm d. veränderten Funktion | ||
Geometrische Veränderung | Spiegelung an der y-Achse | Spiegelung an der y-Achse Stauchung |
Graphen | 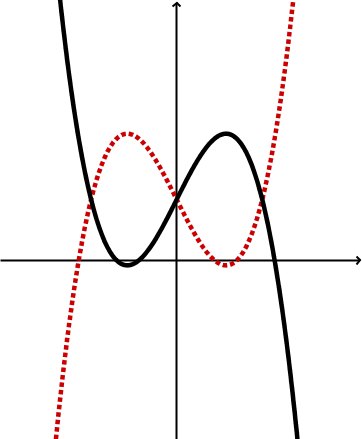 | 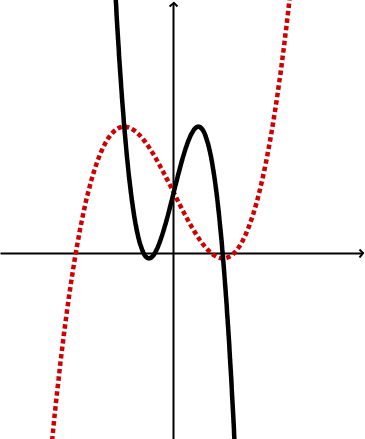 |
Veranschaulichung am Applet
Video zur Streckung von Funktionsgraphen
Laden
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Verändern von Funktionsgraphen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
