Von einer Raute kennst du die Fläche und die Länge der Diagonalen . Wie lang ist die Diagonale ?
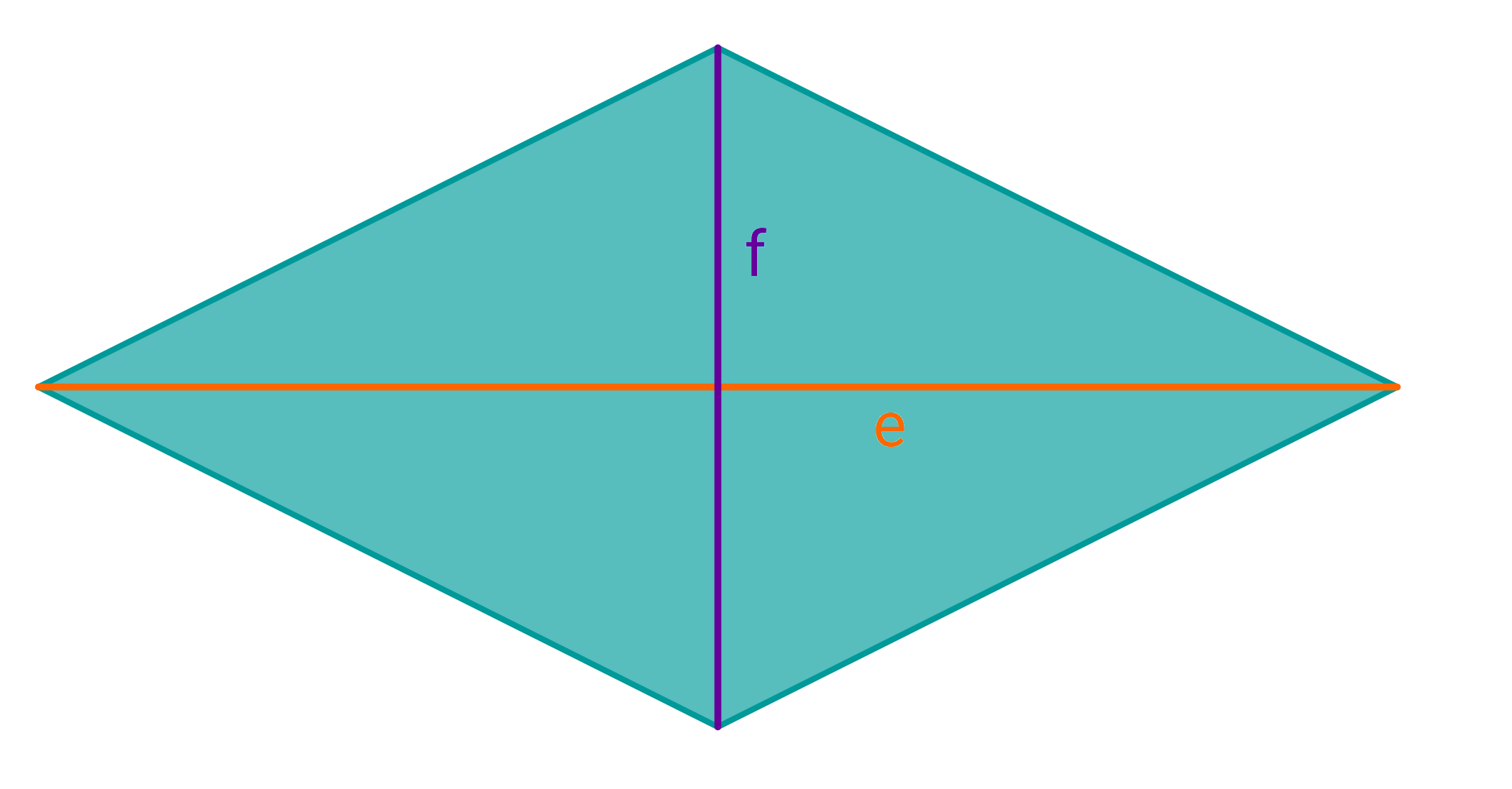
cm
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Von einer Raute kennst du die Fläche und die Länge der Diagonalen . Wie lang ist die Diagonale ?
