Ein Quadrat und ein Kreis haben denselben Flächeninhalt.
Der Radius vom Kreis beträgt . Wie groß ist die Seitenlänge des Quadrats?
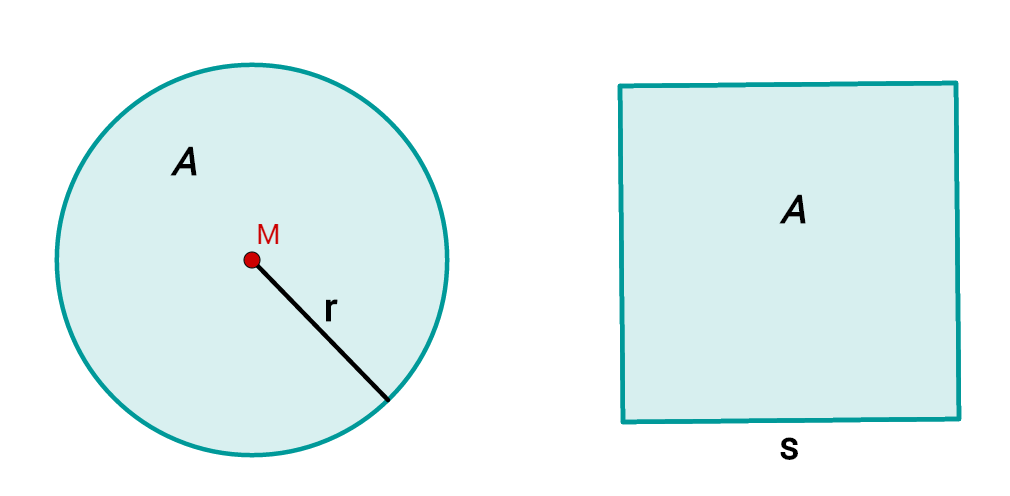
cm
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Ein Quadrat und ein Kreis haben denselben Flächeninhalt.
Der Radius vom Kreis beträgt . Wie groß ist die Seitenlänge des Quadrats?
