Berechne für die nebenstehende Figur den Winkel , wenn .
Die Punkte liegen auf dem Halbkreis.
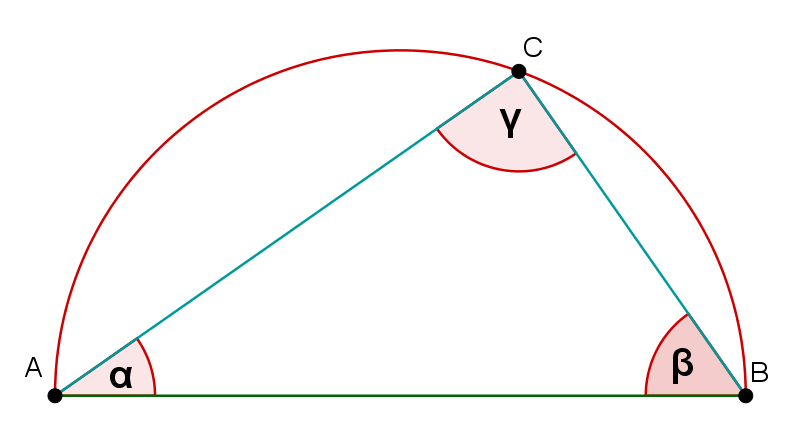
°
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Berechne für die nebenstehende Figur den Winkel , wenn .
Die Punkte liegen auf dem Halbkreis.
