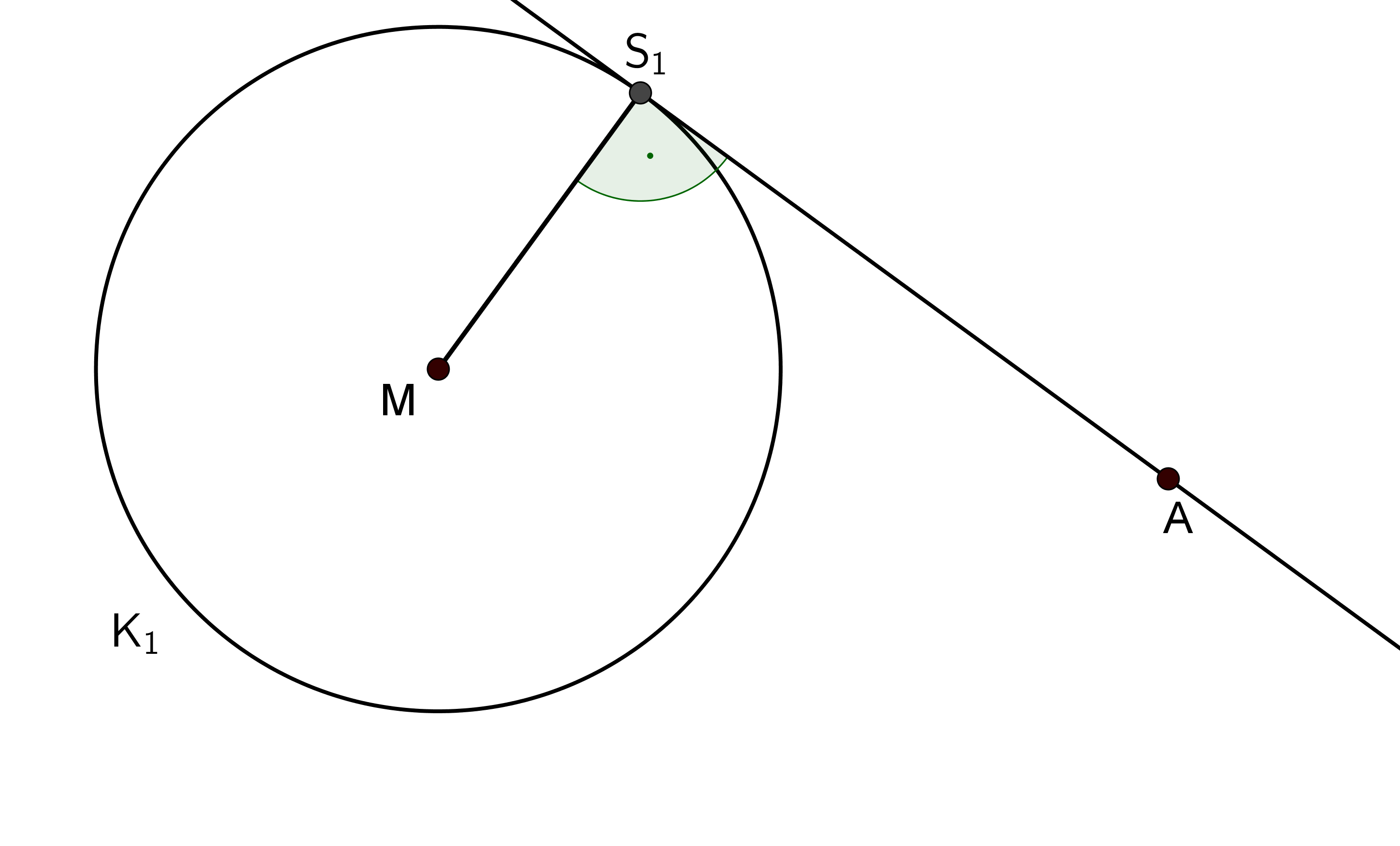
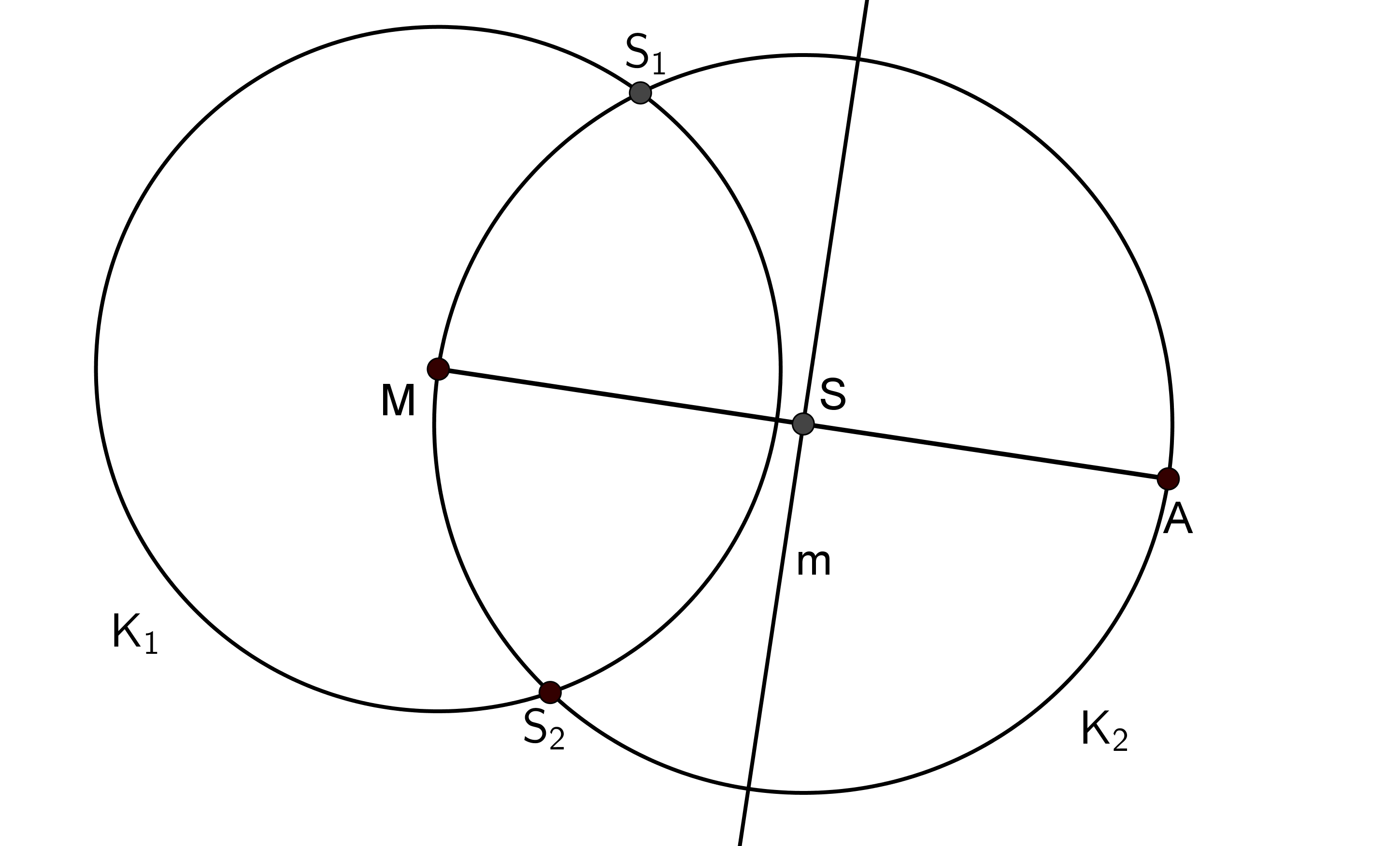
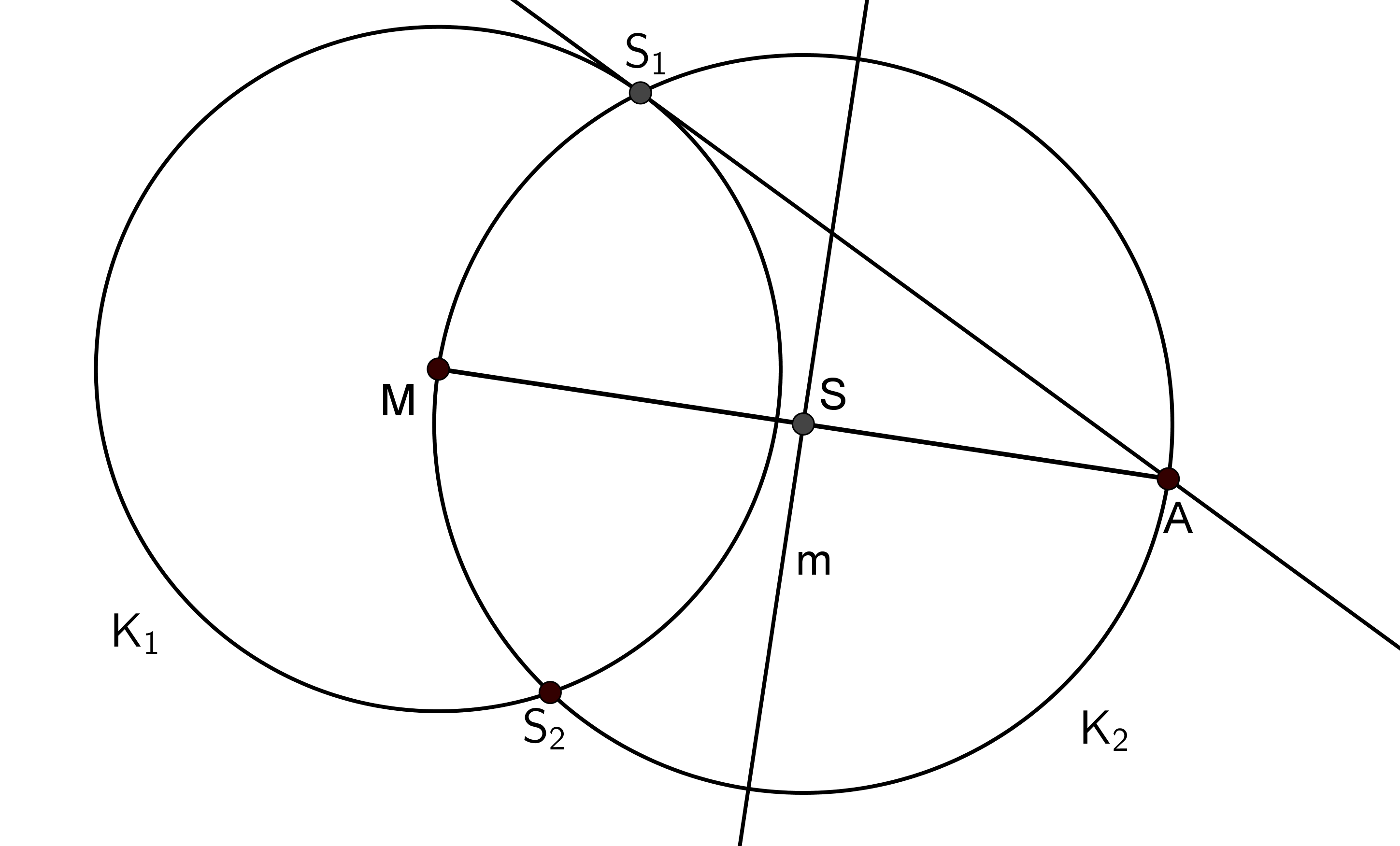
Gegeben ist - wie in nebenstehender Abbildung dargestellt - der Kreis mit Mittelpunkt und ein Punkt , der außerhalb des Kreises liegt.
Konstruiere eine Tangente des Kreises durch den Punkt .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?