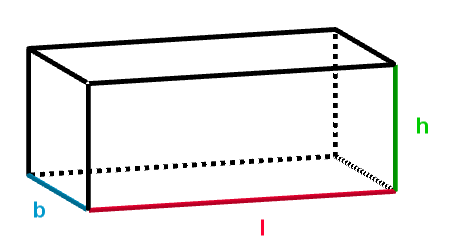
1 Volumen eines Quaders
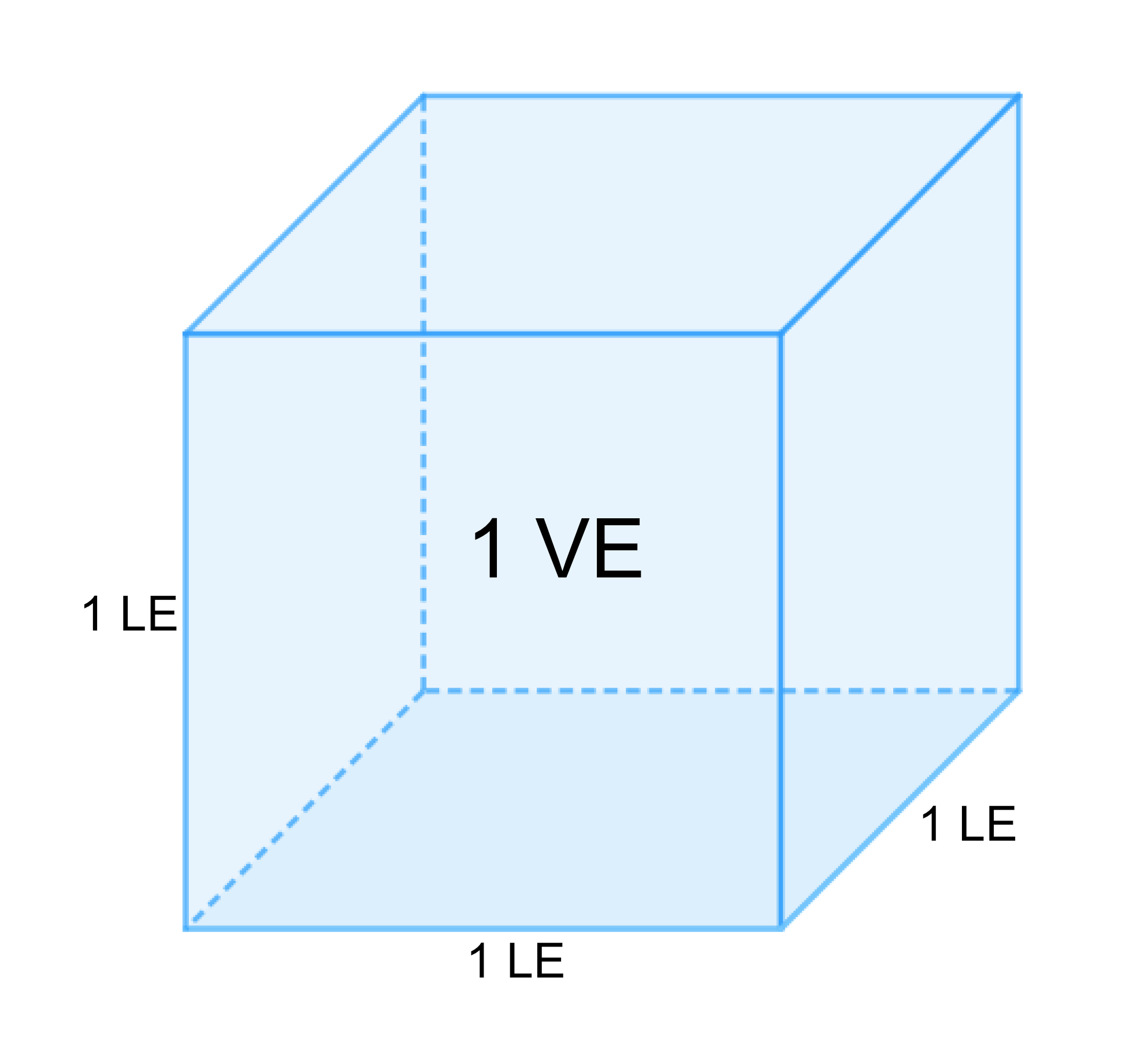
Ein Würfel mit dem Rauminhalt einer Volumeneinheit (1 VE) wird als Einheitswürfel bezeichnet. Er ist 1 LE breit, lang und hoch. Der Einheitswürfel hat beispielsweise ein Volumen von und ist breit, lang und tief.
Mithilfe der Einheitswürfel lässt sich das Volumen eines Quaders bestimmen. Dafür legst du so viele Einheitswürfel in den Quader wie möglich und zählst die Anzahl der Würfel ab.
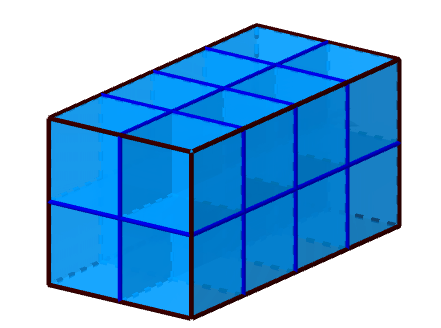
Ein mit Einheitswürfeln ausgelegter Quader sieht beispielsweise so aus:
Das Volumen des Quaders beträgt so viele VE wie es Einheitswürfel im Quader gibt, hier z.B. 16 VE.
2 Übungsaufgaben
Laden
3 Zusammenfassung
Beim Zählen der Einheitswürfel könnte dir aufgefallen sein, dass man die Anzahl der Würfel schnell durch eine Multiplikation lösen kann.
Die Anzahl der Einheitswürfel berechnest du wie folgt:
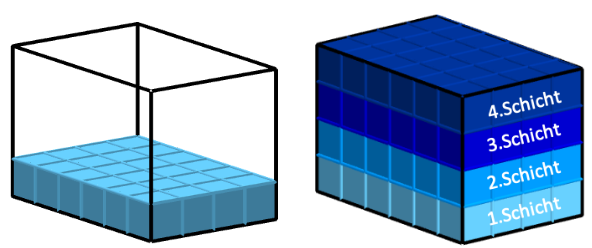
Die Anzahl der Einheitswürfel in einer Schicht wiederum ergibt sich aus der Anzahl der Einheitswürfel in einer Reihe mal der Anzahl der Reihen.
Die Anzahl der Einheitswürfel in einer Reihe entspricht der
Die Anzahl der Reihen entspricht der
Die Anzahl der Schichten entspricht der
4 Teste dein Wissen!
(Lückentextaufgabe)
Um das Volumen eines Quaders zu bestimmen, legst du den Quader mit [Einheitswürfeln] aus. Diese haben ein Volumen von [1 VE]. Eine mögliche Volumeneinheit ist beispielsweise []. Die Anzahl der Einheitswürfel kannst du abzählen oder durch [Multiplikation] der Länge, Breite und Höhe des Quaders berechnen. Ein Quader mit der Länge , Breite und Höhe von hat also ein Volumen von [].
[\Einheitsquader] [\1FE] [\1LE] [\Addition] \[] [\] [] [ VE] [\ VE]