NRW MSA 2021 Teil 2 - Aufgabe 1: Glaskugeln
Ein Unternehmen stellt lackierte Glaskugeln her (Abbildung 1).
Die Glaskugeln haben einen Durchmesser von .

Abbildung 1: Glaskugel
Berechne das Volumen einer Glaskugel.
Nach der Herstellung der Form wird die Kugeloberfläche lackiert.
Mit einem Liter Farbe kann eine Fläche von lackiert werden. Berechne, wie viele Glaskugeln mit einem Liter Farbe lackiert werden können. (4 P)
GlaskugelnEin Praktikant behauptet: „Für eine Glaskugel mit doppeltem Durchmesser benötigt man viermal so viel Farbe.“
Hat der Praktikant recht? Begründe.
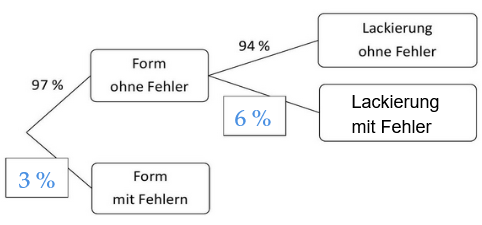
Bevor die lackierten Glaskugeln verpackt werden, durchlaufen sie eine Qualitätskontrolle. Zuerst wird die Form, danach die Lackierung auf Fehler kontrolliert. Alle Glaskugeln mit einem Fehler werden direkt aussortiert. Das Baumdiagramm zeigt die Anteile. Die Anteile werden im Folgenden als Wahrscheinlichkeiten gedeutet. (2 P)
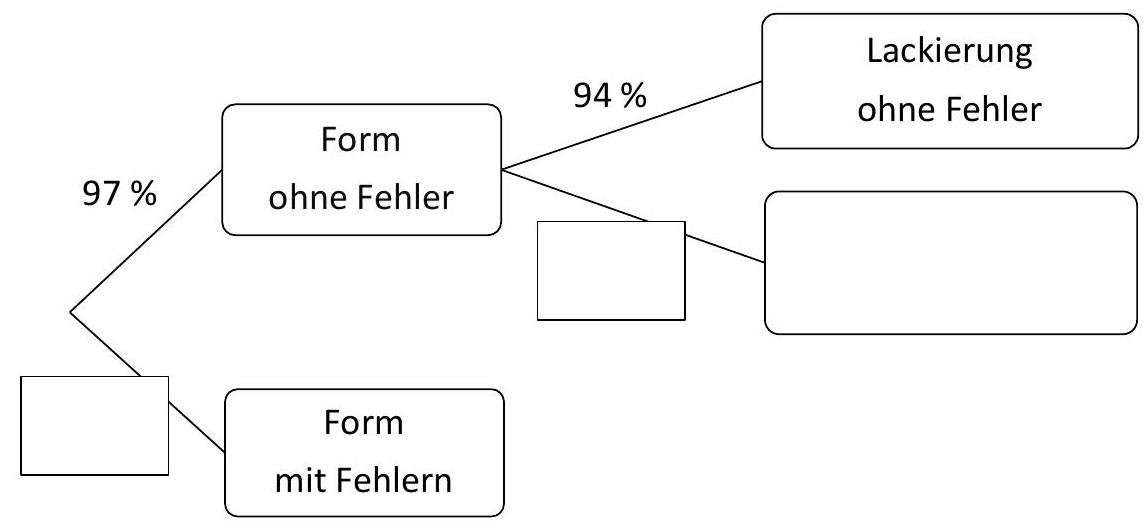
Ergänze die drei fehlenden Angaben im Baumdiagramm.
Begründe, warum der untere Ast des Baumdiagramms nicht fortgeführt ist. (2 P)
Insgesamt werden 2 000 Glaskugeln kontrolliert. Berechne, wie viele fehlerfreie Glaskugeln zu erwarten sind. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?