Abbildungen im Raum mithilfe von Matrizen (1)

1. Projektion auf eine Ebene:

Ein beliebiger Punkt $P$ wird auf eine gegebene Ebene $E$ projiziert.

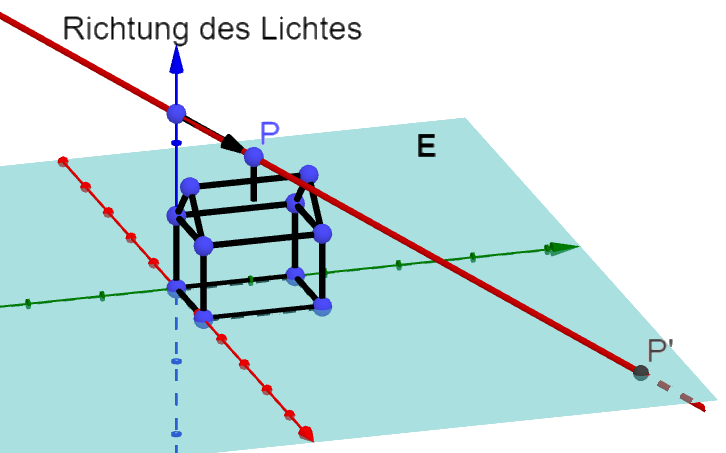
a) Bestimmung der Projektionsmatrix für eine Projektion in die $x_{1} x_{2}$ -Ebene

Ein typisches Beispiel:

Der Schattenwurf eines gegebenen Punktes $P$ (z.B. Schornstein eines Hauses, siehe Abbildung)

auf eine gegebene Ebene $E$ .

Gleichung der Ebene $E : x_{3} = 0$

Richtung der Sonnenstrahlen: $\vec{v} = (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

Ein beliebiger Punkt des Hauses: $P (a | b | c)$

Gesucht wird zum Punkt $P$ des Hauses der Bildpunkt $P^{'}$ des Schattens in der Ebene $E$ .

Erstelle die Gleichung einer Hilfsgeraden $h$ durch $P$ mit der Richtung $\vec{v}$ .

$h : \vec{x} = (\begin{array}{c} a \\ b \\ c \end{array}) + r \cdot (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

Die Hilfsgerade $h$ wird mit der Ebene $E$ geschnitten.

$h \cap E$ :

$z = 0 \Rightarrow c + r \cdot v_{3} = 0 \Rightarrow r = - \frac{c}{v_{3}}$

Der Wert für $r$ wird in $h$ eingesetzt und man erhält die Koordinaten von $P^{'}$ .

${\vec{x}}_{P^{'}} = (\begin{array}{c} a \\ b \\ c \end{array}) - \frac{c}{v_{3}} \cdot (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array}) = (\begin{array}{c} a - c \cdot \frac{v_{1}}{v_{3}} \\ b - c \cdot \frac{v_{2}}{v_{3}} \\ 0 \end{array})$ $\Rightarrow P^{'} (a - c \cdot \frac{v_{1}}{v_{3}} | b - c \cdot \frac{v_{2}}{v_{3}} | 0)$

Die Projektion in die Ebene $E$ kann auch durch eine $3 x 3$ Matrix $A$ beschrieben werden.

Es ist:

$(\begin{array}{c} a - c \cdot \frac{v_{1}}{v_{3}} \\ b - c \cdot \frac{v_{2}}{v_{3}} \\ 0 \end{array}) = (\begin{array}{ccc} 1 & 0 & - \frac{v_{1}}{v_{3}} \\ 0 & 1 & - \frac{v_{2}}{v_{3}} \\ 0 & 0 & 0 \end{array}) \cdot (\begin{array}{c} a \\ b \\ c \end{array}) \Rightarrow A_{x_{1} x_{2}} = (\begin{array}{ccc} 1 & 0 & - \frac{v_{1}}{v_{3}} \\ 0 & 1 & - \frac{v_{2}}{v_{3}} \\ 0 & 0 & 0 \end{array})$

Die Matrix $A_{x_{1} x_{2}}$ ist die Projektionsmatrix.

Alle Punkte des Raumes werden mit der Matrix $A_{x_{1} x_{2}}$ in die Ebene $E_{x_{1} x_{2}}$ abgebildet.

MerkeProjektion auf eine Ebene E

Es gilt:

Jeder Bildpunkt $P^{'}$ liegt in der Ebene $E$ .
Alle Punkte der Ebene sind sogenannte Fixpunkte, d.h. es sind Punkte, die bei einer Abbildung auf sich selbst abgebildet werden.
Bei einer Projektion in die Ebene $E$ gilt immer: $A \cdot A = A$

b) Bestimmung der Projektionsebene

Gegeben ist eine Projektionsmatrix (Nachweis mit der Beziehung $A \cdot A = A$ ),

z.B. die Matrix $A = (\begin{array}{ccc} 1 & 0 & - \frac{v_{1}}{v_{3}} \\ 0 & 1 & - \frac{v_{2}}{v_{3}} \\ 0 & 0 & 0 \end{array})$

Gesucht ist die Ebene, die die Fixpunkte enthält, d.h. die Ebene, in die projiziert wird.

Fixpunktgleichung: $A \cdot \vec{x} = \vec{x}$

$(\begin{array}{ccc} 1 & 0 & - \frac{v_{1}}{v_{3}} \\ 0 & 1 & - \frac{v_{2}}{v_{3}} \\ 0 & 0 & 0 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array})$

Man erhält drei Gleichungen:

$(I) : x_{1} - \frac{v_{1}}{v_{3}} \cdot x_{3} = x_{1} \Rightarrow - \frac{v_{1}}{v_{3}} \cdot x_{3} = 0 \Rightarrow x_{3} = 0$

$(I I) : x_{2} - \frac{v_{2}}{v_{3}} \cdot x_{3} = x_{2} \Rightarrow - \frac{v_{2}}{v_{3}} \cdot x_{3} = 0 \Rightarrow x_{3} = 0$

$(I I I) : 0 = x_{3}$

Also dreimal die Gleichung $x_{3} = 0$ .

Das ist die gesuchte Ebenengleichung $E$ , in die projiziert wird.

c) Bestimmung der Projektionsrichtung

Man wählt einen beliebigen Punkt im Raum, z.B. den Punkt $Q$ mit den Koordinaten $(q_{1} | q_{2} | q_{3})$ und projiziert ihn mit der Matrix $A$ in die Ebene $E$ , d.h. man erhält den Bildpunkt $Q^{'} .$

$(\begin{array}{ccc} 1 & 0 & - \frac{v_{1}}{v_{3}} \\ 0 & 1 & - \frac{v_{2}}{v_{3}} \\ 0 & 0 & 0 \end{array}) \cdot (\begin{array}{c} q_{1} \\ q_{2} \\ q_{3} \end{array}) = (\begin{array}{c} q_{1} - \frac{v_{1}}{v_{3}} \cdot q_{3} \\ q_{2} - \frac{v_{2}}{v_{3}} \cdot q_{3} \\ 0 \end{array}) \Rightarrow \vec{O Q^{'}} = (\begin{array}{c} q_{1} - \frac{v_{1}}{v_{3}} \cdot q_{3} \\ q_{2} - \frac{v_{2}}{v_{3}} \cdot q_{3} \\ 0 \end{array})$

Die Projektionsrichtung ist der Vektor $\vec{Q Q^{'}} = \vec{O Q^{'}} - \vec{O Q} = (\begin{array}{c} q_{1} - \frac{v_{1}}{v_{3}} \cdot q_{3} \\ q_{2} - \frac{v_{2}}{v_{3}} \cdot q_{3} \\ 0 \end{array}) - (\begin{array}{c} q_{1} \\ q_{2} \\ q_{3} \end{array}) = (\begin{array}{c} - \frac{v_{1}}{v_{3}} \cdot q_{3} \\ - \frac{v_{2}}{v_{3}} \cdot q_{3} \\ - q_{3} \end{array}) = - \frac{q_{3}}{v_{3}} \cdot (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

Die Projektionsrichtung ist also der Vektor $\vec{v} = (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$ .

d) Die Projektionsmatrix für eine Projektion in die $x_{2} x_{3}$ -Ebene

$A_{x_{2} x_{3}} = (\begin{array}{ccc} 0 & 0 & 0 \\ - \frac{v_{2}}{v_{1}} & 1 & 0 \\ - \frac{v_{3}}{v_{1}} & 0 & 1 \end{array})$

e) Die Projektionsmatrix für eine Projektion in die $x_{1} x_{3}$ -Ebene

$A_{x_{1} x_{3}} = (\begin{array}{ccc} 1 & - \frac{v_{1}}{v_{2}} & 0 \\ 0 & 0 & 0 \\ 0 & - \frac{v_{3}}{v_{2}} & 1 \end{array})$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?